Математика — 5
Конгруэнтные фигуры
Конгруэнтные фигуры — это фигуры, имеющие одинаковую форму и равные размеры. Если при наложении друг на друга все точки одной фигуры совпадают с соответствующими точками другой, то эти фигуры конгурэнтные. Эти фигуры называют также равными. Конгруэнтность фигур обозначается знаком “≅”. Отрезок AB конгруэнтен(равен) отрезку CD. AB ≅ CD Длина каждого отрезка равна 2 см. Угол EFG конгруэнтен
(равен) углу LMN.
∠EFG ≅ ∠LMN
Квадрат KLMN конгруэнтен (равен) квадрату OPRS. Стороны обоих квадратов равны друг другу и составляют 15 мм, а углы прямые. KLMN ≅ OPRS. Чтобы показать, что стороны и углы фигуры конгруэнтны, их перечёркивают короткими черточками.
- Начертите в тетради фигуры, показанные на рисунке. Назовите их. Отметьте равные стороны и углы.
- Вырежьте из цветной бумаги различные фигуры. Нарисуйте конгруэнтные им фигуры, обведя вырезанные фигуры чёрным контуром на белом листе.
-
Конгруэнтность фигур можно проверить двумя способами.
1) Вырезать одну из фигур, и наложить её на другую.
2) Измернием и сравнением сторон и углов фигур.
На рисунке даны треугольники
ΔABC ≅ ΔDEF. Нарисуйте эти треугольники в тетради. На сторонах и углах надпишите их размеры. -
Какие две фигуры являются конгруэнтными?
1)
2)
4)
5)
6)
Конгруэнтное и подобное: разница и сравнение
«Конгруэнтный» и «Подобный» — это термины, которые обычно используются в математических концепциях форм, размеров и фигур.
Языковая викторина
Языковой тест помогает нам улучшить наши языковые навыки
1 / 10
Как называется слово или фраза, имеющая несколько значений?
полисема
омофон
омоним
Синоним
2 / 10
Как называется изучение используемого языка и контекста?
Прагматика
Grammar
Семантика
Лексикология
3 / 10
Как называется язык, состоящий из символов, которые представляют идеи или объекты?
Язык знаков
Вербальный язык
Письменный язык
Язык тела
4 / 10
Каким термином обозначают слова, заменяющие существительные?
Местоимение
Наречие
Имя прилагательное
конъюнкция
5 / 10
В чем разница между синтаксисом и семантикой?
Синтаксис — это грамматика, семантика — это значение
Синтаксис — это значение, семантика — это грамматика.
Синтаксис — это произношение, семантика — это значение
Синтаксис — это словарный запас, семантика — это грамматика.
6 / 10
Какое слово описывает существительное?
Местоимение
Наречие
Имя прилагательное
конъюнкция
7 / 10
Кто является ответственным лицом в средней школе?
Принцип
Основной
принцпал
8 / 10
Выберите слово, которое означает то же, что и «неуместно»:
Терять
Найти
Прятаться
Покрывать
9 / 10
Ахмед 65 кг, а Али 50 кг, поэтому Ахмед _ _ _ _ _ _ Али.
Тяжелее чем
Тяжелее, чем
Тяжелый, как
тяжелее
10 / 10
Какой язык имеет наибольшее количество носителей?
Хинди
Испанский
Английский
Китайский мандарин
ваш счет
Конгруэнтные фигуры имеют одинаковую структуру, размер и форму и могут быть полностью наложены друг на друга.
Подобные фигуры выглядят одинаково по форме, но не имеют точных размеров, как другая фигура.
Конгруэнтное против подобногоОсновные выводы
- Конгруэнтные фигуры имеют одинаковый размер и форму; подобные фигуры имеют одинаковую форму, но могут отличаться по размеру.
- Конгруэнтные формы можно накладывать друг на друга; подобные формы могут быть изменены или масштабированы, чтобы соответствовать друг другу.
- И конгруэнтные, и подобные фигуры имеют одинаковые углы, но конгруэнтные формы имеют одинаковую длину сторон, в то время как аналогичные формы имеют пропорциональные длины сторон.
Конгруэнтные фигуры идентичны по форме и размеру, а это означает, что они могут идеально накладываться друг на друга. Подобные формы, с другой стороны, имеют одинаковую форму, но могут отличаться по размеру, сохраняя те же пропорции, но не обязательно одинаковые размеры.
Конгруэнтные фигуры могут иметь или не иметь одинаковую ориентацию размещения в целом или в 3D, в то время как аналогичные фигуры не могут иметь одинаковое расположение или экспозицию.
Конгруэнтные фигуры — это точные геометрические фигуры, которые можно размещать и вращать, чтобы накладывать друг на друга и создавать копии.
Тем не менее, похожие фигуры не могут повторять друг друга, потому что они неравны по размеру.
Сравнительная таблица
| Параметры сравнения | конгруэнтный | Аналогичный |
|---|---|---|
| Определение | Конгруэнтность — это термин, который относится к фигурам или вообще к чему-либо, что одинаково по размеру и форме и может накладываться друг на друга. | Подобные используются для фигур или других вещей, которые похожи друг на друга по размеру и форме, но не идентичны по размерам. |
| Принцип | Конгруэнтные фигуры обычно следуют математическому принципу теоремы SSS, где измерения всех сторон и углов у двух фигур одинаковы. | Подобные или идентичные фигуры не подчиняются никакому такому правилу. Формы, стороны и углы двух фигур могут различаться. |
| Точность | Конгруэнтные фигуры — это геометрически точные и накладывающиеся друг на друга фигуры. | Подобный — это свободный термин для обозначения идентичных фигур, которые во многом похожи друг на друга по форме. |
| ориентация | Конгруэнтные фигуры накладываются друг на друга, даже если они расположены в разных ориентациях. Это можно сделать, вращая статистику. | Подобные фигуры не накладываются друг на друга, даже если они расположены в одной ориентации. |
| Множественность значений | Congruent также может использоваться как прилагательное для описания объектов или переживаний, которые могут накладываться друг на друга или совпадать. | Аналогичный также может использоваться в качестве прилагательного для описания вещей или объектов, связанных из-за их схожей природы. Он также используется для сравнения. |
Что означает термин конгруэнтность?
Конгруэнтность — это термин, используемый для обозначения фигур, форм, объектов или всего, что имеет одинаковые измерения формы и размера.
Эти фигуры полностью накладываются друг на друга из-за их одинакового размера и меры.
Это точные математические и геометрические фигуры, которые следуют теореме SSS (сторона, сторона, сторона), что означает, что все стороны и углы у них равны.
Эти фигуры можно накладывать друг на друга, даже в разных ориентациях, или размещать, просто вращая их до тех пор, пока они не совпадут.
Конгруэнтные фигуры идентичны по размерам и используют понятия точности в математическом мире.
Термин «конгруэнтность» можно использовать по-разному. В некоторых случаях оно используется как прилагательное для точного описания объектов или переживаний, которые накладываются друг на друга или совпадают.
Он также может определять мотивационные или неразрывно связанные идеалы и принципы людей.
Что подразумевается под термином «подобный»?
Аналогично свободный термин, используемый для обозначения фигур, которые выглядят одинаково по форме и размеру.
Эти фигуры не накладываются друг на друга, потому что они не равны по размерам.
Таким образом, эти фигуры не производят реплики друг друга.
Подобные фигуры не следуют математическим понятиям или принципам, потому что они не равны по размеру или форме.
Эти цифры можно использовать для сравнения или для получения приблизительного представления о формах и размерах.
Они не накладываются друг на друга и никогда не совпадают с ориентацией размещения друг друга.
Термин «аналогичный» также может использоваться в нескольких контекстах. Оно используется как прилагательное для сравнения или связывания объектов или переживаний аналогичного характера.
Сходство не является точным понятием, но помогает человеку получить краткий намек на принципы и идеалы, связанные друг с другом.
Основные различия между конгруэнтным и подобным
- Конгруэнтные — это термин, используемый для фигур или форм, которые идентичны друг другу с точки зрения формы и размера, тогда как похожие — это термин, который относится к фигурам, которые выглядят одинаково, но не имеют одинаковых размеров.
- Конгруэнтность — это точный термин, который обычно используется для идентичных и геометрических фигур, тогда как аналог — это термин, который используется для получения общего представления о статистике.
- Концепция конгруэнтных фигур следует жестким математическим принципам и теоремам, тогда как подобные фигуры не следуют никаким таким изображениям.
- Конгруэнтные фигуры накладываются друг на друга и могут создавать копии, тогда как подобные фигуры не могут накладываться друг на друга.
- Термин конгруэнтный может использоваться как прилагательное для обозначения совпадающих и наложенных друг на друга инцидентов, тогда как аналогичный используется для определения опыта или объектов аналогичной природы.
Рекомендации
- https://study.com/academy/lesson/similar-figures-definition-examples.htm
- lhttps://dictionary.cambridge.org/dictionary/english/congruent
Один запрос?
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы предоставить вам ценность. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/родными. ДЕЛИТЬСЯ ♥️
Эмма Смит
Эмма Смит имеет степень магистра английского языка в колледже Ирвин-Вэлли.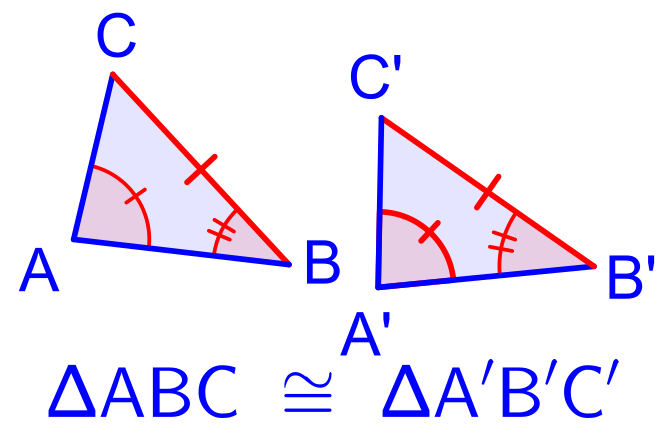
Она работает журналистом с 2002 года, пишет статьи об английском языке, спорте и праве. Подробнее обо мне на ней био страница.
Каковы примеры конгруэнтных треугольников в реальной жизни?
Амина РешмаЧтение за 4 мин.
Что такое конгруэнтность?
Конгруэнтность относится к двум фигурам или объектам, которые являются точными копиями друг друга. Конгруэнтные фигуры перекрываются точка-точка, когда они сложены одна поверх другой. Даже если фигуры могут находиться в разных плоскостях, они все равно будут конгруэнтными, если их стороны, площади покрытия и объем одинаковы. 1
Значение конгруэнтности
Построение нашего понимания структур требует изучения конгруэнтности в цифрах. Благодаря развитию пространственного интеллекта вы можете иногда обнаружить две структуры, предметы или продукты, полностью идентичные друг другу.
Конгруэнтные фигуры — это понятие, которое лучше понимается с одинаковым интеллектом.
Концепция конгруэнтности полезна в области архитектуры, ландшафтного дизайна, моделирования продуктов и производства для бизнеса. Помимо практической пользы, конгруэнтность укрепляет основу учащихся и помогает им сформировать более гибкое понимание понятий площади и объема. На уроке геометрии мы сравниваем две фигуры и сталкиваемся с конгруэнтностью, точно так же, как мы читаем о равенстве чисел на уроке элементарной математики. 1
Что такое треугольник?
Одной из первых фигур, которую мы изучаем, является треугольник. Треугольник — это двумерная фигура с тремя сторонами, тремя углами и тремя вершинами. 2 Треугольники представляют собой трехсторонние замкнутые фигуры, которые можно разделить на различные типы в зависимости от их сторон и углов. Равнобедренные треугольники, равнобедренные треугольники и разносторонние треугольники являются распространенными вариантами.
Итак, что же тогда такое конгруэнтный треугольник?
Конгруэнтные треугольники — это треугольники, у которых три стороны и три угла совпадают с соответствующими сторонами и углами другого треугольника. Другими словами, мы можем сказать, что конгруэнтные треугольники имеют равные соответствующие стороны и углы. Чтобы треугольники выглядели одинаково, их можно вращать, переворачивать, поворачивать или сдвигать. Треугольники совпадают друг с другом и могут быть наложены друг на друга, если их переставить. 3
«Символ конгруэнтности равен ≅. Два треугольника равны, если три стороны и три угла одного треугольника имеют те же размеры, что и три стороны и три угла другого треугольника». 4
Конгруэнтные треугольникиПрименение конгруэнтности треугольников в реальном мире
Инженерное дело и архитектура
Конгруэнтные треугольники используются в процессе строительства для укрепления каркаса.
Это гарантирует жесткость и прочность конструкций. В результате на них не влияют сильные ветры или другие погодные условия. Без них невозможно построить большие искусственные сооружения. Учитывая, что треугольник является одной из самых стабильных форм, а конгруэнтность необходима для создания ровных поверхностей, это так. В геометрическом искусстве, рисунках ковров, узорах ступеней и архитектурных проектах также часто используются конгруэнтные треугольники.
Двумя наиболее распространенными примерами могут быть:
- Ферменный мост: Равносторонние треугольники используются для создания ферменных мостов с обеих сторон. Все эти треугольники соответствуют критерию конгруэнтности SSS, который гласит, что если длина трех сторон одного треугольника равна длине трех сторон другого треугольника, то говорят, что два треугольника конгруэнтны. Это связано с тем, что ферменный мост требует одинаковой длины для контроля веса, чтобы поддерживать конструкцию и предотвращать обрушение. 3
3 - Геодезический купол: это обычное игровое оборудование. Углы и длины сторон должны быть созданы такими, чтобы все задействованные треугольники были конгруэнтны по правилу SAS. Правило SAS гласит, что если две стороны треугольника и угол между ними равны двум сторонам и углу другого треугольника, то эти два треугольника конгруэнтны. Если не быть осторожным, одна ошибка с точки зрения угла, длины стороны или конгруэнтности может быть настолько опасной, что может стать фатальной. 3
Легенда
Знаете ли вы, что существует известная легенда, связанная с использованием конгруэнтных треугольников? Легенда гласит, что один из офицеров Наполеона вычислил ширину реки с помощью равных треугольников. Офицер опускал козырек фуражки до тех пор, пока край противоположного берега не стал самой дальней вещью в поле его зрения, когда он стоял прямо на берегу реки. После этого он повернулся и отметил место на своей стороне реки, которое было параллельно его глазу и кончику визора.
Конгруэнтность — интригующая идея, которая помогает нам развивать и укреплять наши способности к математическому мышлению. Время от времени он может служить мерилом совершенства и быть важным компонентом обеспечения качества. Путь к пониманию сложных концепций геометрии становится немного легче после достижения этой вехи в изучении формы. 1 После прочтения приведенных выше примеров, если вы чувствуете вдохновение искать конгруэнтность в своем окружении, сделайте это. Вы также можете прочитать о более интересных формах, таких как радиальные формы в природе и симметрия в пространстве. Вы также можете посетить блог BYJU’s FutureSchool, чтобы прочитать больше таких увлекательных статей.
Ссылки:
- 20 реальных примеров конгруэнтных чисел – числовая дислексия . (н.д.). Получено 5 июля 2022 г. с https://numberdyslexia.com/real-life-examples-of-congruent-figures/
- Конгруэнтные треугольники — объяснение и примеры . (н.д.). Получено 5 июля 2022 г. с https://www.storyofmathematics.com/congruent-triangles/
- 3 лучших применения конгруэнтных треугольников в реальной жизни . (н.д.). Получено 5 июля 2022 г. с https://icrowdnewswire.com/2021/06/14/top-3-real-life-applications-of-congruent-triangles/ 9.0066
- Конгруэнтные треугольники . (н.д.). Получено 5 июля 2022 г. с https://www.cliffsnotes.com/study-guides/geometry/triangles/congruent-triangles
- Приложения в реальном мире — Понимание конгруэнтности и сходства с использованием физических моделей . (н.д.). Получено 5 июля 2022 г. с https://understandingcongruences.weebly.com/real-world-applications.html
(н.д.). Получено 5 июля 2022 г. с https://numberdyslexia.com/real-life-examples-of-congruent-figures/Математика, Мир математики
Вам также может понравиться
Как создать мобильную математическую игру? Нет сомнений в том, что мобильные устройства повсюду, и с появлением мощных смартфонов и планшетов не видно конца Подробнее.
..Конгруэнтность
Два равных угла , если оба имеют одинаковую меру. На диаграмме конгруэнтные углы обычно обозначаются одинаковым количеством угловых маркеров. Символ≅используется для алгебраического выражения равенства двух углов. Два равных сегмента , если оба имеют одинаковую длину. На диаграмме конгруэнтные сегменты обычно обозначаются одинаковым количеством делений. Символ
≅используется для алгебраического выражения конгруэнтности двух сегментов. Следовательно, если AB=CD, то AB≅CD. Две фигуры являются конгруэнтными фигурами , если существует ор твердых движений, отображающий одну из фигур на другую. В результате конгруэнтные фигуры имеют одинаковый размер и форму. Чтобы алгебраически обозначить, что две фигуры конгруэнтны, символ
≅используется. При написании конгруэнтности соответствующие должны быть перечислены в том же порядке. Для приведенных выше многоугольников два возможных утверждения о конгруэнтности можно записать следующим образом.
ABCDE≅JKLMNorCDEAB≅LMNJK
Два конгруэнтны тогда и только тогда, когда их стороны и углы конгруэнтны.
Используя показанные треугольники, это утверждение можно записать алгебраически следующим образом.
△ABC≅△DEF⇕AB≅DEBC≅EFAC≅DFи∠A≅∠D∠B≅∠E∠C≅∠F
Это доказательство будет построено на основе данной схемы, но справедливо для любой пары треугольников. Доказательство этого состоит из двух частей, по одной для каждого направления.
- Если △ABC и △DEF равны, то их соответствующие стороны и углы равны.
- Если соответствующие стороны и углы △ABC и △DEF равны, то треугольники равны.
Часть 1
По определению конгруэнтных фигур, если треугольники конгруэнтны, существует или, которое отображает △ABC на △DEF. Поскольку твердые движения сохраняют длины сторон, AB и его имеют одинаковую длину, то есть AB=DE. Следовательно, АВ≅DE. Аналогично для двух других длин сторон.BC≅EF и AC≅DF
Кроме того, жесткие движения сохраняют меры.
Тогда ∠A и его образ имеют одинаковую меру, то есть m∠A=m∠D. Следовательно, ∠A≅∠D. Аналогично для остальных углов.∠B≅∠Eand∠C≅∠F
Таким образом, было показано, что если два треугольника конгруэнтны, то их соответствующие стороны и углы конгруэнтны.Часть 2
Для начала отметьте конгруэнтные части на данной диаграмме.
Основная цель — найти жесткое движение или последовательность жестких движений, которые отображают один треугольник в другой. Это можно сделать несколькими способами, здесь показан один из них.
Применить a к △ABC, который отображает A в D. Если этот перевод отображает △ABC на △DEF, доказательство будет завершено. Как видно, △A′B′C′ не соответствует △DEF. Следовательно, необходимо второе жесткое движение. Применить по часовой стрелке к △DB’C’ от D до ∠EDB’. Если изображение соответствует △DEF, доказательство будет завершено. Обратите внимание, что это вращение отображает B’ на E и, следовательно, DB’ на DE. Как и прежде, изображение не соответствовало △DEF.
Таким образом, требуется третье жесткое движение. Подайте заявку в △DEC» через DE . Поскольку отражения сохраняют углы, DC» отображается на DF , а EC» отображается на EF . Затем пересечение исходных лучей C′′ сопоставляется с пересечением лучей изображения F. На этот раз изображение соответствовало △DEF.Следовательно, путем применения различных жестких движений, △ABC было отображено на △DEF. Это означает, что △ABC и △DEF конгруэнтны. Тогда доказательство завершено.
Две стороны конгруэнтны и конгруэнтны.
Используя показанные многоугольники, это утверждение можно записать алгебраически следующим образом.
ABCD≅PQRS⇕ABBCCDAD≅PQ≅QR≅RS≅PSand∠A≅∠B≅∠C≅∠D≅∠P∠Q∠R∠S
Это доказательство будет разработано на основе данной диаграммы, но справедливо для любой пары многоугольников. Доказательство этого состоит из двух частей, по одной для каждого направления.
- Если ABCD и PQRS равны, то их соответствующие стороны и углы равны.
- Если соответствующие стороны и углы ABCD и PQRS равны, то многоугольники равны.
Часть 1
Согласно определению конгруэнтных фигур, если многоугольники конгруэнтны, существует или , которое отображает ABCD на PQRS.
Поскольку твердые движения сохраняют длины сторон, AB и его имеют одинаковую длину, то есть AB=PQ. Следовательно, отрезки AB и PQ конгруэнтны. Аналогичные наблюдения справедливы и для остальных трех сторон.BC≅QRCD≅RSAD≅PS
Кроме того, жесткие движения сохраняют меры, а это означает, что ∠A и ее образ имеют одинаковую меру. Поскольку m∠A=m∠P, углы ∠A и ∠P равны. Точно так же можно сделать вывод, что все остальные углы равны.∠B≅∠Q∠C≅∠R∠D≅∠S
Таким образом было показано, что если два многоугольника конгруэнтны, то их соответствующие стороны и углы конгруэнтны.Часть 2
Для начала на данной диаграмме будут отмечены конгруэнтные части.
Основная цель этой части — найти жесткое движение или последовательность жестких движений, которые отображают один полигон на другой.
Это можно сделать несколькими способами, и здесь показан только один из них. Примените a, отображающий D на S. Если этот перевод отображает ABCD на PQRS, доказательство будет завершено. Как видно, A’B’C’D’ не отображается на PQRS. Следовательно, необходимо второе жесткое движение. Применить по часовой стрелке вокруг S через ∠RSC’ до A’B’C’S. Если изображение соответствует PQRS, доказательство будет завершено. Обратите внимание, что это вращение отображает C ‘на R и, следовательно, SC’ на SR. Изображение по-прежнему не соответствует PQRS, поэтому требуется третье жесткое движение. Наконец, примените а через RS к A»B»RS. Поскольку отражения сохраняют углы и длины, SA» отображается на SP, а RB» отображается на RQ. Точно так же A′′B′′ отображается на PQ. На этот раз изображение соответствует PQRS. Следовательно, путем применения ряда различных жестких движений ABCD был отображен на PQRS. Это означает, что многоугольники ABCD и PQRS конгруэнтны.