Контрольная работа по теме «Множества и операции над ними»
Контрольная работа по теме«Множества и операции над ними»
На каком рисунке изображены отношения между множествами, если:
С – множество двузначных чисел,
D ={3, 34, 43, 56, 103}?
а) б) в) г)
2. На каком рисунке изображены отношения между множествами, если:
С – множество двузначных чисел,
D – множество натуральных чисел, не меньших 10?
а) б) в) г)
3. Какое высказывание является верным, если:
А – множество натуральных чисел, кратных 2
В – множество натуральных чисел, кратных 6?
а) А б) В в) А В г) А = В
Пересечение множеств решений неравенств х и х изображено на рисунке
а)
б)
в)
г)
д)
Объединение множеств решений неравенств х и х изображено на рисунке
а)
б)
в)
г)
д)
6.
Объединение множеств решения неравенств х — 5 и х ≤ 7, 5 изображено на рисунке
а)
б)
в)
г)
д)
7. Пересечение множеств решения неравенств х — 5 и х ≤ 7, 5 изображено на рисунке
а)
б)
в)
г)
д)
8. Какая фигура принадлежит пересечению множеств С и D, если:
С – множество ромбов;
D – множество прямоугольником.
а) ромб
б) прямоугольник
в) квадрат
9. Какие треугольники не принадлежит объединению множеств, если:
С – множество равнобедренных треугольников;
D–множество прямоугольных треугольников?
а) прямоугольные равнобедренные;
б) равнобедренные, но не прямоугольные;
в) прямоугольные, но не равнобедренные;
г) не прямоугольные и не равнобедренные.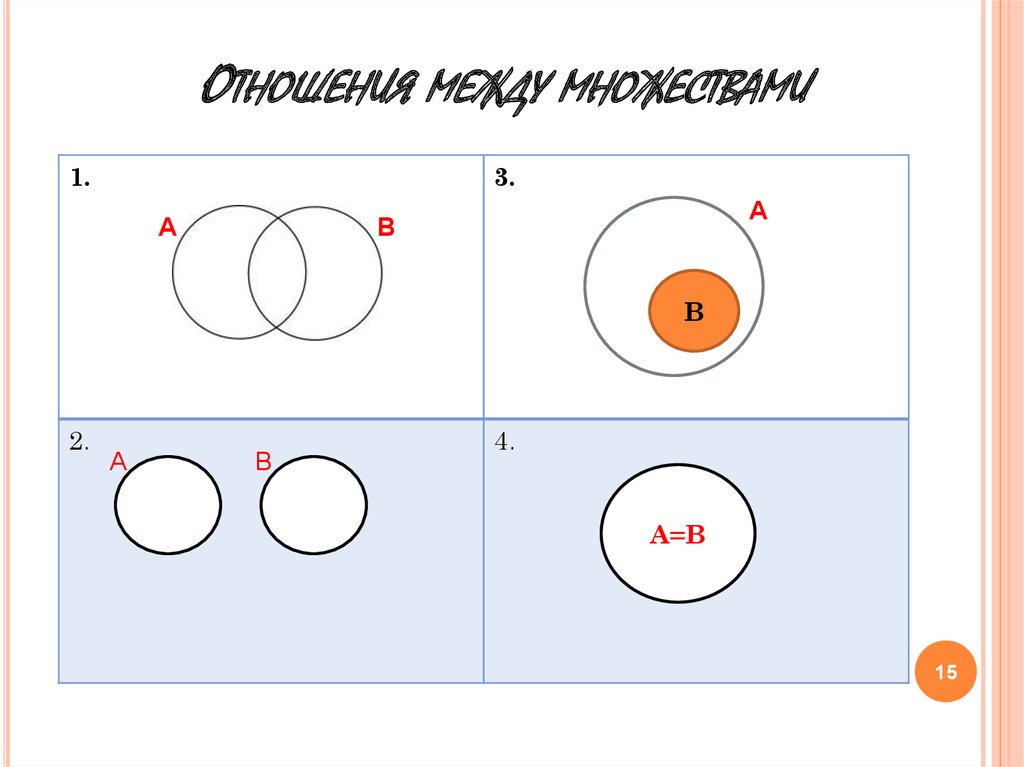
Множеству Р равно множество:
а) Р б) (М в) (Р
11. А – множество натуральных чисел кратных 4, С – множество натуральных чисел кратных 2. Множеству С \ А принадлежит
а) 8 б) 12 в) 26 г) 13
12. Реши задачу
Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной. 8 человек занимается и в той, и в другой секции. Сколько школьников не занимается ни в баскетбольной, ни в волейбольной секции?
а) 3 б) 13 в) 19
13. При помощи отношения « иметь один и тот же остаток при делении на 3» множество натуральных чисел разбивается на
а) два класса; б) три класса; в) четыре класса.
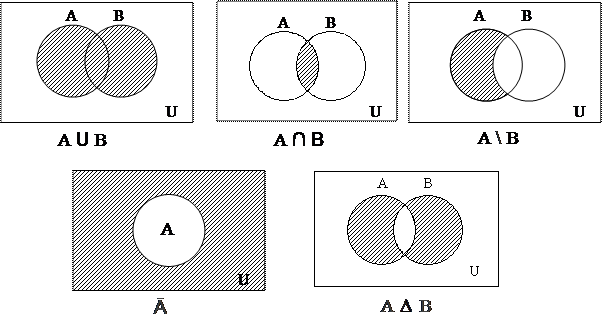
14. Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству
а) А и множеству В;
б) А или множеству В;
в) А, но не принадлежат множеству В;
г) В, но не принадлежат множеству А;
15.
Пересечением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству
а) А и множеству В;
б) А или множеству В;
в) А, но не принадлежат множеству В;
г) В, но не принадлежат множеству А;
16.Верным является равенство
а) А Ø = Ø
б) А Ø = Ø
в) А Ø = А
г) А А = Ø.
Если А В, то
а) А В = А
б) А В = В
в) А В = А
г) А В = А В
18.У Коли 10 книг, 2 книги он подарил другу. Сколько книг у него осталось? Над множествами в задаче выполняются операции:
а) Объединение;
б) Пересечение;
в)Разбиение множества на классы;
г) Вычитание множеств.
19.У школы посадили 4 липы и 3 березы. Сколько всего деревьев посадили у школы? Над множествами в задаче выполняются операции:
а) Объединение;
б) Пересечение;
в)Разбиение множества на классы;
г) Вычитание множеств.
Запиши по порядку числа от 10 до 19. Подчеркни и прочитай четные числа. Над множествами в задаче выполняются операции:
а) объединение;
б) пересечение;
в) разбиение множества на классы;
г) вычитание множеств.
21. А= {1, 3}; В= {3,5}. Декартово произведение множеств А и В ( А х В) изображено на рисунке:
а) б) в) г)
Установи порядок выполнения действий в следующих выражениях
А ∩ В ∩ С
Установи порядок выполнения действий в следующих выражениях
А ∩ В U С ∩ D
Установи порядок выполнения действий в следующих выражениях
А U В ∩ С U D
Установи порядок выполнения действий в следующих выражениях
А \ В ∩ С
5
Дифференцированная контрольная работа по информатике «Основы теории множеств.
Операции над множествами», ФГОС Дифференцированная контрольная работа по информатике «Основы теории множеств. Операции над множествами», ФГОС
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Учебно-дидактические материалы
▪Контрольные / проверочные работы
Материал опубликовал
2
#10 класс #11 класс #Информатика и ИКТ #ФГОС #Учебно-дидактические материалы #Контрольные / проверочные работы #Учитель-предметник #Студент-практикант #Школьное образование #УМК Л.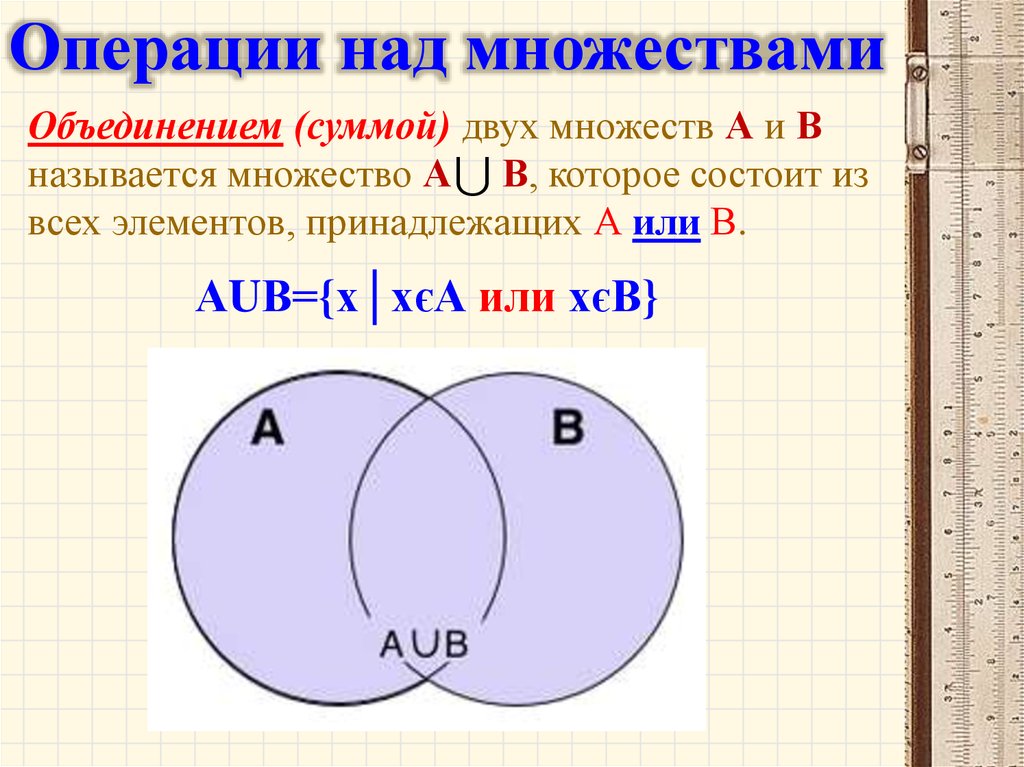
Л. Босовой
Информатика и ИКТ, 10 класс (базовый курс) Контрольная работа по теме «Основы теории множеств» В-1 Задание 1 (базовый уровень): Пусть А=[-5;0), B=(-2;4) – интервальные промежутки целых чисел; С={х|x2+3х-4=0} – множество решений квадратного уравнения. Запишите с помощью перечисления элементов множеств, следующие операции: а) б) в) г) д) Задание 2 (повышенный уровень): Выразите через базовые множества и операции над ними закрашенную область: задача 1: задача 2: Задание 3 (высокий уровень): В таблице приведены операции над множествами и количество элементов, которые образовались в областях этих операций:
Какое количество элементов области Слон Жираф? | Информатика и ИКТ, 10 класс (базовый курс) Контрольная работа по теме «Основы теории множеств» В-2 Задание 1 (базовый уровень): Пусть А=(-5;0), B=[2;6) – интервальные промежутки целых чисел; С={х|x2+3х+2=0} – множество решений квадратного уравнения. Запишите с помощью перечисления элементов множеств, следующие операции: а) б) в) г) д) Задание 2 (повышенный уровень): Выразите через базовые множества и операции над ними закрашенную область: задача 1: задача 2: Задание 3 (высокий уровень): В таблице приведены операции над множествами и количество элементов, которые образовались в областях этих операций:
Какое количество элементов области Сыр Масло? |
Ответы (вариант 1) Задание 1. А=(-5, -4, -3, -2, -1) В=(-1, 0, 1, 2, 3) С=(-4, 1) Решение: а) -1 б) 1 в)-5, -3, -2, -1 г) -5, -3, -2, -1, 1 д) -1, -4, 1 Задание 2. Формула 1: А/(ВС) Формула 2: (A (C/(A B) Задание 3. Ответ: Слон Жираф =29 | Ответы (вариант 2) Задание 1. А=(-4, -3, -2, -1) В=(2, 3, 4, 5) С=(-2, -1) Решение: а) -2, -1 б) пустое множество в)-4, -3, -2, -1 г) -4, -3 д) -2, -1 Формула: ABBC Формула 2: С/(А В) Задание 3. Ответ: Сыр Масло =12 |
СПИСОК источников:
Зайдельман Я.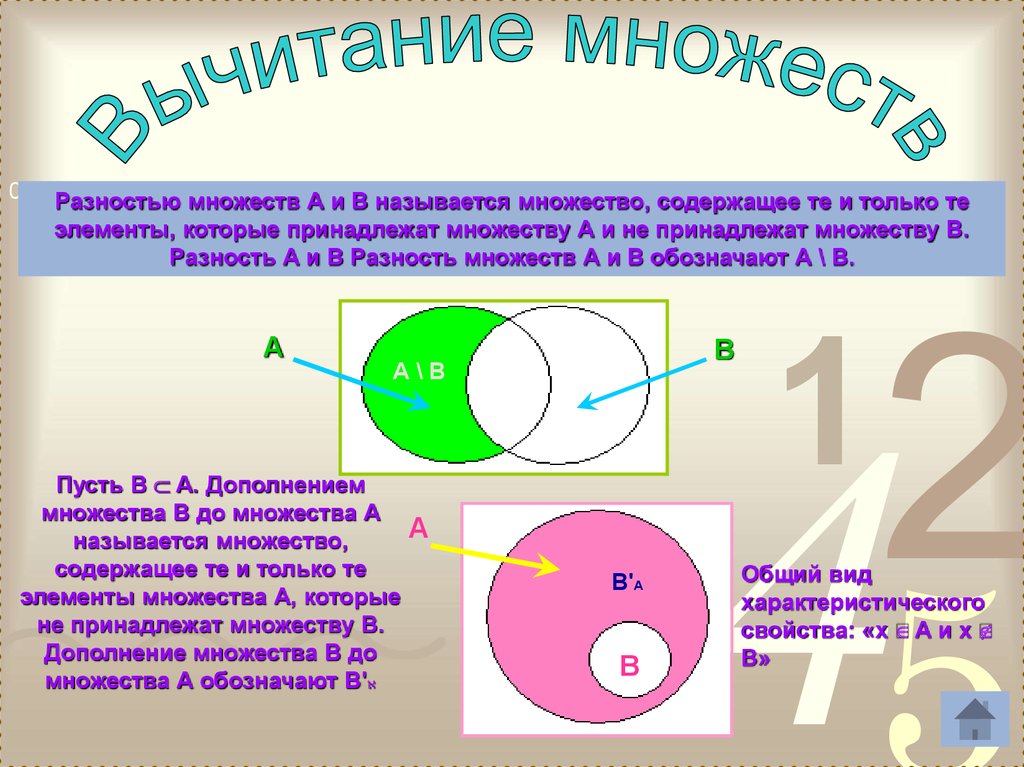
Н., Ройтберг М.А.. Информатика и ИКТ. Подготовка к ЕГЭ в 2019+ году. Диагностические работы. – М.: МЦНМО, 2019 (содержание таблицы задания 2).
Иллюстрации:
http://ok- t.ru/life-prog/baza2/4833562664643.files/image346.jpg
https://ru-static.z-dn.net/files/d8e/be284714eeccae1af00e51be4c0476a1.jpg
https://ds04.infourok.ru/uploads/ex/136b/00030d22-6c4291c6/img24.jpg
https://otvet.imgsmail.ru/download/u_ce1ea3cebf96cb95f76ac06d34a81e3b_800.png
Опубликовано
в группе «УРОКИ, КИМы, ИГРЫ, практикумы, творческие задания по ИНФОРМАТИКЕ, МАТЕМАТИКЕ и другим дисциплинам.»
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
Операции над множествами
Горячая математика Напомним, что
набор
представляет собой набор элементов.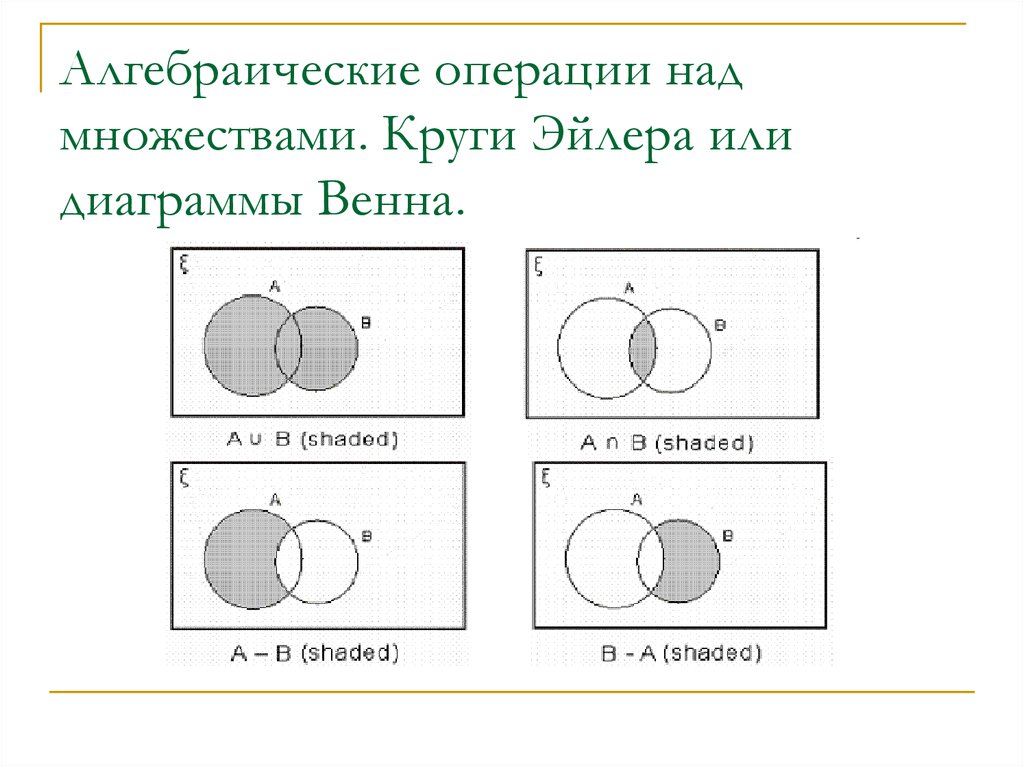
Данные наборы А и Б , мы можем определить следующие операции:
Операция | Обозначение | |
Перекресток | А ∩ Б | все элементы, которые есть в обоих А и Б |
Союз | А ∪ Б | все элементы, которые находятся в любом А или Б (или оба) |
Разница | А − Б | все элементы, находящиеся в А но не в Б |
Дополнение | А ¯ (или А С ) | все элементы, которых нет в А |
Пример 1:
Позволять
А
«=»
{
1
,
2
,
3
,
4
}
и разреши
Б
«=»
{
3
,
4
,
5
,
6
}
.
Затем:
А ∩ Б «=» { 3 , 4 }
А ∪ Б «=» { 1 , 2 , 3 , 4 , 5 , 6 }
А − Б «=» { 1 , 2 }
А С «=» { все действительные числа, кроме 1 , 2 , 3 и 4 }
Пример 2:
Позволять
А
«=»
{
у
,
г
}
и разреши
Б
«=»
{
Икс
,
у
,
г
}
.
Затем:
А ∩ Б «=» { у , г } А ∪ Б «=» { Икс , у , г } А − Б «=» ∅ А С «=» { все, кроме у и г }
Операции над множествами — формулы, свойства, примеры
Операции над множествами — это концепция, аналогичная основным операциям над числами. Множества в математике имеют дело с конечным набором объектов, будь то числа, алфавиты или любые объекты реального мира.
Иногда возникает необходимость установить связь между двумя или более множествами. Возникает понятие операций над множествами.
Существует четыре основных операции над множествами, включая объединение множеств, пересечение множеств, дополнение множеств и разность множеств. В этой статье мы изучим различные операции с множествами, обозначения представления множеств, способы работы с множествами и их использование в реальной жизни.
| 1. | Что такое операции над множествами? |
| 2. | Базовый набор операций |
| 3. | Свойства операций над множествами |
| 4. | Часто задаваемые вопросы по работе с наборами |
Что такое операции над множествами?
Набор определяется как набор объектов. Каждый объект внутри набора называется «Элемент». Множество может быть представлено в трех формах.
Это форма заявления, форма списка и нотация построителя наборов. Операции над множествами — это операции, которые применяются к двум или более множествам для установления связи между ними. Существует четыре основных типа операций над множествами, которые заключаются в следующем.
- Набор комплектов
- Пересечение наборов
- Дополнение к набору
- Разница между комплектами/относительное дополнение
Прежде чем мы перейдем к обсуждению различных операций над множествами, давайте вспомним концепцию диаграмм Венна, поскольку она важна для понимания операций над множествами. Диаграмма Венна — это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Диаграмму Венна можно представить следующим образом.
Базовый набор операций
Теперь, когда мы знаем концепцию множества и диаграммы Венна, давайте подробно обсудим каждую операцию над множеством. Различные операции над множествами:
Объединение множеств
Для двух заданных множеств A и B, A∪B (читается как объединение B) — это множество различных элементов, которые принадлежат множеству A и множеству B или обоим.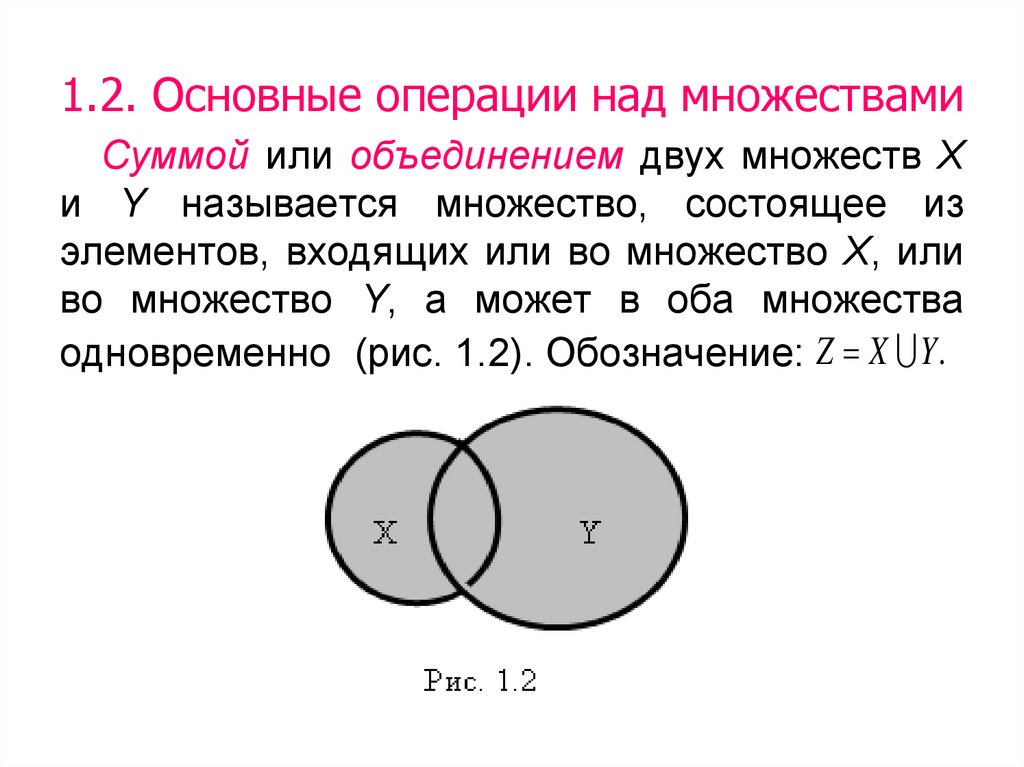
Количество элементов в A ∪ B определяется выражением n(A∪B) = n(A) + n(B) − n(A∩B), где n(X) — количество элементов в множестве X. Чтобы Чтобы лучше понять эту операцию объединения множеств, давайте рассмотрим пример: если A = {1, 2, 3, 4} и B = {4, 5, 6, 7}, то объединение A и B равно определяется как A ∪ B = {1, 2, 3, 4, 5, 6, 7}.
Пересечение множеств
Для двух заданных множеств A и B, A ∩ B (читается как пересечение A B) — это множество общих элементов, принадлежащих множествам A и B. Количество элементов в A ∩ B определяется выражением n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы лучше понять эту операцию пересечения множеств, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4} .
Установить разницу
Операция над множествами разница между множествами подразумевает вычитание элементов из множества, что аналогично понятию разности между числами. Разница между наборами A и набором B, обозначенная как A − B, перечисляет все элементы, которые находятся в наборе A, но не в наборе B.
Чтобы лучше понять эту операцию над набором разности наборов, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то разница между множествами A и B определяется соотношением A — B = {1, 2}.
Дополнение к наборам
Дополнение множества A, обозначаемое как A′ или A c (читается как дополнение A), определяется как множество всех элементов данного универсального множества (U), которые не присутствуют в множестве A. Чтобы понять эту операцию дополнения множеств лучше, рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4}, тогда дополнение множества A задается как A’ = {5, 6, 7, 8, 9}.
На изображении выше показаны различные операции над наборами с помощью диаграмм Венна. Когда элементы одного множества B полностью лежат в другом множестве A, то B называется собственным подмножеством A. Когда два множества не имеют общих элементов, они называются непересекающимися множествами. Теперь давайте рассмотрим свойства операций над множествами.
Свойства операций над множествами
Свойства операций над множествами аналогичны свойствам основных операций над числами. Важные свойства операций над множествами указаны ниже:
- Закон перестановочности . Для любых двух заданных множеств A и B свойство перестановочности определяется как
A ∪ B = B ∪ A
Это означает, что множественная операция объединения двух множеств коммутативна.
А ∩ В = В ∩ А
Это означает, что множественная операция пересечения двух множеств коммутативна. - Ассоциативный закон — Для любых трех заданных наборов A, B и C свойство ассоциативности определяется как
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Это означает, что операция объединения множеств ассоциативна.
(А ∩ В) ∩ С = А ∩ (В ∩ С)
Это означает, что операция пересечения множеств ассоциативна. - Закон Де-Моргана — Закон Де Моргана гласит, что для любых двух множеств A и B мы имеем (A ∪ B)’ = A’ ∩ B’ и (A ∩ B)’ = A’ ∪ B’
- А ∪ А = А
- А ∩ А = А
- А ∩ ∅ = ∅
- А ∪ ∅ = А
- А ∩ В ⊆ А
- А ⊆ А ∪ В
Важные замечания по операциям над множествами
- Формула операции над множествами для объединения множеств: n(A∪B) = n(A) + n(B) − n(A∩B) и формула операции над множествами множества есть n(A∩B) = n(A)+n(B)−n(A∪B).
- Объединение любого множества с универсальным множеством дает универсальное множество, а пересечение любого множества А с универсальным множеством дает множество А.
- Объединение, пересечение, разность и дополнение — это различные операции над множествами.
- Дополнением универсального множества является пустое множество U′ = ϕ. Дополнением пустого множества является универсальное множество ϕ′ = U.
Связанные темы по операциям над множествами
- Надмножество
- Силовой набор
- Конечные и бесконечные наборы
Часто задаваемые вопросы по работе с наборами
Что такое
Операции над множествами в теории множеств?Операции над множествами — это операции, применяемые к двум или более множествам для установления связи между ними. Существует четыре основных вида операций над множествами.
Каковы различные операции над наборами?
Существует четыре основных вида операций с наборами:
- Набор комплектов
- Пересечение наборов
- Дополнение к набору
- Разница между комплектами/относительное дополнение
Как мы используем операции над множествами в реальной жизни?
Набор — это набор элементов.
Некоторые примеры наборов из реальной жизни — это список всех штатов в стране, список всех фигур в геометрии, список всех целых чисел от 1 до 100. Мы можем определить общие области, используя операцию пересечения множества.
Как вы решаете проблемы с работой набора?
Для решения задач с операциями над множествами мы используем диаграмму Венна для представления отношений между множествами и применяем формулу операций над множествами для объединения, пересечения, разности или дополнения множества.
Какие из операций над множествами являются коммутативными и некоммутативными?
Объединение и пересечение множеств являются коммутативными операциями над множествами, в то время как разность множеств не является коммутативной.
Что такое набор символов операций?
Существуют различные символы, используемые для различных операций над множествами, которые называются обозначениями множеств. Для объединения множеств мы используем ‘ ∪ ‘, для пересечения множеств используем ‘∩’, для разности множеств используем ‘-‘, а для дополнения множества A мы пишем как A’ или A c .