формула, формулировка простыми словами, кто открыл, задачи с решением, примеры из жизни
Энергия — одно из сложнейших понятий современной физики. И закон сохранения энергии относится к числу ее основополагающих принципов. Вместе с экспертом разберем задачи с решением этого фундаментального закона природы и узнаем, кто его открыл
Закон сохранения энергии. Фото: pixabay.comАндрей Найденов Преподаватель математики и физики онлайн-школы TutorOnline Борис Михеев Автор КП
Содержание
- Формулировка закона
- Формула
- История
- Задачи с решениями
- Вопросы и ответы
Физика ставит своей целью понимание самых общих закономерностей материального мира. Имена Архимеда, Ньютона, Эйнштейна знакомы каждому школьнику. Но великое множество ученых вложили по кирпичику в здание современной науки и ускорили развитие человеческой цивилизации. Ее современный уровень был бы недостижим без понимания природы энергии и ее законов прежде всего в механике, самом доступном для наблюдений и экспериментов разделе физики.
Имена Архимеда, Ньютона, Эйнштейна знакомы каждому школьнику. Но великое множество ученых вложили по кирпичику в здание современной науки и ускорили развитие человеческой цивилизации. Ее современный уровень был бы недостижим без понимания природы энергии и ее законов прежде всего в механике, самом доступном для наблюдений и экспериментов разделе физики.
Формулировка закона сохранения энергии простыми словами в механике
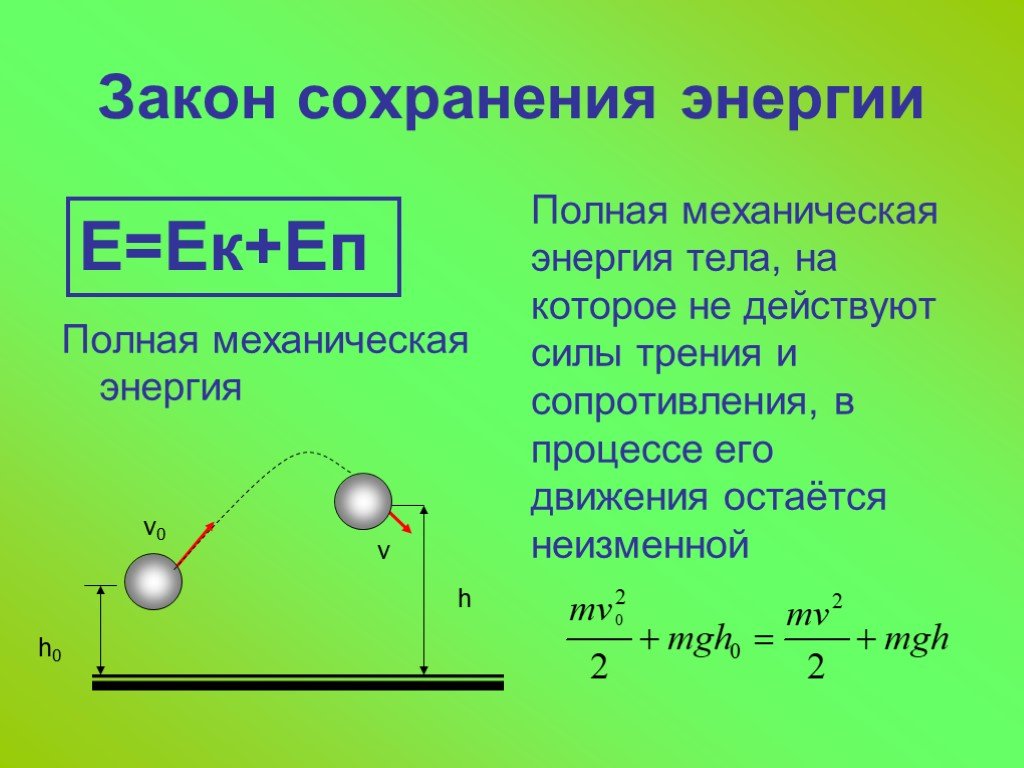
Закон сохранения энергии действует повсеместно и незаметно. В механике он срабатывает в замкнутой системе под воздействием консервативных сил – то есть сил тяжести и упругости, зависящих только от стартового и финального положения тела и не зависящих от траектории движения. При таких условиях энергия тел никуда не исчезает, а лишь переходит из кинетической в потенциальную и наоборот – из потенциальной в кинетическую. Это и есть самая простая формулировка закона сохранения энергии для механических систем.
Формула закона сохранения энергии
E=Ep+Ek=const
Где:
Ep — потенциальная энергия;
Ek — кинетическая энергия;
 Фото pixabay.com
Фото pixabay.comИстория открытия закона сохранения энергии
Закономерности взаимодействия физических тел интересовали ученых с античных времен. Но описать их в виде формулы или хотя бы принципа они не сумели. Первым это попытался сделать Рене Декарт в своем труде «Начала философии», изданном в середине XVII века. Он указал, что если одно тело сталкивается с другим, то может отдать ему только такое количество движения, сколько второе у него отнимет. Идею Декарта развил Лейбниц, введя понятие «живой силы», которую мы называем кинетической энергией. Поддержал его рассуждения Михайло Ломоносов в своем «всеобщем естественном законе», но все формулировки были скорее принципом, а не законом, формул не было.
От «живой силы» физики перешли к «кинетической энергии» только в середине XIX столетия, накопив опыт работы с тепловыми и электрическими машинами. Немалый экспериментальный вклад сделал в понимание этого закона Джеймс Джоуль и Роберт Майер. Самую полную математическую формулировку дал Герман Гельмгольц, который ввел понятие потенциальной энергии и обобщил закон сохранения энергии на все разделы физики – даже на те, которые в его время не существовали.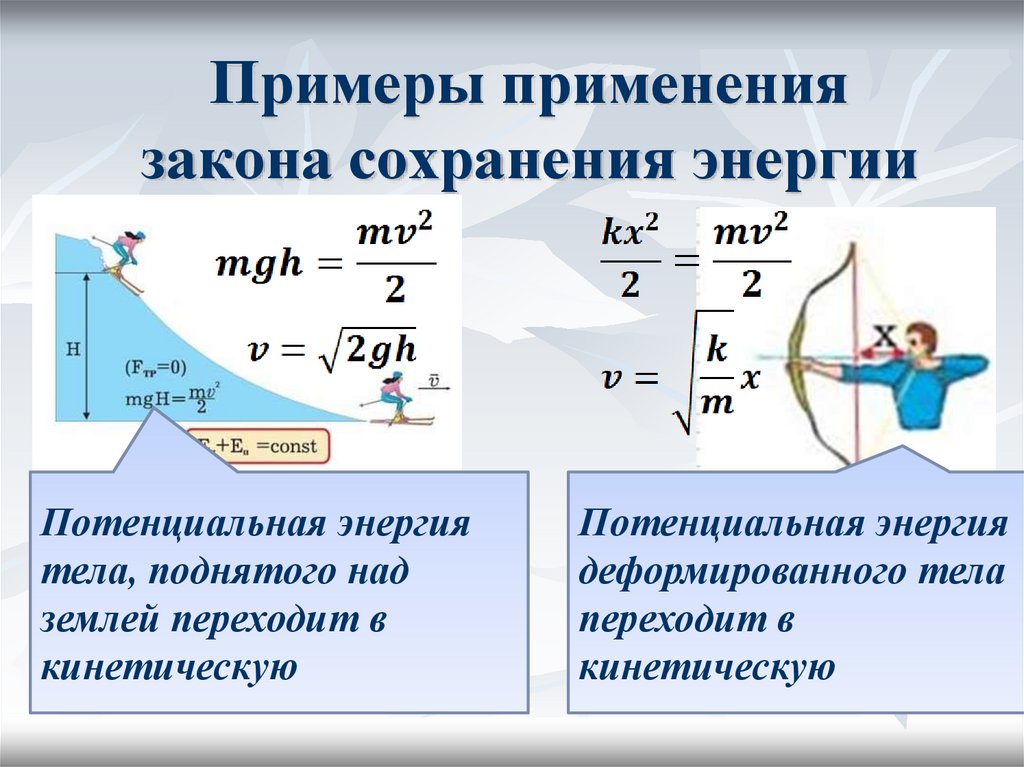 Например, на теорию относительности и квантовую механику.
Например, на теорию относительности и квантовую механику.
Задачи на закон сохранения энергии
Самый общий физический закон используется при решении совершенно практических задач.
Задача 1
Некое тело подбросили вверх вертикально с начальной скоростью 15 м/с. На какую высоту оно поднимется? Сопротивление воздуха при решении задачи не учитывать.
Решение: полученная при броске кинетическая энергия будет постепенно преобразовываться в потенциальную энергию:
Ep=Ek
То есть: mgh=(m*V2)/2
Где:
m – масса тела;
V – начальная скорость;
g – ускорение свободного падения;
h – высота подъема.
После преобразований получаем формулу для высоты подъема:
h= V2/(2*g)=225/(2*9,8)=11,47 м.
Ответ: тело поднимется на высоту 11,47 м.
это интересно
Сила Архимеда
Формула и определение силы Архимеда простыми словами
подробнее
Задача 2
Пружину растянули на 15 см. Известно, что она получила потенциальную энергию 24 Дж. Какова жесткость пружины?
Известно, что она получила потенциальную энергию 24 Дж. Какова жесткость пружины?
Решение: формула потенциальной энергии упруго деформированного тела:
Ep=(k*x2)/2
Где:
k – коэффициент жесткости;
x – величина деформации.
Преобразуем формулу для расчета:
k=(2*Ep)/x2=(2*24)/225=2133,33 Н/м
Ответ: жесткость пружины равна 2133,33 Н/м.
Популярные вопросы и ответы
Отвечает Андрей Найденов, преподаватель математики и физики онлайн-школы TutorOnline.
Кто открыл закон сохранения энергии?
В открытии закона сохранения энергии участвовали многие ученые. Некоторые из них были очень близки, чтобы сформулировать его. Например, Майер и Джоуль своими работами показали, что количество выделяемой теплоты равно совершенной работе и наоборот. Однако наиболее полную формулировку первым дал в своих работах Гельмгольц.
Какие примеры из жизни на закон сохранения энергии существуют?
Таких примеров множество.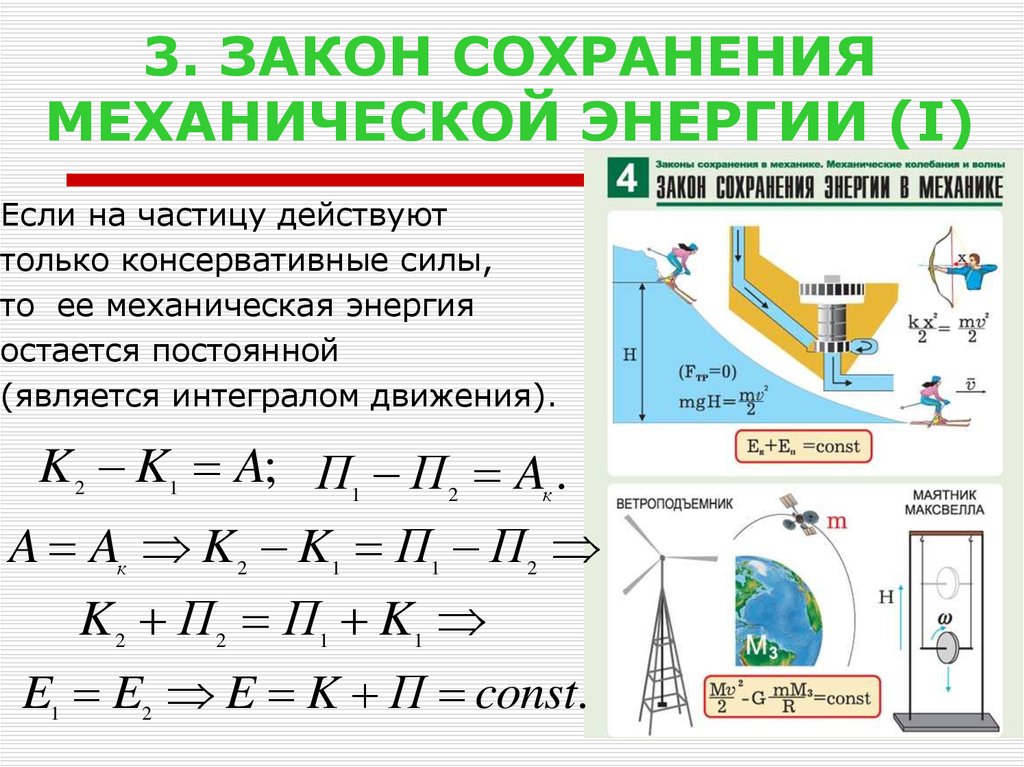 Пример с молотком и гвоздем хорошо иллюстрирует переход механической энергии от молотка к гвоздю. Закон сохранения энергии здесь в том, что сколько молоток при ударе энергии отдал, столько же энергии гвоздь и получил. Ни больше ни меньше.
Пример с молотком и гвоздем хорошо иллюстрирует переход механической энергии от молотка к гвоздю. Закон сохранения энергии здесь в том, что сколько молоток при ударе энергии отдал, столько же энергии гвоздь и получил. Ни больше ни меньше.
Другой пример. Кубики льда, взятые при температуре 0º С и опущенные в бокал с газированной водой, растаят, если им сообщить столько же Джоулей тепла, сколько забрали тепла у воды, взятой при температуре 0º С, когда ее замораживали, чтобы она перешла в твердое агрегатное состояние – лед. А если газированная вода будет недостаточно теплой, то лед не растает. Однако если этот бокал оставить на столе надолго, лед все равно растает, так как он получит необходимое количество тепла из окружающего воздуха.
Еще пример. Когда болит горло, есть хороший бабушкин рецепт. Надо пить теплое молоко. Молоко прогревает горло, отдает тепло, что помогает лечению. Молоко при этом остывает в горле и не греет желудок, что тоже важно.
Во всех этих примерах можно наблюдать большие потери тепла на нагрев окружающих тел.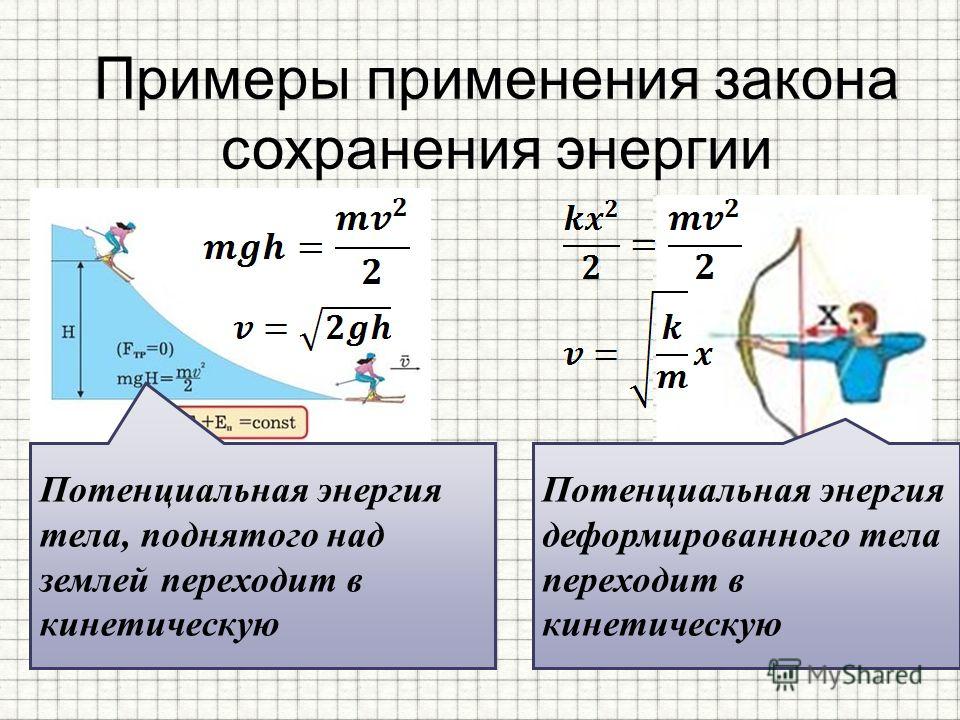 Но основная часть энергии идет на полезное действие. Сколько энергии отдает одно тело, столько же получает и другое, минус потери тепла на нагрев окружающих тел.
Но основная часть энергии идет на полезное действие. Сколько энергии отдает одно тело, столько же получает и другое, минус потери тепла на нагрев окружающих тел.
Если исключить потери тепла, можно добиться очень высокой эффективности процесса. Это возможно в системах, где энергия не выходит наружу и не рассеивается, поэтому ее потери минимальные. Примером такой системы может служить термос. Горячая вода в термосе долго не остывает, потому что потери тепла минимальные.
Когда сохраняется полная механическая энергия?
Полная механическая энергия сохраняется в системах, которые называются изолированными. Получить полностью изолированную систему достаточно сложно. Всегда найдутся силы, которые будут действовать на тело или систему из нескольких тел извне.
Хорошим примером может стать жизнь космонавтов на орбитальном комплексе, вращающемся вокруг Земли. Если космонавт оттолкнется от пола на Земле, то сила притяжения быстро вернет его обратно на пол.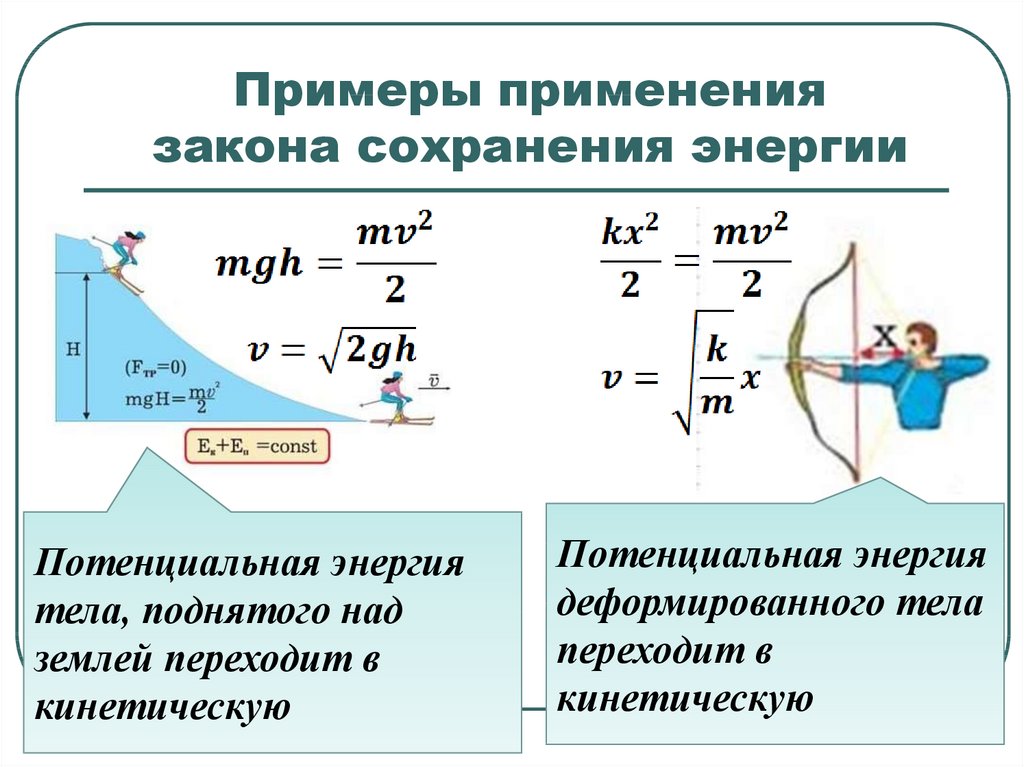
В орбитальном комплексе сила притяжения к Земле скомпенсирована движением корабля по круговой орбите. Состояние невесомости позволяет космонавту оттолкнутся от пола и лететь вверх неопределенно долго, пока он не столкнется с потолком. Тело космонавта можно считать изолированной системой, так как на него не действуют силы извне, а силы сопротивления движению со стороны воздуха в корабле минимальны.
В каком классе изучают закон сохранения энергии?
Здесь есть одна тонкость. Закон сохранения механической энергии изучают на уроках физики в седьмом классе. А закон сохранения энергии, применительно к тепловым процессам, с использованием понятия внутренней энергии тела, изучают уже в восьмом классе.
когда его придумали в физике, история
Закон сохранения энергии считается фундаментальной научной теорией, которая была установлена эмпирическим способом. Она оказала значительное влияние на последующее развитие физики и прочих научных отраслей. При этом далеко не каждому человеку известно, кто конкретно открыл закон сохранения энергии. На самом деле вклад в появление этой теории внес далеко не один ученый.
На самом деле вклад в появление этой теории внес далеко не один ученый.
Содержание
Описание закона
Эта теория представляет собой фундаментальный закон природы, который был установлен эмпирическим способом. Он заключался в том, что для изолированной физической системы можно ввести скалярный физический параметр. Он представляет собой функцию показателей системы и называется энергией, которая способна с течением времени сохраняться. Так как этот закон нельзя отнести к конкретным параметрам и явлениям, и он в большей степени отражает общую закономерность, данное понятие можно называть принципом сохранения энергии.
Фундаментальная суть этот понятия раскрывается в теореме Нетер. Согласно ей, любой закон сохранения четко соответствует определенной системе уравнений, которые описывают физическую систему. Так, закон сохранения энергии стоит считать эквивалентным однородности времени. Это означает, что все законы, описывающие систему, не зависят от момента времени, в котором она рассматривается.
Под влиянием исторических факторов этот закон в разных разделах физики имел независимые формулировки. Именно поэтому стали применять разные виды энергии. Существует мнение, что один тип энергии может переходить в другой. Однако полная энергия системы, которая равна сумме отдельных видов, остается неизменной. Поскольку деление этого понятия на разновидности носит весьма условный характер, его нельзя провести однозначно.
Для каждого из видов энергии закон сохранения может отличаться своей формулировкой, которая имеет некоторые отличия от универсальной. К примеру, в классической механике применяется закон механической энергии, электродинамика использует теорему Пойнтинга, а термодинамика – первое начало термодинамики. При этом важно знать, кто придумал эту теорию.
При этом важно знать, кто придумал эту теорию.
Формулы и единицы измерения
Полная механическая энергия представляет собой сумму кинетической и потенциальной энергии тела. Потому формула закона сохранения энергии выглядит так:
E=Ep+Ek=const,
где Ep – потенциальная энергия;
Ek – кинетическая энергия.
Эта величина измеряется в джоулях. Важно учитывать, что оба вида энергии могут меняться. К примеру, во время падения мяча показатели кинетической энергии увеличиваются, поскольку скорость движения нарастает. При этом потенциальные параметры уменьшаются, так как сокращается высота тела по отношению к земле. Это позволяет понять, какие разные виды энергии переходят друг в друга. При этом полный параметр остается постоянным при условии отсутствия сопротивления воздуха и других энергетических потерь.
Примеры закона в реальной жизни
Превращение одного вида энергии в другой можно понять с помощью простых бытовых примеров. Одним из них может стать забивание гвоздя с помощью молотка. Этот процесс наглядно демонстрирует передачу механической энергии от молотка к гвоздю. Закон в данном случае заключается в том, что, сколько молоток отдает энергии при ударе, ровно столько же получает гвоздь.
Этот процесс наглядно демонстрирует передачу механической энергии от молотка к гвоздю. Закон в данном случае заключается в том, что, сколько молоток отдает энергии при ударе, ровно столько же получает гвоздь.
В качестве другого примера стоит привести кубики льда, погруженные в бокал с газированной водой. Лед растает, если сообщить ему столько же джоулей тепла, сколько забрали у воды при температуре 0 градусов во время заморозки. Если вода окажется недостаточно теплой, лед таять сразу не начнет. Если же бокал оставить на длительное время на столе, кубики все равно растают, так как они получат нужное количество тепла из воздуха.
Также можно привести пример с теплым молоком, которое используют при простуде. Такой напиток прекрасно прогревает горло, отдавая тепло, что помогает вылечиться. При этом молоко остывает в горле и не греет желудок.
Теряется ли энергия при передаче
В указанных примерах наблюдаются значительные теплопотери, которые требуются для нагревания окружающих объектов. Однако большая часть энергетического потенциала расходуется на полезные действия. Если исключить потери тепла, удастся сделать процесс значительно эффективнее. Это возможно в системах, в которых энергия не выходит наружу и не тратится. Потому ее потери являются минимальным. В качестве примера такой системы стоит привести термос. Горячая вода в нем длительное время не остывает, так как теплопотери минимальны.
Однако большая часть энергетического потенциала расходуется на полезные действия. Если исключить потери тепла, удастся сделать процесс значительно эффективнее. Это возможно в системах, в которых энергия не выходит наружу и не тратится. Потому ее потери являются минимальным. В качестве примера такой системы стоит привести термос. Горячая вода в нем длительное время не остывает, так как теплопотери минимальны.
При этом, с точки зрения физики, полная механическая энергия сохраняется в системах, которые называются изолированными. Получить их довольно сложно. Всегда встречаются силы, которые будут действовать извне. В качестве наглядного примера такой системы стоит привести жизнь космонавтов на орбитальном комплексе, который вращается вокруг земли.
Если космонавт оттолкнется от пола на Земле, под влиянием силы притяжения он тут же вернется обратно. В орбитальном комплексе гравитацию компенсирует движение корабля по круговой орбите. В таком случае космонавт находится в состоянии невесомости. Он может оттолкнуться от пола и лететь вверх довольно долго, пока не достигнет потолка.
Он может оттолкнуться от пола и лететь вверх довольно долго, пока не достигнет потолка.
Тело космонавта стоит рассматривать как изолированную систему, поскольку на него не действуют внешние факторы. При этом силы сопротивления движению со стороны воздуха минимальны.
История открытия
Закономерности взаимодействия физических тел интересовали мыслителей еще во времена античности. Однако они не имели возможности описать их с научной точки зрения. Первым это удалось сделать Рене Декарту в работе «Начала философии», которая появилась в середине семнадцатого века. Ученый отмечал, что при столкновении одного тела с другим оно может отдать ему столько движения, сколько второе у него отнимет.
Теорию Декарта впоследствии развил Лейбниц. Он использовал термин «живая сила». Аналогичные рассуждения вел и Михаил Ломоносов. Однако в тот период все формулировки в большей степени представляли собой принцип, тогда как закон и формулы отсутствовали.
Важный вклад в установление количественной связи между теплотой и работой внес французский ученый Сади Карно. Причем интересные рассуждения исследователя были опубликованы уже после его смерти. Он говорил о том, что тело представляет собой движущую силу. Везде, где уничтожается движущая сила, одновременно появляется теплота. При этом ее количество точно пропорционально количеству исчезнувшей движущей силы.
Следующее важное достижение принадлежит немецкому физику Роберту Майеру. По сути, он первым сформулировал закон сохранения энергии. Это случилось в 1842 году. Ученый установил, что химическая реакция приводит к созданию тепла и работы. Они, в свою очередь, вырабатывают еще больше тепла.
Стоит отметить, что открытие Майера не было оценено по достоинству. Это произошло намного позже, когда Джеймс Джоуль опубликовал свой труд. Во время изучения электрических двигателей ученый установил, что тепло, которое проходит через провод, прямо пропорционально количеству выполненной динамо-машиной работы. Он дал этому открытию название теории калорий. В конечном итоге Майеру и Джоулю удалось установить, что работа превращается в количество тепла в том же численном эквиваленте.
Он дал этому открытию название теории калорий. В конечном итоге Майеру и Джоулю удалось установить, что работа превращается в количество тепла в том же численном эквиваленте.
В каком классе проходят эту тему
Закон сохранения механической энергии проходят на уроках физики в седьмом классе. Если же применять эту теорию к тепловым процессам, то эта тема входит в программу восьмого класса.
Закон сохранения энергии считается важнейшей теорией, которая оказала значительное влияние на развитие физики и других дисциплин. Первым ее сформулировал немецкий физик Роберт Майер. Однако свой вклад в появление этого принципа внесли многие ученые.
| Введение В 1842 году Юлиус Роберт Майер открыл закон сохранения энергии. В самой компактной форме он теперь называется Первым законом термодинамики: Энергия не создается и не уничтожается. В начале 20-го века Альберт Эйнштейн объявил об открытии уравнения E= mc2, и, как следствие, два вышеуказанных закона были объединены в Закон сохранения массы-энергии: Общее количество массы и энергии в вселенная постоянна. Что это значит для нас? Ну, эти законы позволяют нам сбалансировать химические уравнения, рассчитать количество продуктов и определить, будут ли реакции самопроизвольными. Вся наша система стехиометрии основана на истинности этих законов. Цель этого лабораторного эксперимента — проверить первый из этих законов, Закон сохранения массы. Если бы вы планировали эксперимент, чтобы подтвердить этот закон, вы бы хотели наблюдать две вещи: 1) имеет место реакция; 2) Суммарная масса всех реагентов равна (в пределах погрешности эксперимента) суммарной массе всех продуктов.  Поскольку реакция сульфата меди (II) и металлического цинка в водном растворе HCl полезна для наших целей, так как она вызывает как изменение цвета, так и выделение газа. За реакцией можно следить, наблюдая за потерей синей окраски раствора, выделением газообразного водорода и образованием твердой меди.  Путем количественного определения реагентов и продуктов этой реакции мы сможем подтвердить, что общая масса осталась неизменной (в пределах ошибки эксперимента), а также визуально подтвердить, что реакция действительно произошла. Как всегда в лаборатории, наряду с изучением новой концепции служат и другие цели. Мы также вернемся к использованию аналитических весов и приготовим наш первый химический раствор. Вы заметите, что фраза «в пределах экспериментальной ошибки» используется пару раз выше. Это связано с тем, что в любом эксперименте теряется определенное количество реагента и продукта, когда они переносятся из колбы в колбу или проливаются, разбрызгиваются или падают как часть человеческой ошибки в эксперименте. Эти «ошибки» необходимо учитывать при сообщении результатов любого эксперимента. Статистические данные часто используются для указания относительной важности ошибки. Например, потеря 100 граммов продукта может показаться огромной, если не сравнивать ее с ожидаемой массой продукта 2,5 x 106 г. Путем количественного определения реагентов и продуктов этой реакции мы сможем подтвердить, что общая масса осталась неизменной (в пределах ошибки эксперимента), а также визуально подтвердить, что реакция действительно произошла. Как всегда в лаборатории, наряду с изучением новой концепции служат и другие цели. Мы также вернемся к использованию аналитических весов и приготовим наш первый химический раствор. Вы заметите, что фраза «в пределах экспериментальной ошибки» используется пару раз выше. Это связано с тем, что в любом эксперименте теряется определенное количество реагента и продукта, когда они переносятся из колбы в колбу или проливаются, разбрызгиваются или падают как часть человеческой ошибки в эксперименте. Эти «ошибки» необходимо учитывать при сообщении результатов любого эксперимента. Статистические данные часто используются для указания относительной важности ошибки. Например, потеря 100 граммов продукта может показаться огромной, если не сравнивать ее с ожидаемой массой продукта 2,5 x 106 г.
|
Сохранение энергии — Энциклопедия Нового Света
- Эта статья о законе сохранения энергии в физике.
В физике закон сохранения энергии утверждает, что общее количество энергии в изолированной системе остается постоянным. На основании этого закона ученые пришли к выводу, что в изолированной системе энергия не создается и не уничтожается, но может менять форму. Например, потенциальная энергия может быть преобразована в кинетическую энергию, а кинетическая энергия может стать тепловой энергией.
Содержание
- 1 История
- 2 Первый закон термодинамики
- 3 Механика
- 3.1 Теорема Нётер
- 3.2 Относительность
- 3.3 Квантовая теория
- 4 См. также
- 5 Примечания
- 6 Каталожные номера
- 7 кредитов
Понимая этот закон, инженеры могут проектировать машины, которые могут использовать энергию для производства работы. Например, тепловая энергия (или тепло, выделяемое при сжигании топлива) может использоваться для привода турбины, которая, в свою очередь, может использоваться для выработки электроэнергии. Кроме того, на основании этого закона можно сделать вывод, что вечные двигатели могут работать только в том случае, если они не отдают энергию в окружающую среду, а устройства, производящие больше энергии, чем в них вложено, невозможны. Однако с формулировкой Альбертом Эйнштейном специальной теории относительности ученые теперь рассматривают сохранение энергии как часть более крупного закона, а именно сохранения «массы-энергии».
История
Древние философы догадывались о сохранении некой основной субстанции, из которой все сделано. Например, Фалес Милетский думал, что это вода.
В 1638 году Галилей опубликовал свой анализ нескольких ситуаций, включая знаменитый «прерванный маятник», которые можно описать (на современном языке) как консервативное преобразование потенциальной энергии в кинетическую и обратно. Однако Галилей не изложил этот процесс в современных терминах, и ему снова нельзя приписать решающее понимание. Это был Готфрид Вильгельм Лейбниц в 1676–1689 гг.{2}}
сохранялся до тех пор, пока массы не взаимодействовали. Он назвал это количество vis viva или жизненной силой системы. Принцип представляет собой точную формулировку приблизительного сохранения кинетической энергии в ситуациях, когда нет трения. Многие физики того времени считали, что закон сохранения импульса, сохраняющийся даже в системах с трением, определяемый импульсом:
- ∑imivi{\displaystyle \,\!\sum _{i}m_{i}v_{i}}
был законсервированным vis viva
 Позже было показано, что при соответствующих условиях обе величины сохраняются одновременно, например, при упругих столкновениях.
Позже было показано, что при соответствующих условиях обе величины сохраняются одновременно, например, при упругих столкновениях. В основном инженеры, такие как Джон Смитон, Питер Юарт, Карл Хоцманн, Гюстав-Адольф Хирн и Марк Сеген, возражали против того, что одного сохранения импульса недостаточно для практических расчетов, и использовали принцип Лейбница. Этот принцип также отстаивали некоторые химики, такие как Уильям Хайд Волластон. Такие академики, как Джон Плейфер, поспешили указать, что кинетическая энергия явно не сохраняется. Это очевидно для современного анализа, основанного на втором законе термодинамики, но в восемнадцатом и девятнадцатом веках судьба потерянной энергии была еще неизвестна. Постепенно возникло подозрение, что теплота, неизбежно генерируемая движением при трении, представляет собой другую форму vis viva . В 1783 году Антуан Лавуазье и Пьер-Симон Лаплас рассмотрели две конкурирующие теории vis viva и теорию калорийности. [1] Наблюдения графа Румфорда в 1798 г. за выделением тепла во время сверления пушек добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно) что преобразование было количественным и его можно было предсказать (с учетом универсальная константа преобразования между кинетической энергией и теплотой). 9{2}}
за выделением тепла во время сверления пушек добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно) что преобразование было количественным и его можно было предсказать (с учетом универсальная константа преобразования между кинетической энергией и теплотой). 9{2}}
, который можно понимать как нахождение точного значения константы преобразования кинетической энергии в работу, в значительной степени является результатом работы Гаспара-Гюстава Кориолиса и Жана-Виктора Понселе в период 1819–1839 гг. Первый назвал количество quantité de travail (количество работы), а второй travail mécanique (механическая работа), и оба отстаивали его использование в инженерных расчетах.
В газете, Über die Natur der Wärme, , опубликованном в Zeitschrift für Physik в 1837 году, Карл Фридрих Мор дал одно из первых общих утверждений доктрины сохранения энергии в следующих словах: «Кроме 54 известных химических элементов, в физическом мире существует только один агент , и это называется Kraft [энергия или работа]. В зависимости от обстоятельств она может проявиться как движение, химическое сродство, сцепление, электричество, свет и магнетизм, и из любой из этих форм она может быть преобразована в любую из другие.»
В зависимости от обстоятельств она может проявиться как движение, химическое сродство, сцепление, электричество, свет и магнетизм, и из любой из этих форм она может быть преобразована в любую из другие.»
Ключевым этапом в развитии современного принципа сохранения стала демонстрация механического эквивалента тепла . Калорическая теория утверждала, что теплота не может быть ни создана, ни уничтожена, но сохранение энергии влечет за собой противоположный принцип, согласно которому теплота и механическая работа взаимозаменяемы.
Принцип механической эквивалентности был впервые сформулирован в его современной форме немецким хирургом Юлиусом Робертом фон Майером. [2] Майер пришел к такому выводу во время путешествия в Голландскую Ост-Индию, где он обнаружил, что кровь его пациентов была более ярко-красной, потому что они потребляли меньше кислорода и, следовательно, меньше энергии для поддержания температуры тела в более жарких условиях. климат. Он обнаружил, что и теплота, и механическая работа являются формами энергии, а позже, улучшив свои познания в физике, вычислил количественную связь между ними.
Прибор Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикрепленный к веревке, заставляет вращаться весло, погруженное в воду.
Между тем, в 1843 году Джеймс Прескотт Джоуль независимо открыл механический эквивалент в серии экспериментов. В самом известном из них, ныне называемом «аппаратом Джоуля», опускающийся груз, прикрепленный к струне, заставлял вращаться лопасть, погруженную в воду. Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, равна тепловой энергии (теплу), приобретаемой водой при трении о весло.
В период 1840–1843 гг. подобную работу выполнял инженер Людвиг А. Колдинг, хотя она была малоизвестна за пределами его родной Дании.
Работа Джоуля и Майера страдала от сопротивления и пренебрежения, но именно работа Джоуля, возможно, несправедливо, в конечном итоге получила более широкое признание.
В 1844 году Уильям Роберт Гроув постулировал взаимосвязь между механикой, теплом, светом, электричеством и магнетизмом, рассматривая их все как проявления единой «силы» ( энергия по современным меркам). Гроув опубликовал свои теории в своей книге «Корреляция физических сил ». [3] В 1847 году, опираясь на более ранние работы Джоуля, Сади Карно и Эмиля Клапейрона, Герман фон Гельмгольц пришел к выводам, сходным с выводами Гроува, и опубликовал свои теории в своей книге Über die Erhaltung der Kraft ( On the Conservation Силы, 1847). Общее современное признание этого принципа проистекает из этой публикации.
Гроув опубликовал свои теории в своей книге «Корреляция физических сил ». [3] В 1847 году, опираясь на более ранние работы Джоуля, Сади Карно и Эмиля Клапейрона, Герман фон Гельмгольц пришел к выводам, сходным с выводами Гроува, и опубликовал свои теории в своей книге Über die Erhaltung der Kraft ( On the Conservation Силы, 1847). Общее современное признание этого принципа проистекает из этой публикации.
В 1877 году Питер Гатри Тейт утверждал, что этот принцип был создан сэром Исааком Ньютоном на основе творческого прочтения предложений 40 и 41 Philosophiae Naturalis Principia Mathematica . Сейчас это обычно рассматривается как не более чем пример истории вигов.
Первый закон термодинамики
Энтропия есть функция количества теплоты, которая показывает возможность преобразования этого тепла в работу.
Для термодинамической системы с фиксированным числом частиц первый закон термодинамики можно сформулировать так:
- δQ = dU + δW {\ displaystyle \ delta Q = \ mathrm {d} U + \ delta W \,} или эквивалентно, dU = δQ−δW {\ displaystyle \ mathrm {d} U = \ delta Q- \ delta W \,},
, где δQ {\ displaystyle \ delta Q} — количество энергии, добавляемой в систему в процессе нагрева, δ W {\ displaystyle \ delta W} — количество энергии, теряемой системой. из-за работы, совершаемой системой над ее окружением, и представляет собой увеличение внутренней энергии системы.
из-за работы, совершаемой системой над ее окружением, и представляет собой увеличение внутренней энергии системы.
Значения δ перед терминами тепла и работы используются для обозначения того, что они описывают приращение энергии, которое следует интерпретировать несколько иначе, чем приращение внутренней энергии. Работа и тепло равны обрабатывает , которые добавляют или вычитают энергию, в то время как внутренняя энергия представляет собой конкретную форму энергии, связанную с системой. Таким образом, термин «тепловая энергия» для δQ {\ displaystyle \ delta Q} означает «количество энергии, добавленное в результате нагрева», а не относится к конкретной форме энергии. Точно так же термин «рабочая энергия» для δW {\ displaystyle \ delta W} означает «то количество энергии, которое теряется в результате работы». Наиболее важным результатом этого различения является тот факт, что можно ясно указать количество внутренней энергии, которой обладает термодинамическая система, но нельзя сказать, сколько энергии поступило в систему или вышло из нее в результате ее нагревания или охлаждения. , ни в результате работы, выполняемой системой или системой. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.
, ни в результате работы, выполняемой системой или системой. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.
Для простой сжимаемой системы работа, выполненная системой, может быть записана
- δW=PdV{\displaystyle \delta W=P\,\mathrm {d} V},
где P{\displaystyle P} — давление, а dV{\displaystyle dV} — небольшое изменение объем системы, каждый из которых является системной переменной. Тепловая энергия может быть записана
- δQ = TdS {\ displaystyle \ delta Q = T \, \ mathrm {d} S},
, где T {\ displaystyle T} — температура, а dS {\ displaystyle \ mathrm {d} S} небольшое изменение энтропии системы. Температура и энтропия также являются системными переменными. 9{N} p_ {i} {\ dot {q}} _ {i} -L = const} и pi = ∂L ∂q˙i {\ displaystyle p_ {i} = {\ frac {\ partial L} {\ частичное {\dot {q}}_{i}}}}
, где L — функция Лагранжа. Чтобы эта конкретная форма была действительной, должно выполняться следующее:
- Система склерономная (ни кинетическая, ни потенциальная энергия не являются явной функцией времени)
- Кинетическая энергия представляет собой квадратичную форму относительно скоростей
- Потенциальная энергия не зависит от скорости
Теорема Нётер
Сохранение энергии является общей чертой многих физических теорий. С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждой симметрии физической теории соответствует сохраняющаяся величина; если симметрия теории инвариантна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. Философски это можно сформулировать так: «ничто не зависит от времени как такового».
Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонической величиной, сопряженной времени) сохраняется. И наоборот, теории, не инвариантные относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не обнаруживают сохранения энергии, если только не считать, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариантен во времени.
С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждой симметрии физической теории соответствует сохраняющаяся величина; если симметрия теории инвариантна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. Философски это можно сформулировать так: «ничто не зависит от времени как такового».
Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонической величиной, сопряженной времени) сохраняется. И наоборот, теории, не инвариантные относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не обнаруживают сохранения энергии, если только не считать, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариантен во времени. Поскольку любая меняющаяся во времени теория может быть встроена в инвариантную во времени метатеорию, сохранение энергии всегда можно восстановить путем подходящего переопределения того, что такое энергия. Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).
Поскольку любая меняющаяся во времени теория может быть встроена в инвариантную во времени метатеорию, сохранение энергии всегда можно восстановить путем подходящего переопределения того, что такое энергия. Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).
Относительность
С формулировкой специальной теории относительности Альбертом Эйнштейном энергия была предложена как один компонент 4-вектора энергии-импульса. Каждая из четырех составляющих (одна из энергии и три из импульса) этого вектора отдельно сохраняется в любой заданной инерциальной системе отсчета. Также сохраняется длина вектора (норма Минковского), которая является массой покоя. Релятивистская энергия одиночной массивной частицы содержит член, связанный с ее массой покоя, в дополнение к ее кинетической энергии движения. В пределе нулевой кинетической энергии (или, что то же самое, в системе покоя массивной частицы или в системе центра импульса для объектов или систем) полная энергия частицы или объекта (включая внутреннюю кинетическую энергию в системах) связана к его массе покоя через известное уравнение E=mc2{\displaystyle E=mc^{2}}. Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, также называемого 9-м правилом.0081 сохранение массы и энергии, сохранение массы-энергии, сохранение энергии-импульса, сохранение инвариантной массы, или сейчас обычно просто называют сохранением энергии.
Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, также называемого 9-м правилом.0081 сохранение массы и энергии, сохранение массы-энергии, сохранение энергии-импульса, сохранение инвариантной массы, или сейчас обычно просто называют сохранением энергии.
В общей теории относительности сохранение энергии-импульса выражается с помощью псевдотензора напряжения-энергии-импульса.
Квантовая теория
В квантовой механике энергия определяется как пропорциональная производной по времени волновой функции. Отсутствие коммутации оператора производной по времени с самим оператором времени математически приводит к принципу неопределенности для времени и энергии: чем больше период времени, тем точнее можно определить энергию (энергия и время становятся сопряженной парой Фурье).
Однако существует глубокое противоречие между исторической оценкой квантовой теорией плотности энергии вакуума во Вселенной и энергией вакуума, предсказанной космологической постоянной. Расчетная разница плотности энергии составляет порядка 10 120 раз. Складывается консенсус в отношении того, что полученная квантовой механикой плотность энергии поля в нулевой точке не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами в физике предпринимаются интенсивные усилия, чтобы решить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.
Расчетная разница плотности энергии составляет порядка 10 120 раз. Складывается консенсус в отношении того, что полученная квантовой механикой плотность энергии поля в нулевой точке не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами в физике предпринимаются интенсивные усилия, чтобы решить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.
См. также
- Теория хаоса
- Термодинамика
- Принцип неопределенности
- Закон сохранения
- Сохранение массы
- Энергетический баланс подземных вод
- Законы термодинамики
- Теорема Нётер
- Основы энергетики
- Преобразование энергии
- Качество энергии
Примечания
- ↑ А.Л. Лавуазье и П.С. Лаплас, Мемуары о тепле, Académie Royale des Sciences (1780): 4-355.
- ↑ Дж. Р. фон Майер, Замечания о силах неорганической природы, Annalen der Chemie und Pharmacie 43 (1842): 233.

- ↑ В. Р. Гроув, Корреляция физических сил, 6-е изд. (Лондон, Великобритания: Longmans, Green, 1874 г.).
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Brown, T.M. 1965. Информационное письмо EEC-1 об эволюции энергетических концепций от Галилея до Гельмгольца. Американский журнал физики . 33: 759–765.
- Кардуэлл, Д.С.Л. 1971. От Ватта до Клаузиуса: рост термодинамики в раннеиндустриальную эпоху . Лондон, Великобритания: Хайнеманн. ISBN 0435541501.
- Colding, LA 1864. К истории принципа сохранения энергии. Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 27: 56–64.
- Гольдштейн, Мартин и Ф. Инге Ф. 1993. Холодильник и Вселенная . Кембридж, Массачусетс: Гарвардский ун-т. Нажимать. ISBN 9780674753242.
- Guillen, M. 1999. Пять уравнений, изменивших мир . Лондон, Великобритания: Абакус. ISBN 0349110646.

- Хиберт, Э.Н. 1981. Исторические корни принципа сохранения энергии . Мэдисон, Висконсин: Паб Ayer Co. ISBN 0405138806.
- Кремер, Герберт и Чарльз Киттель. 1980. Теплофизика, 2-е изд. Сан-Франциско, Калифорния: W.H. Компания Фримен. ISBN 0716710889.
- Кун, Т.С. 1957. «Сохранение энергии как пример одновременного открытия». В М. Клагетт (ред.), Критические проблемы истории науки . Мэдисон, Висконсин: Издательство Висконсинского университета.
- Ланцос, Корнелиус. 1970. Вариационные принципы механики . Торонто, Калифорния: University of Toronto Press. ISBN 0802017436.
- Мах, Э. 1872. История и корни принципов сохранения энергии . Анн-Арбор, Мичиган: University Microfilms International.
- Нолан, Питер Дж. 1996. Основы физики колледжа, 2-е изд. Дубьюк, Айова: Издательство Уильяма К. Брауна. ISBN 9780697121455.
- Окстоби, Дэвид В. и Норман Х. Нахтриб. 1996. Принципы современной химии, 3-е изд.
 Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.
Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049. - Папино, Д. 2002. Размышление о сознании . Оксфорд, Великобритания: Издательство Оксфордского университета. ISBN 9780199271153.
- Пуанкаре, Х. 1905. Наука и гипотеза . Нью-Йорк, штат Нью-Йорк: репринт Дувра, 1952. ISBN 0486602214.
- Сартон, Г. 1929. Открытие закона сохранения энергии. Исида 13: 18–49.
- Серуэй, Рэймонд А. и Джон В. Джуэтт. 2004. Физика для ученых и инженеров, 6-е изд. Бельмонт, Калифорния: Брукс/Коул. ISBN 0534408427.
- Smith, C. 1998. Наука об энергии: культурная история физики энергии в викторианской Британии . Лондон, Великобритания: Хайнеманн. ISBN 0485114313.
- Стенгер, Виктор Дж. 2000. Вневременная реальность . Амхерст, Нью-Йорк: Книги Прометея. ISBN 9781573928595.
- Типлер, Пол. 2004. Физика для ученых и инженеров: механика, колебания и волны, термодинамика, 5-е изд.

 В наиболее сжатой форме он гласит:
В наиболее сжатой форме он гласит: 

 Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.
Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.