Разное

Метод люшера: Восьмицветовой тест Люшера — Пройти онлайн тест

ОпубликованоАвторalexxlab

Проходим тест Люшера (8 цветных карточек) — public void balaenrex скобки на DTF

Тест Люшера помогает оценить ваше текущее состояние, отношение к другим людям, понять, что вы чувствуете в данный момент, а также: характеристику воли, самооценку, возбудимость (HORNY), импульсивность, ожидания и отношение к окружению.

438 просмотров

Сам тест очень необычный, в нём нет вопросов и всего того, что ваш разум может выдать вместо вас. Все ваши действия будут диктоваться исключительно подсознанием. А оно реже врёт (или никогда).

Внимательно прочитайте правила выбора цветовых карточек. И (!!!) не думайте над ними долго. Вся соль — поддаваться первому импульсу, истинному желанию, из глубины.

Сейчас расслабьтесь, подумайте о своём текущем состоянии несколько секунд.

Добрий вечір, я зі Швеції. Що я повинен відповісти?

Интерпретация цветовых выборов

Характеристика общего настроения

Устремление + возбудимость + жажда перемен.

Вы стремитесь вырваться из ситуации, воспринимаемой Вами как парализующее ущемление, с тем, чтобы освободиться от всего излишнего и пережить сильное возбуждение, более не сдерживая себя. (**)

Стремления, мотивированные самопониманием

Вы не в состоянии далее справляться с избытком волнений и затруднений. Порой приходите в отчаяние и тешите себя мыслью о возможности порвать с мучительной ситуацией. Вы хотели бы поскорее освободиться и обрести долгожданное облегчение.

Эмоциональное отношение к высокозначимым лицам

Вы противитесь сердечной привязанности и всеми силами оберегаете собственную независимость. В отношениях с партнером Вы последовательно соблюдаете дистанцию и демонстративно требуете подчеркнутого уважения к себе. Критика других рассматривается Вами как метод эффективной защиты своих интересов.

Характеристика воли и самооценка

Вы не признаете условностей и норм установленного порядка, не любите принимать окончательных решений хотя бы ради того, чтобы после не приходилось со смущением от них отказываться.

Вы хотите быть оригинальным человеком, а потому во всем и везде ищете экстравагантных решений и чарующих встреч.

Возбудимость и импульсивность

Вы чувствуете, что должны продолжать борьбу с пренебрежительным к себе отношением и открытой эксплуатацией другими. К несправедливым требованиям окружения и партнера Вы испытываете явное отвращение, а потому занимаете выражено оборонительную позицию. До сих пор Вам удается сдерживать возбуждение и агрессивность, однако из-за этого Вы теряете спонтанность и становитесь чересчур возбудимым.

Ожидания и отношение к окружению

Вы усиленно стремитесь установить непосредственный и безоговорочный контакт с близкими людьми. К чувственной стороне отношений Вы проявляете немалый интерес и искренно радуетесь всем неожиданным телесным переживаниям.

Желаемые цели и средства эмоционального поведения; устремления и защитное эмоциональное поведение

Ожидание + готовность к увлечениям. Ваша склонность к фантазированию и мечтаниям и стремление к интересным и волнующим событиям направлены на удовлетворение потребности в признании и восхищении окружающих. Вы обладаете слишком развитым воображением и безоглядно погружаетесь в фантазии и мечты. Жаждете удивить других Вашей неотразимостью и обаянием. Вы тоскуете по приятным содержательным встречам и жаждете чарующей любви. Активно развиваете фантазийные представления о будущем и замещаете ими реальную оценку происходящего. (*)

Существующее эмоциональное положение, текущее состояние, собственно настрой, уместное эмоциональное поведение

Вы стремитесь к спокойной и прочной привязанности и единению, чтобы чувствовать себя признанным, ценимым, любимым и довольным. Желаете обрести спокойную и твердую уверенность в себе, подкрепляемую открытыми выражениями уважения других. Вы аккуратны, методичны и самостоятельны, нуждаетесь в признании сотрудников и понимании со стороны близких. Вам необходима постоянная эмоциональная поддержка окружения.

Сдерживаемые качества, временно утраченные свойства, отложенные возможности, ограничиваемые, воспринимаемые как неуместные и находящиеся в резерве

Для Вас характерны отсутствие желаний и безрадостность. Вы чувствуете, что другие мешают Вам реализовать себя и чинят препятствия на пути раскрытия способностей. Это вконец Вас измучило. Вы ищете покоя, избегаете конфликтов и прямых столкновений и намерены в дальнейшем щадить себя, отказываясь от перенапряжения. Испытываете тревогу и апатию, Вам кажется, что Вы окружены неприятелями со всех сторон. Вы полагаете, что сами обстоятельства вынуждают Вас сдерживать свои желания. Вы чувствуете, что попали в затруднительное положение, но усердно избегаете открытых конфликтов.

Источники неосознаваемой тревожности; потребности, затормаживаемые ввиду нецелесообразности

Перераздражение способности воспринимать переживаемое + отклонение помех и неприятие ограничений. Первичное действие: стресс вызван разочарованиями, вошедшими в жизнь вместе с какой-то нежелательной ситуацией.

Психологически: Вы чувствуете, что попали в неприятную ситуацию, мучительную и тяжкую, исправить которую Вы бессильны. Вы рассержены и раздражены из-за сомнений в возможности достижения собственных целей. Вы фрустрированы вплоть до нервного истощения. Хотите освободиться от этого мучительного состояния, чтобы избежать помех и свободно действовать согласно собственным убеждениям. Вы хотите выпутаться из создавшейся ситуации и обрести возможность свободно принимать решения. (Цветопара в начале ряда указывает на характер компенсации.) Коротко: фрустрированное желание независимости. (

*)

Актуальная эмоциональная проблема

Вы чувствуете недостаток уважения, а потому ищете различные ситуации, в которых можно было бы продемонстрировать окружающим свои достоинства.

Восхищение перед необычным и оригинальным, перед людьми, наделенными талантом, вызывает у Вас попытки перенять эти качества с тем, чтобы и самому быть выдающимся.

Тревожность и внутренние конфликты

Показатель тревожности: 1 из 12 – незначительная тревожность. (I AM HORNY!)

Пункты со звездочками указывают на наличие внутреннего конфликта.

Одна звездочка (*) показывает наличие конфликта, но он не обязательно носит серьезный характер.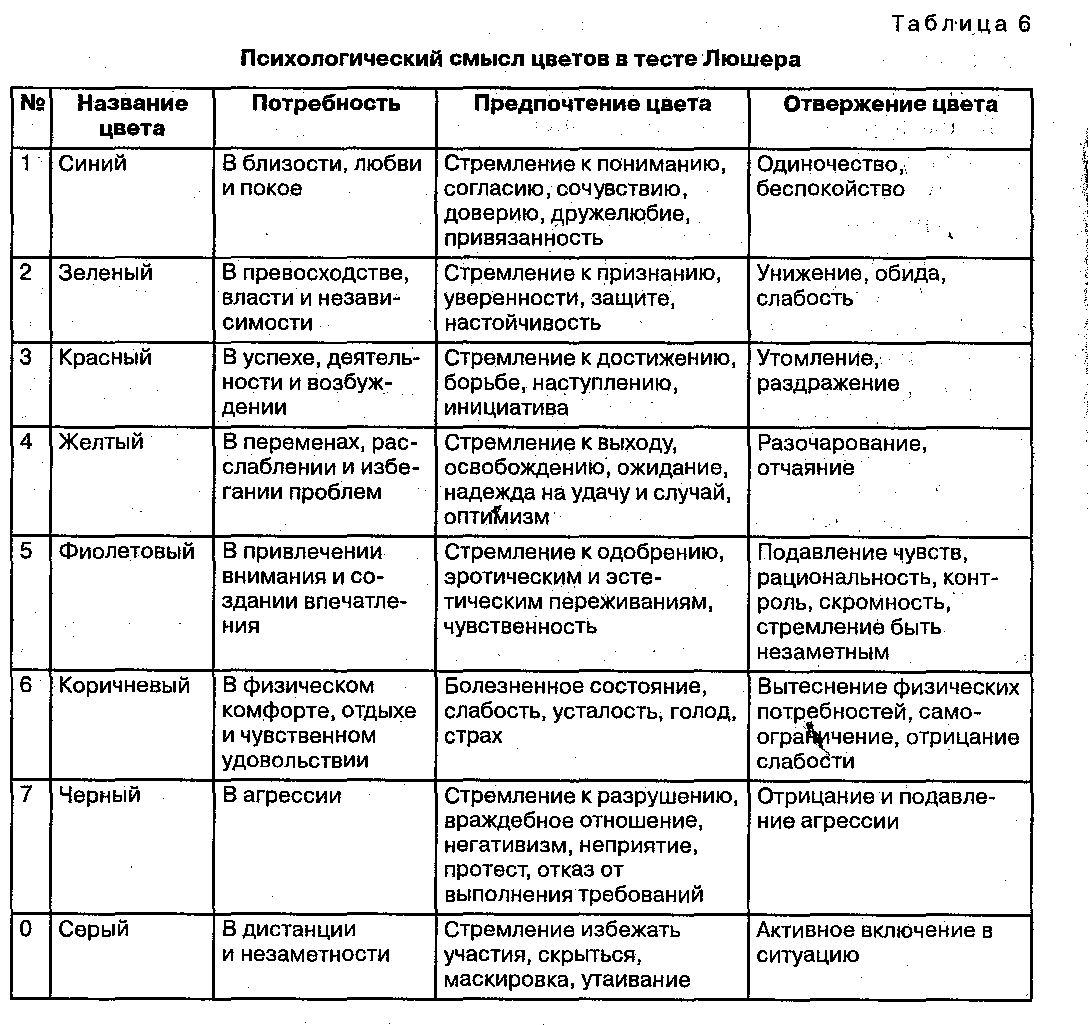

Две звездочки (**) свидетельствуют о наличии ощутимого конфликта.

Три звездочки (***) – это серьезный внутренний конфликт.

Психологический тест Люшера — узнай свой психотип

ПсихологияЮмор и Развлечения

Этот простой тест на определение психологического состояния человека изобрел в 1948 году Макс Люшер. Данное событие было переворотом в области психологии и психиатрии. Метод успешно используется и современными врачами, мало того его можно сделать самостоятельно.

Что он из себя представляет? Ниже вы видите рисунок, на нем изображены 8 прямоугольников разных цветов. Вы выбираете один из них. Важно, чтобы во время выбора вы не руководствовались ничем кроме подсознания. Это не должен быть ваш любимый цвет, или какие-то предпочтения в одежде, вы не должны заглядывать в значения цветов. Расслабьтесь, посмотрите на рисунок и выберите тот прямоугольник, цвет которого вам нравится на данный момент.

Значения цветов:

— Если вы выбрали ЧЕРНЫЙ — вам знакомо чувство одиночества, но вы умеете с ним справляться. Вы стараетесь не показывать своих слабых сторон, хотя в тайне мечтаете о том, чтобы кто-то о вас позаботился ,взял ответственность. Вы решаете все проблемы в одиночку, имеете свое мнение, и не подвержены влиянию других людей.

— Если вы выбрали СЕРЫЙ — вы очень вдумчивый человек – «семь раз отмерь – один раз отрежь» — это про вас. Стараетесь не выделяться из толпы, но у вас богатый внутренний мир. Вы душевны, мягки, скромны. Это доставляет вам немало переживаний, иногда порождает неуверенность в себе. Не сомневайтесь, просто добавьте в свою жизнь немного красок.

— Если вы выбрали КРАСНЫЙ — вы натура страстная, целеустремленная, эмоциональная. Для вас вполне вероятны яркие всплески эмоций – от всеобъемлющей любви до лютой ненависти. Вы можете обидеть кого-то ненароком, но совершенно не подозревая об этом и не думая о последствиях. Вы умеете заряжать своей страстью окружающих, у вас огромный жизненный потенциал.

— Если вы выбрали КОРИЧНЕВЫЙ – вы практичный человек, совершенно не витающий в облаках. Вам важны факты и доказательства, а не идеи и мечты. В этом ваш большой плюс – вы живете «настоящим», реально оценивая свои возможности. Минус состоит в том, что вам сложно выйти за рамки, совершить что-то грандиозное или поверить во что-то невероятное.

— Если вы выбрали ЖЕЛТЫЙ – вы позитивны, открыты, коммуникабельны. Оптимизм – это ваше все. Вы умеете нравиться людям, с вами легко общаться. Вы имеете много увлечений, т.к. вам все интересно. Умеете радоваться простым вещам и восхищаться маленькими проявлениями добра в людях.

— Если вы выбрали СИНИЙ – вы само спокойствие. Вам важен психологический комфорт как в обстановке, так и в общении с людьми. Вы уверенны в себе, талантливы, стремитесь к гармонии. Вы очень глубокая натура, мечтатель, романтик, поэтому от житейской суеты и быта испытываете усталость.

-Если вы выбрали ЗЕЛЕНЫЙ — у вас есть все, чтобы добиться успеха – жажда жизни, целеустремленность, потенциал. Вы любите жизнь и все, что вас окружает. Стремитесь к своей цели. Но есть и минус – вы подвержены критике – если не чувствуете поддержки, теряете уверенность в себе.

-Если вы выбрали ФИОЛЕТОВЫЙ — вы любознательная, увлеченная натура, склонная мистифицировать мир вокруг себя. Фиолетовый объединяет в себе противоположности, как и сам человек. Вы человек настроения — у вас бывают резкие переходы от активности к полному безразличию, из крайности в крайность, но в душе вы стремитесь к гармонии. Такой цвет часто выбирают натуры творческие.

из feellfeed.pw

Tags:психотип, тест, цвет

Прошлый пост 10 фильмов, которые перетрут ваш жизненный опыт в порошок

Следующий пост 14 фильмов, которые изменили в этом мире что-то раз и навсегда

Согласованность между методом конечных объемов Люшера и методом HAL КХД для двухбарионных систем в решеточной КХД

Согласованность между методом конечных объемов Люшера и методом HAL КХД для двухбарионных систем в решеточной КХД

Скачать PDF

Скачать PDF

  • Обычная статья — Теоретическая физика
  • Открытый доступ
  • Опубликовано:
  • Сотрудничество HAL QCD,
  • Такуми Иритани 1 ,
  • Синья Аоки 2,3 ,
  • Такуми Дои 1,4 ,
  • Тецуо Хацуда 1,4 ,
  • Ёити Икеда 5 ,
  • Такаси Иноуэ 6 ,
  • Нориёси Исии 5 ,
  • Хидэкацу Немура 5 и
  • …
  • Кенджи Сасаки 2  

Журнал физики высоких энергий том 2019 , Номер статьи: 7 (2019) Процитировать эту статью

  • 373 доступа

  • 22 Цитаты

  • 1 Альтметрика

  • Сведения о показателях

Аннотация

Существует два метода изучения двухбарионных систем в решеточной КХД: прямой метод, который извлекает собственные энергии из плато временной корреляционной функции, и метод HAL КХД, который извлекает наблюдаемые из нелокального потенциала, связанного с пространственно-временным корреляционная функция. Хотя теоретически эти два метода должны давать одинаковые результаты, сообщалось о качественном различии наблюдаемых данных при моделировании КХД на решетке. Недавно мы указали в [1, 2], что отделение основного состояния от возбужденных состояний имеет решающее значение для получения разумных результатов в первом, в то время как оба состояния обеспечивают полезные сигналы для наблюдаемых во втором. В этой статье мы идентифицируем вклад каждого состояния в прямом методе путем разложения двухбарионных корреляционных функций на собственные моды конечного объема, полученные методом HAL КХД. Как и в наших предыдущих исследованиях, мы рассматриваем систему ΞΞ в 1 S 0 канал на м π = 0,51 ГэВ в (2+1)-ароматной решетке КХД с использованием пристеночных и размытых источников кварков с пространственной протяженностью, La = 3. 6, 4.3, 5.8 фм. Показано, что «псевдоплато» на ранних временных срезах ( t = 1 ∼ 2 фм) от размытого источника в прямом методе действительно возникает из-за контаминации возбужденных состояний, а плато с насыщением основного состояния реализовано только на т > 5 ∼ 15 фм, что соответствует обратной величине наименьшей энергии возбуждения. Мы также показываем, что двухбарионный оператор можно оптимизировать, используя собственные моды конечного объема, так что (i) энергетические спектры конечного объема из метода HAL КХД согласуются со спектрами временной корреляционной функции с оптимизированными операторами и ( ii) правильные спектры конечного объема будут доступны в прямом методе только в том случае, если используются высокооптимизированные операторы. Таким образом, мы заключаем, что давний вопрос о согласованности между методом конечных объемов Люшера и методом HAL КХД для двух барионов в настоящее время решен, по крайней мере, для этой конкретной системы, рассматриваемой здесь: они согласуются друг с другом количественно только в том случае, если возбужденное загрязнение правильно удалены в бывшем.

Скачайте, чтобы прочитать полный текст статьи

Ссылки

  1. Сотрудничество HAL QCD, T. Iritani et al., Mirage in Temporal Correlation functions for Baryon-Baryon Interactions in Lattice QCD , JHEP 10 (2016) 101 [arXiv:1607.06371] [ВДОХНОВЕНИЕ].

  2. Коллаборация HAL КХД, Т. Иритани и др., Связаны ли два нуклона в КХД на решетке для масс тяжелых кварков? Проверка непротиворечивости с помощью формулы конечного объема Люшера , Физ. Ред. D 96 (2017) 034521 [arXiv:1703.07210] [ВДОХНОВЕНИЕ].

  3. Т. Ямадзаки, К.-и. Ishikawa, Y. Kuramashi and A. Ukawa, Исследование зависимости энергии связи легких ядер от массы кварка в решетке аромата 2+1 КХД , Phys. Ред. D 92 (2015) 014501 [arXiv:1502.04182] [ВДОХНОВЕНИЕ].

    ОБЪЯВЛЕНИЕ Google Scholar

  4. NPLQCD коллаборация, М.Л. Wagman et al. , Барион-барионные взаимодействия и спин-ароматная симметрия из квантовой хромодинамики решетки , Phys. Ред. D 96 (2017) 114510 [arXiv:1706.06550] [ВДОХНОВЕНИЕ].

  5. Коллаборация CalLat, E. Berkowitz et al., Двухнуклонное рассеяние высших парциальных волн на решеточной КХД , Phys. лат. B 765 (2017) 285 [arXiv:1508.00886] [ВДОХНОВЕНИЕ].

  6. М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 1. Стабильные состояния частиц , Общ. Мат. физ. 104 (1986) 177 [ВДОХНОВЕНИЕ].

  7. М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 2. Состояния рассеяния , Общ. Мат. физ. 105 (1986) 153 [ВДОХНОВЕНИЕ].

  8. М. Люшер, Два состояния частиц на торе и их связь с матрицей рассеяния , Nucl. физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  9. Н. Исии, С. Аоки и Т. Хацуда, Ядерная сила из КХД решетки , Физ. Преподобный Летт. 99 (2007) 022001 [nucl-th/0611096] [INSPIRE].

  10. С. Аоки, Т. Хацуда и Н. Исии, Теоретические основы ядерных сил в КХД и их приложения к центральным и тензорным силам в КХД-моделировании закаленных решеток , Prog. Теор. физ. 123 (2010) 89 [arXiv:0909.5585] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  11. HAL Сотрудничество КХД, Н. Ишии и др., Адрон-адронные взаимодействия из волновой функции Намбу-Бете-Солпитера в мнимом времени на решетке , Phys. лат. B 712 (2012) 437 [arXiv:1203.3642] [ВДОХНОВЕНИЕ].

  12. Коллаборация HAL КХД, С. Аоки и др., Решетчатый подход КХД к ядерной физике , PTEP 2012 (2012) 01A105 [arXiv:1206.5088] [ВДОХНОВЕНИЕ].

  13. С. Аоки, КХД на решетке и ядерная физика , в Современные перспективы КХД на решетке: квантовая теория поля и высокопроизводительные вычисления. Proceedings, International School, 93rd Session , Les Houches, France, 3–28 августа 2009 г., стр. 591–628 (2010) [arXiv:1008.4427] [INSPIRE].

  14. Коллаборация NPLQCD, S.R. Beane et al., Легкие ядра и гиперядра из квантовой хромодинамики в пределе SU(3) Flavor Symmetry , Физ. Ред. D 87 (2013) 034506 [arXiv:1206.5219] [ВДОХНОВЕНИЕ].

  15. Сотрудничество HAL QCD, T. Inoue et al., Потенциалы двух барионов и H-дибарион из моделирования КХД с 3 ароматами , Nucl. физ. A 881 (2012) 28 [arXiv:1112.5926] [ВДОХНОВЕНИЕ].

  16. А. Фрэнсис, Дж. Р. Грин, П.М. Junnarkar, C. Miao, T.D. Rae and H. Wittig, Решеточная КХД, исследование дибариона H с использованием гексакваркового и двухбарионного интерполяторов , arXiv:1805.03966 [ВДОХНОВЕНИЕ].

  17. T. Iritani для коллаборации с HAL КХД, Барионные взаимодействия в решеточной КХД: прямой метод против потенциального метода HAL КХД , PoS(LATTICE2016)107 (2016) [arXiv:1610.09779] [INSPIRE].

  18. С. Аоки, Т. Дои и Т. Иритани, Проверка работоспособности связанных состояний NN в КХД решетки с формулой конечного объема Люшера — Раскрытие симптомов ложных плато — , EPJ Web Conf. 175 (2018) 05006 [arXiv:1707. 08800] [ВДОХНОВЕНИЕ].

    Артикул Google Scholar

  19. Т. Иритани для коллаборации с HAL КХД, Двухбарионные системы из метода HAL КХД и миража во временной корреляции прямого метода , EPJ Web Conf. 175 (2018) 05008 [arXiv:1710.06147] [ВДОХНОВЕНИЕ].

  20. Сотрудничество HAL QCD, T. Iritani et al., Систематика потенциала HAL КХД при низких энергиях в решеточной КХД , Phys. Ред. D 99 (2019) 014514 [arXiv:1805.02365] [ВДОХНОВЕНИЕ].

  21. Г. Паризи, Стратегия вычисления спектра адронных масс , Phys. Представитель 103 (1984) 203 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  22. Г.П. Lepage, The Analysis of Algorithms for Lattice Field Theory , in From Actions to Answers: Proceedings of the TASI 1989 , T. Degrand and D. Toussaint eds., World Scientific, Сингапур (1990) [CLNS-89-971 ] [ВДОХНОВЛЯТЬ].

  23. https://en.wikipedia.org/wiki/Sanity_check.

  24. К. Мурано, Н. Исии, С. Аоки и Т. Хацуда, Нуклон-нуклонный потенциал и его нелокальность в решетке КХД , Прогр. Теор. физ. 125 (2011) 1225 [arXiv:1103.0619] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  25. К. Нисидзима, Формулировка полевых теорий составных частиц , Phys. Ред. 111 (1958) 995 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

  26. W. Zimmermann, О проблеме связанного состояния в квантовой теории поля , Nuovo Cim. 10 (1958) 597 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

  27. Р. Хааг, Квантовые теории поля с составными частицами и асимптотическими условиями , Phys. Ред. 112 (1958) 669 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

  28. Т. Ямадзаки, К.-и. Исикава, Ю. Курамаси и А. Укава, Ядра гелия, дейтрон и динейтрон в решетке аромата 2+1 КХД , Физ. Ред. D 86 (2012) 074514 [arXiv:1207.4277] [ВДОХНОВЕНИЕ].

    ОБЪЯВЛЕНИЕ Google Scholar

  29. Т. Дои и М.Г. Эндрес, Единый алгоритм сжатия для мультибарионных корреляторов на решетке , Вычисл. физ. коммун. 184 (2013) 117 [arXiv:1205.0585] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  30. Коллаборация NPLQCD, K. Orginos et al., Две нуклонные системы на m π ∼ 450 МэВ из КХД на решетке , Физ. Ред. D 92 (2015) 114512 [arXiv:1508.07583] [ВДОХНОВЕНИЕ].

  31. Коллаборация NPLQCD, S.R. Beane et al., Комментарий к статье «Связаны ли два нуклона в решеточной КХД для масс тяжелых кварков? — Проверка работоспособности с помощью формулы конечного объема Люшера — , arXiv:1705.09239 [INSPIRE].

  32. М. Люшер и У. Вольф, Как рассчитать матрицу упругого рассеяния в двумерных квантовых теориях поля с помощью численного моделирования , Нукл. физ. B 339 (1990) 222 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  33. Р.А. Брицено, Дж.Дж. Дудек и Р.Д. Янг, Процессы рассеяния и резонансы в КХД на решетке , Rev. Mod. физ. 90 (2018) 025001 [arXiv:1706.06223] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  34. Сотрудничество HAL QCD, S. Gongyo et al., Самый странный дибарион из решетки QCD , Phys. Преподобный Летт. 120 (2018) 212001 [arXiv:1709.00654] [ВДОХНОВЕНИЕ].

  35. HAL КХД коллаборация, Т. Иритани и др., N Ω дибарион из решеточной КХД вблизи физической точки , arXiv:1810.03416 [INSPIRE].

  36. Сотрудничество HAL QCD, T. Inoue et al., Strange Nuclear Physics из КХД на решетке , in 13th International Conference on Hypernuclear and Strange Particle Physics (HYP 2018) , Портсмут, Вирджиния, США, 24–29 июня 2018 г. [arXiv:1809.08932] [INSPIRE].

  37. T. Amagasa et al., Совместное использование данных решетчатой ​​КХД в широко распространенной файловой системе , J. Phys. конф. сер. 664 (2015) 042058 [ВДОХНОВЕНИЕ].

    Артикул Google Scholar

  38. http://www.lqcd.org/ildg.

  39. http://www.jldg.org.

  40. Columbia Physics System (CPS), http://usqcd-software.github.io/CPS.html.

  41. Bridge++, http://bridge.kek.jp/Lattice-code/.

  42. М. Шрек и Х. Фогт, Фиксация кулоновской, ландауской и максимально абелевой калибровки в решеточной КХД с мульти-GPU , Вычисл. физ. коммун. 184 (2013) 1907 [arXiv:1212.5221] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

  43. T. Boku et al., Многоблочный/многоядерный предобуславливатель SSOR для кваркового решателя QCD для компьютера K , PoS(LATTICE2012)188 (2012) [arXiv:1210.7398] [INSPIRE].

  44. М. Терай и др., Настройка производительности решетчатого кода КХД на узле компьютера K (на японском языке), IPJ Trans. Доп. вычисл. Сист. 6 (2013) 43.

Скачать ссылки

Открытый доступ

Эта статья распространяется в соответствии с лицензией Creative Commons Attribution License (CC-BY 4. 0), которая разрешает любое использование, распространение и воспроизведение на любом носителе при условии указания автора(ов) и источника.

Информация об авторе

Авторы и организации

  1. RIKEN Nishina Center, Wako, 351-0198, Japan

    Takumi Iritani, Takumi Doi & Tetsuo Hatsuda

  2. Центр гравитационной физики, Институт теоретической физики им. Юкавы, K Университет Йото, Китасиракава Оивакечо, Сакё-ку, Киото, 606-8502, Япония

    Синья Аоки и Кенджи Сасаки

  3. Центр вычислительных наук Университета Цукуба, Цукуба, 305-8577, Япония

    Синья Аоки

    9 0010

  4. Междисциплинарная теоретико-математическая научная программа RIKEN (iTHEMS), Вако, 351-0198, Япония

    Такуми Дои и Тецуо Хацуда

  5. Исследовательский центр ядерной физики (RCNP), Осакский университет, Осака, 567-0 047, Япония

    Ёити Икэда, Нориёси Исии и Хидэкацу Немура

  6. Университет Нихон, Колледж наук о биоресурсах, Канагава, 252-0880, Япония

    Такаси Иноуэ

    7. 9053 3 Авторов

    1. Такуми Иритани

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    2. Sinya Aoki

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    3. Takumi Doi

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    4. Тецуо Хацуда

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    5. Yoichi Ikeda

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    6. Takashi Inoue

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    7. Noriyoshi Ishii

      Посмотреть публикации автора

      Вы также можете искать этого автора в PubMed Google Scholar

    8. Hidekatsu Nemura

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    9. Kenji Sasaki

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

    Консорциумы

    Сотрудничество HAL QCD

    Автор, ответственный за переписку

    Такуми Иритани.

    Дополнительная информация

    ArXiv ePrint: 1812.08539

    Права и разрешения

    Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе. или формат , при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и укажите, были ли внесены изменения.

    Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на эту статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя.

    Чтобы просмотреть копию этой лицензии, посетите https://creativecommons. org/licenses/by/4.0/.

    Перепечатка и разрешения

    Об этой статье

    Рассеяние двух частиц в условиях квантования конечного объема с использованием базиса плоских волн

  7. М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 1. Стабильные состояния частиц , Общ. Мат. физ. 104 (1986) 177 [ВДОХНОВЕНИЕ].

  8. М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 2. Состояния рассеяния , Комм. Мат. физ. 105 (1986) 153 [ВДОХНОВЕНИЕ].

  9. М. Люшер, Два состояния частиц на торе и их связь с матрицей рассеяния , Nucl. физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  10. К. Руммукайнен, С. А. Готтлиб, Фазовые сдвиги резонансного рассеяния на решетке не покоящегося каркаса , Нукл. физ. B 450 (1995) 397 [hep-lat/9503028] [INSPIRE].

  11. С. ч. Ким, С. Т. Сачрайда и С. Р. Шарп, Эффекты конечного объема для двухадронных состояний в движущихся системах отсчета , Nucl. физ. B 727 (2005) 218 ​​[hep-lat/0507006] [INSPIRE].

  12. M. Gokeler et al., Фазы рассеяния для мезонных и барионных резонансов на общих решетках с подвижной системой отсчета , Phys. Ред. D 86 (2012) 094513 [arXiv:1206.4141] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  13. T. Luu and M.J. Savage, Извлечение фазовых сдвигов рассеяния в более высоких парциальных волнах из расчетов КХД на решетке , Phys. Ред. D 83 (2011) 114508 [arXiv:1101.3347] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  14. Z. Fu, Формула Руммукайнена-Готлиба для двухчастичной системы с различной массой , Phys. Ред. D 85 (2012) 014506 [arXiv:1110.0319] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  15. Л. Лесковец и С. Преловсек, Фазовые сдвиги рассеяния для двух частиц с различной массой и ненулевым полным импульсом в решеточной КХД , Физ. Ред. D 85 (2012) 114507 [arXiv:1202.2145] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  16. Р. А. Брицено, Двухчастичные многоканальные системы в конечном объеме с произвольным спином , Физ. Ред. D 89 (2014) 074507 [arXiv:1401.3312] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  17. М. Лаге, У.-Г. Мейснер и А. Русецкий, Метод измерения длины рассеяния антикаона на нуклоне в решеточной КХД , Физ. лат. B 681 (2009) 439 [arXiv:0905.0069] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  18. S. He, X. Feng and C. Liu, Два состояния частиц и элементы S-матрицы в многоканальном рассеянии [ВДОХНОВЛЯТЬ].

  19. М. Т. Хансен и С. Р. Шарп, Многоканальное обобщение формулы Леллуша-Люшера , Физ. Ред. D 86 (2012) 016007 [arXiv:1204.0826] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  20. М. Деринг, У. Г. Мейснер, Э. Осет и А. Русецкий, Скалярные мезоны, движущиеся в конечном объеме, и роль парциального волнового смешивания , Eur. физ. J. A 48 (2012) 114 [arXiv:1205.4838] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  21. X. Feng, X. Li and C. Liu, Два состояния частиц в асимметричном ящике и фазы упругого рассеяния , Phys. Ред. D 70 (2004) 014505 [hep-lat/0404001] [INSPIRE].

  22. Р. А. Брицено, Дж. Дж. Дудек и Р. Д. Янг, Процессы рассеяния и резонансы в КХД на решетке , Rev. Mod. физ. 90 (2018) 025001 [arXiv:1706.06223] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  23. М. Май, М. Деринг и А. Русецкий, Многочастичные системы на решетке и киральные экстраполяции: краткий обзор , Eur. физ. J. ST 230 (2021) 1623 [arXiv:2103.00577] [INSPIRE].

    Артикул Google Scholar

  24. Х.-Х. Чен, В. Чен, С. Лю и С.-Л. Zhu, Пентакварковые и тетракварковые состояния со скрытым очарованием , Phys. Представитель 639 (2016) 1 [arXiv:1601. 02092] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  25. Ф.-К. Го, К. Ханхарт, У.-Г. Мейснер, К. Ван, К. Чжао и Б.-С. Zou, Адронные молекулы , Rev. Mod. физ. 90 (2018) 015004 [arXiv:1705.00141] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  26. N. Brambilla et al., Состояния X Y Z: экспериментальный и теоретический статус и перспективы , Физ. Представитель 873 (2020) 1 [arXiv:1907.07583] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  27. П. Ф. Бедак, И. Сато и А. Уокер-Лауд, Поправки на конечный объем к π-π рассеянию , Phys. Ред. D 73 (2006) 074501 [hep-lat/0601033] [INSPIRE].

  28. И. Сато и П. Ф. Бедак, Помещение двух нуклонов в ящик: экспоненциально подавленные поправки к формуле Люшера , Физ. Ред. D 76 (2007) 034502 [hep-lat/0702021] [INSPIRE].

  29. M. Jansen, H.W. Hammer and Y. Jia, Поправки на конечный объем к энергии связи X(3872) , Phys. Ред. D 92 (2015) 114031 [arXiv:1505.04099] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  30. М. Деринг, У.-Г. Мейснер, Э. Осет и А. Русецкий, Унитаризованная киральная теория возмущений в конечном объеме: скалярный мезонный сектор , Евро. физ. J. A 47 (2011) 139 [arXiv:1107.3988] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  31. З.-Х. Го, Л. Лю, У.-Г. Мейснер, Дж. А. Оллер и А. Русецкий, . Киральное исследование а- 0 (980) -резонанса и фазовых сдвигов πη-рассеяния в свете недавнего моделирования решетки , Phys. Ред. D 95 (2017) 054004 [arXiv:1609.08096] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  32. З.-Х. Го, Л. Лю, У.-Г. Мейснер, Дж. А. Оллер и А. Русецкий, К точному определению амплитуд рассеяния очарованных и светлых псевдоскалярных мезонов , Eur. физ. J. C 79 (2019) 13 [arXiv:1811.05585] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  33. M. Albaladejo, J.A. Oller, E. Oset, G. Rios and L. Roca, Обработка ππ-рассеяния в конечных объемах и пределы извлечения фазовых сдвигов из решеточной КХД , JHEP 08 (2012) 071 [arXiv :1205.3582] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  34. Х.-Х. Чен и Э. Осет, ππ-взаимодействие в ρ-канале в конечном объеме , Phys. Ред. D 87 (2013) 016014 [arXiv:1202.2787] [INSPIRE].

  35. Дж. М. М. Холл, А. С. П. Хсу, Д. Б. Лейнвебер, А. В. Томас и Р. Д. Янг, Матричная гамильтонова модель конечного объема для системы ∆ → Nπ , Phys. Ред. D 87 (2013) 094510 [arXiv:1303.4157] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  36. Ж.-Ж. Ву, Т. С. Х. Ли, А. В. Томас и Р. Д. Янг, Метод гамильтониана конечного объема для взаимодействий связанных каналов в решеточной КХД , Физ. Ред. C 90 (2014) 055206 [arXiv:1402.4868] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  37. Z.-W. Лю, В. Камле, Д. Б. Лейнвебер, Ф. М. Стоукс, А. В. Томас и Дж.-Дж. Wu, Теория эффективного поля Гамильтона исследование резонанса N ∗ ( 1535 ) в решеточной КХД , Phys. Преподобный Летт. 116 (2016) 082004 [arXiv:1512.00140] [INSPIRE].

  38. Ю. Ли, Дж.-Дж. Ву, Д. Б. Лейнвебер и А. В. Томас, Гамильтонова эффективная теория поля в удлиненном или движущемся конечном объеме , Phys. Ред. D 103 (2021) 094518 [arXiv:2103.12260] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  39. C. Morningstar et al., Оценка двухчастичной K-матрицы для множественных парциальных волн и каналов распада по энергиям конечного объема , Нукл. физ. B 924 (2017) 477 [arXiv:1707.05817] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  40. Ю. Ли, Дж.-Дж. Wu, CD Abell, DB Leinweber and AW Thomas, Парциальное смешивание волн в гамильтоновой теории эффективного поля , Phys. Ред. D 101 (2020) 114501 [arXiv:1910.04973] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  41. Ф. X. Ли, А. Александру и Р. Бретт, Проверка условия квантования конечного объема для двух бесспиновых частиц , arXiv:2107.04430 [INSPIRE].

  42. F. X. Lee, C. Morningstar and A. Alexandru, Энергетический спектр двухчастичного рассеяния в периодическом ящике , Int. Дж. Мод. физ. C 31 (2020) 2050131 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  43. R. A. Briceno, Z. Davoudi and T.C. Luu, Двухнуклонные системы в конечном объеме: (I) условия квантования , Phys. Ред. D 88 (2013) 034502 [arXiv:1305.4903] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  44. C. Morningstar et al., Расширенные адронные и двухадронные операторы определенного импульса для расчета спектра в решеточной КХД , Phys. Версия D 88 (2013) 014511 [arXiv:1303.6816] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  45. В. Бернар, М. Лаге, У.-Г. Мейснер и А. Русецкий, Резонансные свойства из энергетического спектра конечного объема , JHEP 08 (2008) 024 [arXiv:0806.4495] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  46. М. Дрессельхаус, Г. Дрессельхаус и А. Джорио, Теория групп: приложение к физике конденсированного состояния , SpringerLink, Springer, Германия (2007).

  47. М. Деринг, Х. В. Хаммер, М. Май, Дж. Ю. Панг, t. А. Русецкий и Дж. Ву, Трехчастичный спектр в конечном объеме: роль кубической симметрии , Физ. Ред. D 97 (2018) 114508 [arXiv:1802.03362] [INSPIRE].

  48. Коллаборация Hadron Spectrum, Эффективное решение многоканального детерминанта Люшера посредством разложения по собственным значениям , Физ. Ред. D 101 (2020) 114505 [arXiv:2001.08474] [INSPIRE].

  49. Э. Эпельбаум, Х.-В. Хаммер и У.-Г. Meissner, Современная теория ядерных сил , Rev. Mod. физ. 81 (2009) 1773 [arXiv:0811.1338] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  50. Р. Махлейдт и Д. Р. Энтем, Киральная эффективная теория поля и ядерные силы , Физ. Представитель 503 (2011) 1 [arXiv:1105.2919] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  51. Э. Эпельбаум, Х. Кребс и П. Райнерт, Высокоточные ядерные силы от хирального EFT: современное состояние, проблемы и перспективы , Фронт. в физ. 8 (2020) 98 [arXiv:1911.11875] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  52. E. Epelbaum, H. Krebs and U.G. Meißner, Прецизионный нуклон-нуклонный потенциал пятого порядка в киральном расширении , Phys. Преподобный Летт. 115 (2015) 122301 [arXiv:1412.4623] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  53. P. Reinert, H. Krebs and E. Epelbaum, Полулокальные импульсные регуляризованные киральные двухнуклонные потенциалы до пятого порядка , Евро. физ. J. A 54 (2018) 86 [arXiv:1711.08821] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  54. Д. Р. Энтем, Р. Махлейдт, Ю. Носик, Высококачественные двухнуклонные потенциалы до пятого порядка кирального расширения , Физ. Ред. C 96 (2017) 024004 [arXiv:1703.05454] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  55. Э. Эпельбаум, В. Глокль и У.-Г. Meissner, Улучшение сходимости кирального расширения для ядерных сил. 2. Низкие фазы и дейтрон , Eur. физ. J. A 19 (2004) 401 [nucl-th/0308010] [INSPIRE].

  56. В. Бару, К. Ханхарт, М. Хоферихтер, Б. Кубис, А. Ногга и Д. Р. Филлипс, Прецизионный расчет порога π − и ГМО правило сумм , Нукл. физ. A 872 (2011) 69 [arXiv:1107.5509] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  57. P. Reinert, H. Krebs and E. Epelbaum, Прецизионное определение констант пион-нуклонного взаимодействия с использованием теории эффективного поля , Phys. Преподобный Летт. 126 (2021) 092501 [arXiv:2006. 15360] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  58. Э. Эпельбаум, В. Глокль и У.-Г. Meissner, Улучшение сходимости кирального расширения для ядерных сил. 1. Периферийные фазы , Eur. физ. J. A 19 (2004) 125 [nucl-th/0304037] [INSPIRE].

  59. В. Г. Дж. Стокс, Р. А. М. Кломп, М. К. М. Рентмистер и Дж. Дж. де Сварт, Парциально-волновой анализ всех данных нуклон-нуклонного рассеяния ниже 350 МэВ , Phys. Ред. C 48 (1993) 792 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  60. М. Май, М. Деринг, К. Калвер и А. Александру, Трехчастичная унитарность против конечного объема π + π + π 900 62 + спектр от решетки КХД , Физ. Ред. D 101 (2020) 054510 [arXiv:1909. 05749] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  61. I. Fachruddin, C. Elster and W. Gloeckle, Нуклон-нуклонное рассеяние в трехмерном приближении , Nucl. физ. A 689 (2001) 507 [nucl-th/0104027] [INSPIRE].

  62. В. Г. Дж. Стокс и Дж. Дж. Де Сварт, Взаимодействие магнитных моментов в анализе нуклон-нуклонного фазового сдвига , Phys. C 42 (1990) 1235 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  63. Дж. Дж. Дудек, Р. Г. Эдвардс и К. Э. Томас, Фазовые сдвиги S- и D-волн в рассеянии пи-пи изоспина-2 в КХД на решетке , Phys. Ред. D 86 (2012) 034031 [arXiv:1203.6041] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  64. Коллаборация Hadron Spectrum, DK I = 0 , \( D\overline{K}I \) = 0 , 1 рассеяние и \( {D}_{s0}^{ \аст } \) (2317) из решетки QCD , JHEP 02 (2021) 100 [arXiv:2008. 06432] [INSPIRE].

  65. В. Бару, Э. Эпельбаум, А. А. Филин и Дж. Гегелия, Низкоэнергетические теоремы для нуклон-нуклонного рассеяния при нефизических массах пионов , Phys. Ред. C 92 (2015) 014001 [arXiv:1504.07852] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  66. В. Бару, Э. Эпельбаум и А. А. Филин, Низкоэнергетические теоремы для нуклон-нуклонного рассеяния на M π = 450 МэВ , Физ. Ред. C 94 (2016) 014001 [arXiv:1604.02551] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  67. В. Бернар, Н. Кайзер и У. Г. Мейснер, Киральная теория возмущений при наличии резонансов: приложение к пи-пи и пи-К-рассеянию , Nucl. физ. Б 364 (1991) 283 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  68. П. К. Брунс и У.-Г. Meissner, Инфракрасная регуляризация для полей со спином 1 , Eur. физ. J. C 40 (2005) 97 [hep-ph/0411223] [INSPIRE].

  69. Р. М. Волошин, А. Д. Джексон, Сравнение трехмерных релятивистских уравнений рассеяния , Nucl. физ. Б 64 (1973) 269 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  70. Л. Кастильехо, Р. Х. Далиц и Ф. Дж. Дайсон, Уравнение рассеяния Лоу для заряженных и нейтральных скалярных теорий , Phys. 101 (1956) 453 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  71. Дж. А. Оллер, Э. Осет и Дж. Э. Паломар, Форм-факторы векторов пиона и каона , Phys. Ред. D 63 (2001) 114009 [hep-ph/0011096] [INSPIRE].

  72. Дж. Гассер и Х. Лейтвайлер, Киральная теория возмущений: расширения в массе странного кварка , Nucl. физ. B 250 (1985) 465 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  73. Г. Эккер, Дж. Гассер, А. Пич и Э. де Рафаэль, Роль резонансов в киральной теории возмущений , Nucl. физ. B 321 (1989) 311 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  74. Extended Twisted Mass, коллаборация ETM, ρ-резонанс от N f = 2 КХД на решетке, включая физическую массу пиона , Phys. лат. B 819 (2021) 136449 [arXiv:2006.13805] [INSPIRE].

  75. П. Эстабрукс и А. Д. Мартин, Анализ фазового сдвига ππ ниже порога \(K\overline{K} \) , Nucl. физ. B 79 (1974) 301 [ВДОХНОВЕНИЕ].

  76. S. D. Protopopescu et al., ππчастичный волновой анализ по реакциям π + p → π + π 900 22 − ∆ ++ и π + р → К + К − ∆ ++ в 7 . 1 ГэВ/c , Физ. Ред. D 7 (1973) 1279 [INSPIRE].

  77. Сотрудничество ETM, Хранилище данных , https://github.com/urbach/datarhonf2.

  78. Ф. Джеймс, Минимизация функций MINUIT и анализ ошибок: справочное руководство, версия 94.1 , CERN-D-506 (1994).

  79. Филин А.А., Бару В., Эпельбаум Э., Кребс Х., Меллер Д. и Райнерт П., Извлечение радиуса заряда нейтрона из точного расчета радиуса структуры дейтрона , Phys. Преподобный Летт. 124 (2020) 082501 [arXiv:1911.04877] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  80. Филин А.А., Меллер Д., Бару В., Эпельбаум Э., Кребс Х. и Райнерт П., Высокоточный расчет заряда дейтрона и квадрупольных формфакторов в киральной теории эффективного поля , Физ. Ред. C 103 (2021) 024313 [arXiv:2009.08911] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  81. Коллаборация NPLQCD, Дейтрон и экзотические двухчастичные связанные состояния из решеточной КХД , Phys. Ред. D 85 (2012) 054511 [arXiv:1109.2889] [INSPIRE].

  82. Коллаборация HAL КХД, Двухбарионные потенциалы и H-дибарион из моделирования КХД на решетке с тремя ароматами , Нукл. физ. A 881 (2012) 28 [arXiv:1112.5926] [INSPIRE].

  83. Т. Ямадзаки, К.-и. Исикава, Ю. Курамаси и А. Укава, Ядра гелия, дейтрон и динейтрон в 2 + 1 решетке аромата КХД , Физ. Ред. D 86 (2012) 074514 [arXiv:1207.4277] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  84. Т. Ямадзаки, К.-и. Исикава, Ю. Курамаси и А. Укава, 9 лет0091 Исследование зависимости энергии связи легких ядер от массы кварка в решетке аромата 2 + 1 КХД , Phys. Ред. D 92 (2015) 014501 [arXiv:1502.04182] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  85. К. Оргинос, А. Паррено, М. Дж. Сэвидж, С. Р. Бин, Э. Чанг и В. Детмольд, Две нуклонные системы на m π ∼ 900 62 450 МэВ из решеточной КХД 9{\mathrm{phys}} \) : Первый расчет КХД на решетке со стохастическим лапласианским методом Хевисайда , Phys. Ред. C 103 (2021) 014003 [arXiv:2009.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *