Мысленный эксперимент галилея: Недопустимое название | Мысленные Эксперименты Wiki

Содержание

Эксперименты Галилея по падению тел

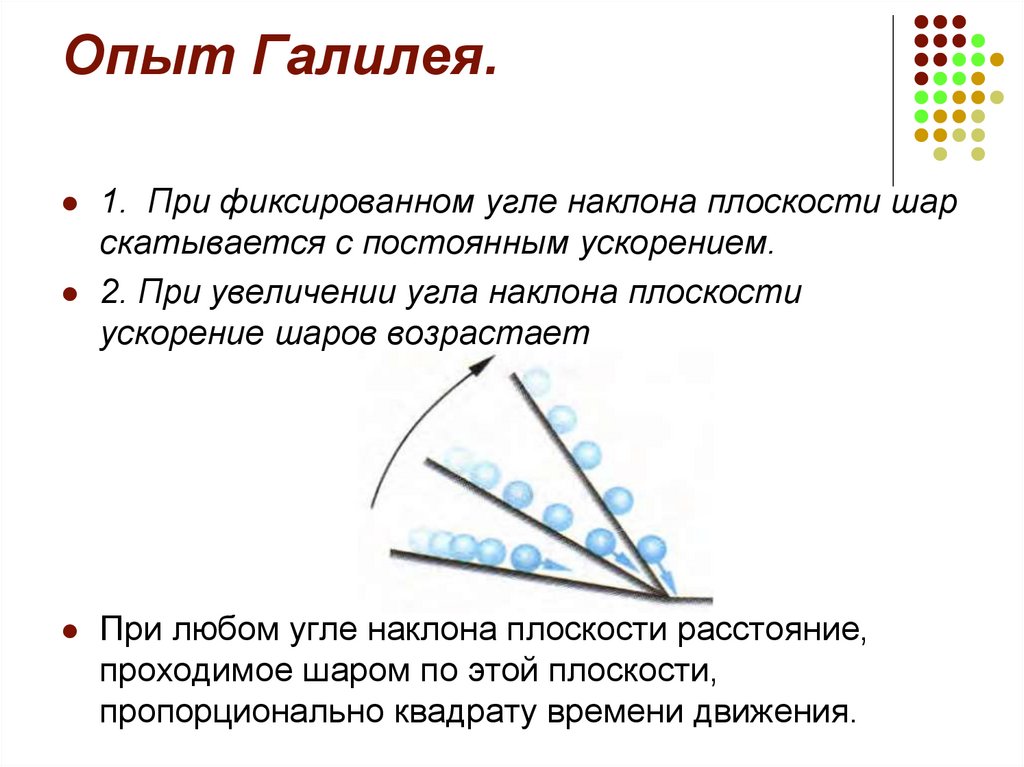
02.12.2020

Согласно биографии Галилео Галилея, написанной его учеником Винченцо Вивиани, в 1589 году Галилей провёл эксперимент, сбросив два шара различной массы со знаменитой падающей башни в Пизе, чтобы продемонстрировать, что время падения не зависит от массы шара. С помощью этого эксперимента Галилей якобы обнаружил, что тела упали практически одновременно, опровергнув теорию Аристотеля, которая утверждала, что скорость падения пропорциональна массе тела. В то время, когда, по описанию Вивиани, Галилей проводил свой эксперимент, он ещё не сформулировал окончательный вариант своего закона свободного падения.

Хотя история об экспериментах Галилея на Пизанской башне вошла в научный фольклор, в трудах самого Галилея нет упоминания об этих экспериментах, и большинство историков науки склонны считать, что это был лишь мысленный эксперимент, который на самом деле не осуществлялся. Исключение составляет лишь позиция Дрейка, который считает, что эксперимент Галилея имел место в действительности примерно в том виде, как это описал Вивиани.

Опыты по падению тел

Одним из первых опровергнуть утверждение Аристотеля попытался нидерландский учёный Симон Стевин. Можно предположить, что его результаты были известны Галилею.

Галилей так описывает знаменитый мысленный эксперимент в своей книге «О движении».

Представьте себе два предмета, один из которых тяжелее другого, соединённых верёвкой друг с другом, и сбросьте эту связку с башни. Если мы предположим, что тяжёлые предметы действительно падают быстрее, чем лёгкие и наоборот, то лёгкий предмет должен будет замедлять падение тяжёлого. Но поскольку рассматриваемая система в целом тяжелее, чем один тяжёлый предмет, то она должна падать быстрее него. Таким образом мы приходим к противоречию, из которого следует, что изначальное предположение (тяжёлые предметы падают быстрее лёгких) — неверно.

Опыты с качением тел по наклонной плоскости

Из-за несовершенства измерительного оборудования того времени свободное падение тел изучать было почти невозможно. В поисках способа уменьшения скорости движения Галилей заменил свободное падение на качение по наклонной поверхности, где были значительно меньшие скорости и сопротивление воздуха. Было замечено, что со временем скорость движения растет — тела движутся с ускорением. Был сделан вывод, что скорость и ускорение не зависят ни от массы, ни от материала шара.

Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая:

Все тела при падении движутся одинаково: начав падать одновременно, они движутся с одинаковой скоростью.

Движение происходит с постоянным ускорением.

Ученый также отметил: если соединить две наклонные поверхности так, чтобы скатившись по одной из них, шар поднимался по другой, он поднимется на ту же высоту, с которой начал движение, независимо от наклона каждой из поверхностей.

Галилей проверил, что полученные им законы скатывания качественно не зависят от угла наклона плоскости, и, следовательно, их можно распространить на случай падения. Окончательный вывод Галилея из последней его книги: скорость падения нарастает пропорционально времени, а путь — пропорционально квадрату времени.

Блэр (замок)
Чемпионат Италии по кёрлингу среди женщин 2017
XVI Галльский легион
Суворов, Алексей Динарович
Кучерово (Красноярский край)
Де Лука, Ник
Доказательства геноцида армян
1956 год в спорте
Приеде, Анна Августовна
Спутники Марса

мысленный эксперимент: mi3ch — LiveJournal

: Дмитрий Чернышев (mi3ch) wrote,
2019-08-12 23:34:00

Categories:

История
Философия
getCancelledCats().length > 0″ ng-click=»catSuggester.reacceptAll()»> Cancel

Аристотель утверждал, казалось бы, очевидное – тяжелые тела падают быстрее, чем легкие. Его опроверг Галилей. Нам неизвестно, на самом ли деле Галилей бросал два шара – легкий и тяжелый с Пизанской башни. Но известно, что он опроверг Аристотеля логически.

В своей книге «О движении» Галилей писал:

Представьте себе два предмета, один из которых тяжелее другого, соединённых верёвкой друг с другом, и сбросьте эту связку с башни. Если мы предположим, что тяжёлые предметы действительно падают быстрее, чем лёгкие и наоборот, то лёгкий предмет должен будет замедлять падение тяжёлого.

Но поскольку рассматриваемая система в целом тяжелее, чем один тяжёлый предмет, то она должна падать быстрее него. Таким образом мы приходим к противоречию, из которого следует, что изначальное предположение (тяжёлые предметы падают быстрее лёгких) — неверно.

Tags: history

деньги
На войне всегда не хватает всего. И главный вопрос руководства — на что именно потратить доступные стране ресурсы? Если мы посмотрим на военный…
рифмы
Мексиканская революция. 1917 год. Капитан Фортино Самано докуривает сигарету и с презрительной улыбкой смотрит в лицо солдатам. Через несколько…
китайская ферма
Марк Солонин делает сейчас очень интересный разбор Войны Судного дня. Он подробно рассказывает, почему Израиль понес тяжелейшие потери в той…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

← Ctrl ← Alt

Next
Ctrl → Alt →

деньги
На войне всегда не хватает всего. И главный вопрос руководства — на что именно потратить доступные стране ресурсы? Если мы посмотрим на военный…
рифмы
Мексиканская революция. 1917 год. Капитан Фортино Самано докуривает сигарету и с презрительной улыбкой смотрит в лицо солдатам. Через несколько…
китайская ферма
Марк Солонин делает сейчас очень интересный разбор Войны Судного дня. Он подробно рассказывает, почему Израиль понес тяжелейшие потери в той…

№ 166: Эксперимент Галилея

№ 166:
ЭКСПЕРИМЕНТ ГАЛИЛЕЯ
Джон Х. Х. Линхард

Щелкните здесь для прослушивания аудио эпизода 166.

Сегодня мы спрашиваем, как быстро все рушится, и переписываем наука. Колледж Университета Хьюстона Engineering представляет серию о машинах которые заставляют нашу цивилизацию работать, а людей чья изобретательность создала их.

Когда Галилей был молод, один его современники использовали эти слова для описания Идея Аристотеля о том, как предметы падают:
Для всего есть естественное место, как:
Тяжелые предметы идут вниз, Огонь вверх,
И реки к морю.
Это было в природе падения, сказал Аристотель, что тяжелые предметы быстрее ищут свое естественное место чем легкие — тяжелые предметы падают быстрее.
Галилей интересовался темпами падения, когда было около 26 лет, и он был учителем математики в Университет Пизы.
Ему казалось, что — с нет сопротивления воздуха — тело должно падать со скоростью пропорциональна его плотности. Он решил испытать этот модифицированный аристотелевский взгляд, сделав эксперимент.
Не было традиции описания экспериментальных исследования во времена Галилея. Контролируемые эксперименты были почти неизвестны. Так что отчет Галилея был хорош скудный. Кажется, он бросил разные мячи с башни. Но какие веса? Какая башня? Мы можем быть уверенным, что это была Пизанская башня. Но в конечном итоге мы сомневаемся, действительно ли он это сделал. эксперимент. Может быть, он просто сообщил, что он мысль должна была произойти.

Один результат эксперимента удивил Галилея. один нас удивляет. Галилей обнаружил, что тяжелый шар упал на землю первым, но только немного. За исключением небольшой разницы, вызванной воздухом сопротивление, оба шара достигли почти одинакового скорость. И это его удивило. Это заставило его отказаться от аристотелевских представлений о движении. Если он действительно провел эксперимент, это был, безусловно, поворот точку в истории науки.
Но что нас удивляет, так это то, что, по словам Галилея, произошло сразу после того, как он выпустил два шара. Он говорит более легкий мяч всегда стартовал немного быстрее чем тяжелый мяч. Затем настиг тяжелый мяч. Это звучит безумно.

Итак, Томас Сеттл и Дональд Миклич перезапустили Эксперимент Галилея с башней перед камерой. Ан помощник держал четырехдюймовые железные и деревянные шары в на расстоянии вытянутой руки — как Галилей должен был бы держаться их, чтобы очистить широкую балюстрату на вершине Пизы башня. Оказывается, когда вы пытаетесь их сбросить оба сразу, ваши напряженные мышцы обманывают вас. Ты последовательно отпускайте более легкую, ту, во-первых, вы сжимали менее интенсивно. Что означает, что Галилей точно сообщил, что он видел происходящее. И у нас не осталось сомнений что он действительно провел эксперимент.

Галилео стал первым настоящим претендентом Аристотеля. Его эксперимент с башней не был сказкой. ни одно яблоко не упало на голову Ньютона. Это был один из первые контролируемые научные эксперименты. Нравиться большинство сегодняшних экспериментов было несовершенным. Но этот эксперимент изменил Галилея, и он изменил история.
Я Джон Линхард из Хьюстонского университета, где нас интересует, как изобретательные умы работа.
(Музыкальная тема)

Settle, T.B., Galileo and Early Experimenting, Источники научного творчества
, (Ф. Арис, Х.Т. Дэвис и Р. Х. Стювер, ред.). Миннеаполис: Университет. Миннесота Пресс, 1983, стр. 3-20.
Подробнее об эксперименте с башней см. отличная веб-страница Galileo: http://es.rice.edu/ES/humsoc/Galileo/Things/on_motion.html.

Фото Джона Линхарда
Двигатели нашей изобретательности Copyright © 1988-2018 Джон Х. Линхард.
Предыдущий Эпизод | Поиск эпизодов | Индекс | Дом | Далее Эпизод

Ускорительный эксперимент Галилея

предыдущий индекс следующие

Майкл Фаулер, Факультет физики UVa

Обобщение взглядов Аристотеля

Аристотель считал, что существует два вида движения неживой материи: естественные и неестественные. Неестественное (или «жестокое») движение — это когда что-то толкается, и в этом случае скорость движения пропорциональна к силе толчка. (Это, вероятно, было выведено из наблюдения за повозками с волами и лодки.) Естественное движение — это когда что-то ищет свое естественное место в Вселенной, например, падающий камень или поднимающийся огонь. (Мы говорим только здесь о веществах, состоящих из земли, воды, воздуха и огня, «природных круговое движение» планет, состоящее из обеих, считается в отдельности).

Для естественного движения тяжелых предметов, падающих на землю, Аристотель утверждал что скорость падения была пропорциональна весу , а обратно пропорционально пропорциональна плотности среды , через которую проваливается тело. Он также упомянул, что было некоторое ускорение, так как тело приближалось больше приблизился к своей стихии, его вес увеличился, и он ускорился. Однако эти замечания у Аристотеля очень кратки и расплывчаты и, конечно, не количественны.

На самом деле, эти взгляды Аристотеля не остались без внимания даже в древних Афинах. Примерно через тридцать лет после смерти Аристотеля Стратон указал, что камень падение с большей высоты оказало большее воздействие на землю, что предполагает что камень набирал большую скорость, когда падал с большей высоты.

Две новые науки

Галилей изложил свои идеи о падающих телах и о снарядах в вообще, в книге под названием « Две новые науки ».

Эти двое были наука о движении, ставшая краеугольным камнем физики, и наука о материалах и конструкции, важный вклад в инженерное дело.

Идеи представлены в живой форме в виде диалога с участием трех персонажи, Сальвиати, Сагредо и Симпличио. Официальная церковная точка зрения, то есть аристотелизм, выдвигается персонажем по имени Симпличио, и обычно сносят другие. Защита Галилея при обвинении в ересь в подобной книге заключалась в том, что он просто излагал все точки зрения, но это несколько неискренне — Симплицио почти всегда изображается как простодушный.

Например, на странице 62 TNS Сальвиати указывает:

Я очень сомневаюсь, что Аристотель когда-либо проверял экспериментально, верно, что два камня, один из которых в десять раз тяжелее другого, если допустить упасть в одно и то же мгновение с высоты, скажем, 100 локтей, было бы так отличаются по скорости, что, когда более тяжелый достиг земли, другой не упали более чем на 10 локтей.

Симпличио отвечает на это не думать с точки зрения выполнения испытать себя, чтобы ответить на вызов Сальвиати, но тщательно изучить ближе священное писание:

SIMP: Судя по его языку, он пробовал поэкспериментируйте, потому что он говорит: мы видим тяжелее ; теперь слово см. показывает, что он провел эксперимент.

Затем присоединяется Сагредо:

САГР: Но я, Симпличио, который сделал тест, могу заверить вас, что пушечное ядро весом в сто-двести фунтов, а то и больше не долетит землю на целых пяди впереди мушкетной пули весом всего в половину фунта, при условии, что оба они будут сброшены с высоты 200 локтей.

Это знаменует собой начало современной эры в науке — отношение что утверждения о физическом мире со стороны авторитетов, какими бы мудрыми или почитается, стоять или падать экспериментальным испытанием. Легенда гласит, что Галилей провел этот конкретный эксперимент с падающей башни в Пизе.

Галилей продолжает подробный анализ падающих тел. Он понимает что для очень легких предметов, таких как перья, сопротивление воздуха становится доминирующий эффект, тогда как в эксперименте он имеет лишь незначительное значение изложено выше.

Естественно ускоренное движение

Экспериментально установив, что тяжелые предметы падают практически С той же скоростью Галилей продолжил рассмотрение центрального вопроса о скорости падения едва затронутый Аристотелем — как изменяется скорость при падении?

Проблема в том, что очень сложно ответить на этот вопрос просто смотреть, как что-то падает — все кончается слишком быстро. Чтобы сделать любой вид измерения скорости движение должно быть каким-то образом замедлено. Конечно, некоторые падающие движения естественно медленные, например, перо или что-то другое слишком тяжелое падение через воду. Наблюдая за этими движениями, можно увидеть, что после при падении тело быстро набирает определенную скорость, а затем равномерно падает с эта скорость. Ошибка, которую совершали люди, состояла в том, что они полагали, что все падающие тела следовали той же схеме, так что большая часть падения происходила с постоянной скоростью. скорость. Галилей утверждал, что эта точка зрения ложна, повторяя забытые слова Стратона почти две тысячи лет назад:

(ТНС, стр. 163) Но скажите мне, господа, не правда ли, что если блок будет позволено упасть на кол с высоты четырех локтей и вбить его в земли, скажем, в четыре пальца ширины, что, исходящее с высоты двух локтей, загонит кол на гораздо меньшее расстояние; и, наконец, если блок будет поднят всего на один палец, насколько больше он сделает, чем если просто наложить вершина кола без перкуссии? Конечно очень мало. Если его поднять только толщина листа, эффект будет совершенно незаметен. И поскольку эффект удара зависит от скорости этого ударяющего тела, может ли кто-нибудь сомневаться в том, что движение очень медленное … всякий раз, когда эффект незаметно?

Гипотеза ускорения Галилея

Установив с помощью приведенных выше аргументов и экспериментов, что тело продолжает набирать скорость или ускоряться по мере падения, предположил Галилей простейшая возможная гипотеза (перефразируя обсуждение на странице 161 TNS):

Падающее тело равномерно ускоряется: оно набирает равные скорости через равные промежутки времени, так что если он падает из состояния покоя, то движется в два раза быстрее быстро через две секунды, так как он двигался через одну секунду, и двигался через три раза быстрее через три секунды, чем через одну секунду.

Это привлекательная простая гипотеза, но Галилею не так-то просто ее обосновать. проверить опытным путем — как он мог дважды измерить скорость падающего камня осенью и сделать сравнение?

Замедление движения

Хитрость заключается в том, чтобы замедлить движение каким-то образом, чтобы скорость могла быть измерено, без изменения в то же время характера движения .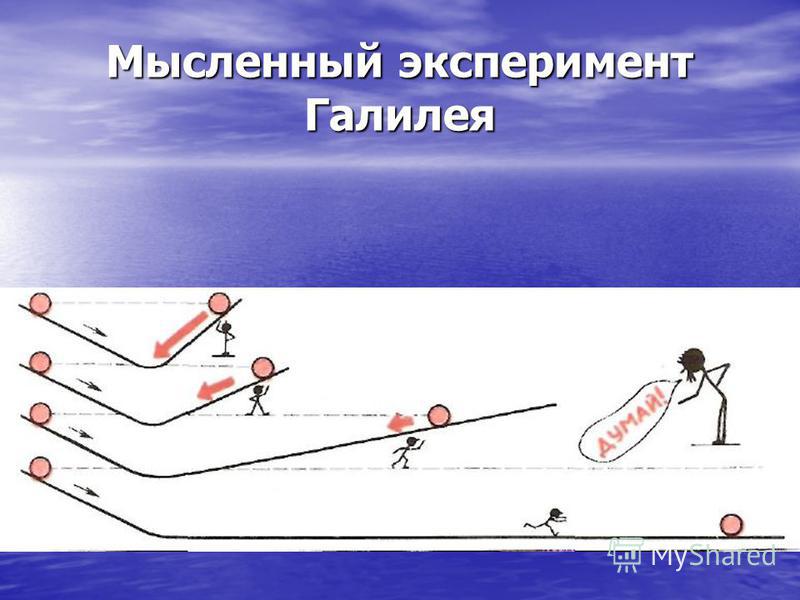 Галилей знал, что падение в воду чего-либо, падающего довольно мягко, сделал изменить характер движения, он приземлился бы так же мягко на дно упал с десяти футов так же, как и с двух футов, поэтому замедлил движение падение чего-то через воду полностью изменило ситуацию.

Идея Галилея для замедления движения заключалась в том, чтобы катить мяч вниз по пандусу, а не падать вертикально. Он утверждал, что скорость, набранная в скатывание по пандусу заданной высоты не зависело от уклона. Его аргумент был основан на эксперименте с маятником и гвоздем, показанном на стр. 171 из Две новые науки . Маятник состоит из нити и поводка пуля. Его отводят в сторону, а нить натянута до некоторой точки C.

Гвоздь помещается в точке E непосредственно под верхним концом нити, так что маятник качается в своей нижней точке, нить попадает в гвоздь и маятник эффектно укорочен, благодаря чему пуля более круто качается вверх, к G с гвоздем в E. Тем не менее маятник будет качаться назад до почти такой же высоты он начался, то есть точки G и C находятся на одной высоте над уровнем земли. Кроме того, когда он откидывается назад, он снова поднимается до точки С, если пренебречь небольшой потерей воздуха сопротивление. Отсюда можно сделать вывод, что скорость, с которой мяч проходит через самую низкую точку одинакова в обоих направлениях. Чтобы увидеть это, представьте сначала ситуация без гвоздя в E. Мяч будет качаться назад и вперед симметричным образом, обычный маятник, и конечно в этом случае скорость в нижней точке одинакова для обоих направлениях (опять же игнорируя постепенное замедление от сопротивления воздуха). Когда мы вбить гвоздь, однако, мы видим из эксперимента, что на качели назад, мяч все же успевает попасть в начальную точку C. Делаем вывод, что он должно быть, двигался с той же скоростью, с которой он качнулся назад через самую низкую точку как тогда, когда гвоздя не было, потому что в тот момент, когда он оставляет гвоздь на обратный ход это всего лишь обычный маятник, и как далеко он раскачивается от вертикали зависит от того, как быстро он движется в самой нижней точке.

Галилей утверждает, что аналогичная картина будет наблюдаться, если мяч скатится вниз пандус, который плавно соединяется с другим более крутым пандусом, т. мяч скатится по второй рампе до уровня, практически равного уровню, на котором он начал в, даже если две рампы имеют разные наклоны. Тогда это будет продолжайте катиться назад и вперед между двумя пандусами, в конце концов останавливается из-за трения, сопротивления воздуха и т. д.

Если подумать об этом движении, становится ясно, что (без учета вниз при последовательных проходах) он должен идти та же скорость отрывается одна рампа, как она отрывается от другой. Затем Галилей предлагает представить себе вторая рампа все круче и круче — и мы видим, что если она достаточно крутая, мы можем думать о мяче как о простом падении! Он заключает, что на мяч скатываясь по пандусу, скорость на различных высотах одинакова со скоростью мяч достиг бы (гораздо быстрее!), просто упав вертикально с его начальная точка на этой высоте . Но если мы сделаем пандус достаточно пологим, движение будет достаточно медленным для измерения. (на самом деле разница есть между катящимся мячом и плавно скользящим или падающим мячом, но не влияют на характер увеличения скорости, поэтому мы не будем здесь останавливаться на этом.)

Эксперимент Галилея по ускорению

Теперь мы готовы рассмотреть эксперимент Галилея, в котором он испытал его гипотеза о том, как падающие тела набирают скорость. Мы цитируем счет из «Двух новых наук», стр. 178:

Кусок деревянного бруса длиной около 12 локтей, была взята ширина в локоть и толщина в три пальца; по его краю была вырезана канал шириной чуть больше одного пальца; сделав этот паз очень прямой, гладкой и полированной, и выстлав ее пергаментом, также как гладкой и отполированной, мы катили по ней твердую, гладкую и очень круглый бронзовый шар. Разместив эту доску в наклонном положении, подняв один конец на один-два локтя выше другого, мы катали мяч, как я просто говорю вдоль канала, отмечая способом, который сейчас будет описан, время, необходимое для спуска. Мы повторили этот эксперимент более один раз, чтобы измерить время с такой точностью, чтобы отклонение между двумя наблюдениями никогда не превышала одной десятой доли пульса. Имея выполнили эту операцию и убедившись в ее надежности, мы теперь катил мяч только четверть длина канала; и измерив время его спуска, мы нашли ровно половину бывшего. Далее пробовали другие дистанции, сравнивали время на весь длина с той, что на половину, или с той, что на две трети, или на три четверти, или действительно для любой дроби; в таких опытах, повторенных сто раз, мы всегда находили, что пройденных пространств относились друг к другу как квадраты времени , и это было справедливо для всех наклонов плоскости, т. е. канал, по которому мы катили мяч. Мы также заметили, что времена спуск, при различных наклонах самолета, относились друг к другу точно то соотношение, которое, как мы увидим позже, автор предсказал и продемонстрировано для них.

Для измерения времени мы использовали большой сосуд с водой, помещенный в возвышенном положении; ко дну этого сосуда была припаяна трубка из небольшой диаметр, дающий тонкую струю воды, которую мы собрали в небольшой стакан во время каждого спуска, будь то по всей длине канала или на часть своей длины; собранную таким образом воду взвешивали после каждого спуск, на очень точном равновесии; различия и соотношения этих веса дали нам различия и соотношения времен, и это при таком точность в том, что хотя операция повторялась много-много раз, нет заметных расхождений в результатах.