Обобщение это в философии: Обобщение (философия) | это… Что такое Обобщение (философия)?

Обобщение (философия) | это… Что такое Обобщение (философия)?

Толкование

Обобщение (философия)

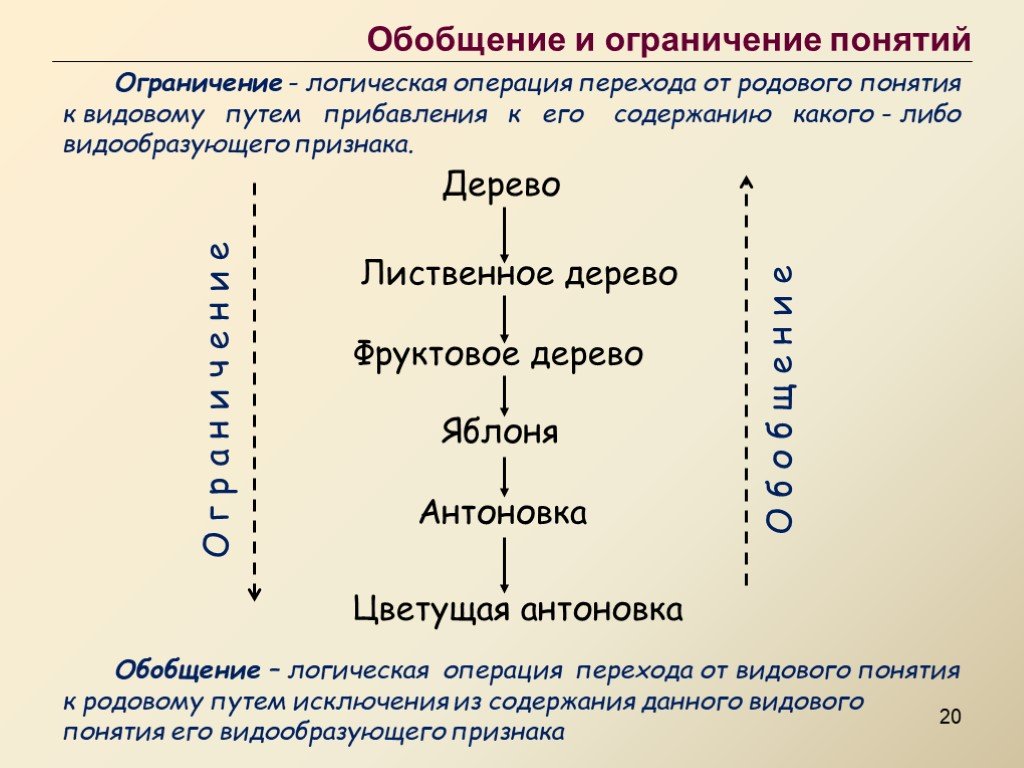
Обобщение понятий — логическая операция, посредством которой в результате исключения видового признака получается понятие более широкого объема. Например, «доверенность» — «документ» — «деловая бумага».

Обобщение, форма приращения знания путём мысленного перехода от частного к общему в некоторой модели мира, что обычно соответствует и переход на более высокую ступень абстракции. «Мысленное выделение каких-нибудь свойств, принадлежащих некоторому классу предметов, и формулирование такого вывода, который распространяется на каждый отдельный предмет данного класса.»^[1]

Пример: переход от наблюдения над совокупностями индивидуализированных объектов к мысленному их разбиению на классы равночисленных совокупностей и далее к понятию натурального числа.

Содержание 1 Проблема научно-теоретического обобщения 2 Обобщение как задача искусственного интеллекта 3 Ссылки 4 Литература 5 Смотри также

Проблема научно-теоретического обобщения

Проблема научно-теоретического обобщения состоит в следующем. Отличается ли научно-теоретическое обобщение (понятие), претендующее на всеобщность и необходимость, от любого эмпирически-индуктивного «обобщения»?

Сложности, здесь возникающие, остроумно обрисовал Б. Рассел в виде забавной притчи:

живет в курятнике курица, каждый день приходит хозяин, приносит ей зернышек поклевать, курица, несомненно, сделает отсюда вывод: появление хозяина связано с появлением зернышек. Но в один прекрасный день хозяин явится в курятник не с зернышками, а с ножом, чем убедительно и докажет курице, что ей не мешало бы иметь более тонкое представление о путях научного обобщения.

.. .

Обобщение как задача искусственного интеллекта

Формулирование задачи было сделано Ф. Розенблаттом.

В эксперименте по «чистому обобщению» от модели мозга или перцептрона требуется перейти от избирательной реакции на один стимул (допустим, квадрат, находящийся в левой части сетчатки) к подобному ему стимулу, который не активизирует ни одного из тех же сенсорных окончаний (квадрат в правой части сетчатки). К обобщению более слабого вида относится, например, требование, чтобы реакции системы распространялись на элементы класса подобных стимулов, которые не обязательно отделены от уже показанного ранее (или услышанного, или воспринятого на ощупь) стимула.

Так же как и в случае экспериментов по различению, и в этом случае можно исследовать спонтанное обобщение, при котором критерии подобия не вводятся извне или не навязываются экспериментатором, и принудительное обобщение

, при котором экспериментатор с помощью соответствующей процедуры «обучает» систему понятию подобия.

Ссылки

1. ↑ Кондаков Н.И. Логический словарь-справочник, Изд. 2, М.:Наука, 1975, с. 395, «Обобщение».

Литература

• Коротаев А. В., Малков А. С., Халтурина Д. А. Законы истории. Математическое моделирование развития Мир-Системы. Демография, экономика, культура. 2-е изд. М.: УРСС, 2007.
• Коротаев А. В., Комарова Н. Л., Халтурина Д. А. Законы истории. Вековые циклы и тысячелетние тренды. Демография, экономика, войны. 2-е изд. М.: УРСС, 2007.
• Ильенков Э.В. Диалектическая логика. Очерки истории и теории. 2‑е изд., доп. М.: Политиздат, 1984. – 320 с.
• Мате Э., Тиксье Д. Логистика. С-Петербург: Дом «Нева», 2003. 120 с.

Смотри также

• Аксиома выбора
• Абстрагирование
• Асимметрия
• Индуктивное умозаключение
• Онтология
• Информационный работник
• Информационная экономика
• DIKW

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

• Обобщенная схема размещения
• Обобщенная функция Жуковского

Полезное

Обобщение (философия) | это… Что такое Обобщение (философия)?

Толкование

Обобщение (философия)

Обобщение понятий — логическая операция, посредством которой в результате исключения видового признака получается понятие более широкого объема. Например, «доверенность» — «документ» — «деловая бумага».

Обобщение, форма приращения знания путём мысленного перехода от частного к общему в некоторой модели мира, что обычно соответствует и переход на более высокую ступень абстракции. «Мысленное выделение каких-нибудь свойств, принадлежащих некоторому классу предметов, и формулирование такого вывода, который распространяется на каждый отдельный предмет данного класса.

«^[1]

Пример: переход от наблюдения над совокупностями индивидуализированных объектов к мысленному их разбиению на классы равночисленных совокупностей и далее к понятию натурального числа.

Содержание 1 Проблема научно-теоретического обобщения 2 Обобщение как задача искусственного интеллекта 3 Ссылки 4 Литература 5 Смотри также

Проблема научно-теоретического обобщения

Проблема научно-теоретического обобщения состоит в следующем. Отличается ли научно-теоретическое обобщение (понятие), претендующее на всеобщность и необходимость, от любого эмпирически-индуктивного «обобщения»?

Сложности, здесь возникающие, остроумно обрисовал Б. Рассел в виде забавной притчи:

живет в курятнике курица, каждый день приходит хозяин, приносит ей зернышек поклевать, курица, несомненно, сделает отсюда вывод: появление хозяина связано с появлением зернышек. Но в один прекрасный день хозяин явится в курятник не с зернышками, а с ножом, чем убедительно и докажет курице, что ей не мешало бы иметь более тонкое представление о путях научного обобщения… .

Обобщение как задача искусственного интеллекта

Формулирование задачи было сделано Ф. Розенблаттом.

В эксперименте по «чистому обобщению» от модели мозга или перцептрона требуется перейти от избирательной реакции на один стимул (допустим, квадрат, находящийся в левой части сетчатки) к подобному ему стимулу, который не активизирует ни одного из тех же сенсорных окончаний (квадрат в правой части сетчатки). К обобщению более слабого вида относится, например, требование, чтобы реакции системы распространялись на элементы класса подобных стимулов, которые не обязательно отделены от уже показанного ранее (или услышанного, или воспринятого на ощупь) стимула.

Так же как и в случае экспериментов по различению, и в этом случае можно исследовать спонтанное обобщение, при котором критерии подобия не вводятся извне или не навязываются экспериментатором, и принудительное обобщение, при котором экспериментатор с помощью соответствующей процедуры «обучает» систему понятию подобия.

Ссылки

1. ↑ Кондаков Н.И. Логический словарь-справочник, Изд. 2, М.:Наука, 1975, с. 395, «Обобщение».

Литература

• Коротаев А. В., Малков А. С., Халтурина Д. А. Законы истории. Математическое моделирование развития Мир-Системы. Демография, экономика, культура. 2-е изд. М.: УРСС, 2007.
• Коротаев А. В., Комарова Н. Л., Халтурина Д. А. Законы истории. Вековые циклы и тысячелетние тренды. Демография, экономика, войны. 2-е изд. М.: УРСС, 2007.
• Ильенков Э.В. Диалектическая логика. Очерки истории и теории. 2‑е изд., доп. М.: Политиздат, 1984. – 320 с.
• Мате Э., Тиксье Д. Логистика. С-Петербург: Дом «Нева», 2003. 120 с.

Смотри также

• Аксиома выбора
• Абстрагирование
• Асимметрия
• Индуктивное умозаключение
• Онтология
• Информационный работник
• Информационная экономика
• DIKW

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

• Обобщенная схема размещения
• Обобщенная функция Жуковского

Полезное

правил как обобщения | Игра по правилам: философское исследование принятия решений на основе правил в законе и в жизни

Фильтр поиска панели навигации Oxford AcademicИгра по правилам: философское исследование принятия решений на основе правил в праве и в жизниЮриспруденция и философия праваОксфордская стипендия OnlineBooksJournals Мобильный Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicИгра по правилам: философское исследование принятия решений на основе правил в праве и в жизниЮриспруденция и философия праваОксфордская стипендия OnlineBooksJournals Введите поисковый запрос

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения
• Делиться
  • Фейсбук
  • Твиттер
  • LinkedIn
  • Электронная почта

Укажите

ШАУЭР, ФРЕДЕРИК, «Правила как обобщения», Игра по правилам: философское исследование принятия решений на основе правил в законе и в жизни , Clarendon Law Series (

Oxford , 1993; онлайн-издание, Oxford Academic, 22 март 2012 г. ), https://doi.org/10.1093/acprof:oso/9780198258315.003.0002, по состоянию на 28 мая 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicИгра по правилам: философское исследование принятия решений на основе правил в праве и в жизниЮриспруденция и философия праваОксфордская стипендия OnlineBooksJournals Мобильный Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicИгра по правилам: философское исследование принятия решений на основе правил в праве и в жизниЮриспруденция и философия праваОксфордская стипендия OnlineBooksJournals Введите поисковый запрос

Advanced Search

Abstract

В этой главе исследуется взаимосвязь между правилами и описательными обобщениями в контексте принятия решений. Полученные данные раскрывают потенциал описательного обобщения для сосредоточения внимания на нерелевантном и подавления релевантного, а поскольку предписывающие правила включают в себя описательные обобщения, они также содержат те характеристики, которые приводят к ошибкам. В этой главе делается вывод о том, что предписывающие правила могут быть либо потенциально, либо фактически неполными или чрезмерными.

Ключевые слова: описательные обобщения, предписывающие правила, ошибки

Предмет

Юриспруденция и философия права

Коллекция: Оксфордская стипендия онлайн

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Щелкните Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные учетные записи Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные учетные записи Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов учреждения

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Логика

.

Почему универсальное обобщение должно работать для абстрактных объектов?

спросил 1 год, 5 месяцев назад

Изменено 11 месяцев назад

Просмотрено 284 раза

В свободное время я читаю книгу по логике, и обычно правило вывода универсального обобщения мотивируется примерами из реальной жизни. утром как кофе. Тогда можно доказать, что все с каштановыми волосами любят кофе: пусть x обозначает человека с каштановыми волосами, тогда x устал по утрам и, следовательно, x любит кофе. Поскольку мы ничего не предполагали об объекте (в данном случае о человеке) x, кажется разумным, что для каждого объекта (человека) x рассуждение должно быть верным. Если бы это было не так, то это означало бы, что должен существовать объект y, который не удовлетворяет этому свойству, но тогда мы могли бы просто провести такое же доказательство для этого самого y.

Теперь, когда я перехожу к абстрактным объектам (например, к натуральным числам для простоты), мне это сложнее. Я подозреваю, что это связано с абстракцией математических объектов (какими они должны быть?). При доказательстве чего-либо обо всех натуральных числах снова принято обозначать n любой объект, который удовлетворяет требованиям быть элементом натуральных чисел, а затем выводить утверждение. Поскольку мы принимаем правило вывода универсального обобщения, это верно для всех натуральных чисел.

Вопрос: Однако почему разумно предположить, что универсальное обобщение справедливо для натуральных чисел (или, в более общем случае, для абстрактных объектов)? Есть ли хорошие точки зрения на этот счет? Я предполагаю, что «очевидный» — это просто следовать примеру из реальной жизни, но мне любопытно, есть ли какие-либо другие взгляды на это, поскольку я, кажется, немного борюсь с поиском лучших.

• логика
• философия математики
• философия логики
• универсальные

7

Вот еще один взгляд на этот вопрос. Пусть a,b,c… относятся к типу «люди с каштановыми волосами». Пусть x,y,z…. имеют тип «натуральное число». Давайте возьмем ваш пример с кофе:

Допустим, у вас есть некоторая алгоритмическая процедура, с помощью которой вы можете получить доказательство того, что любой x, то есть любое натуральное число, обладает некоторым свойством P; кроме того, такая процедура не опирается ни на какое конкретное свойство х, кроме того факта, что х имеет естественный тип. Это похоже на ваше утверждение о том, что любой человек с каштановыми волосами любит кофе — оно не зависит ни от каких фактов о конкретном человеке, а только от его «каштановых волос».

Поскольку предполагаемое доказательство опирается только на свойство быть натуральным, а не на какое-либо конкретное свойство какого-либо конкретного натурального числа, оно может быть продублировано для любого натурального числа. Следовательно, у вас есть доказательство того, что каждый натуральный имеет P.

Ситуация полностью аналогична приведенному выше примеру с кофе, за исключением того, что здесь наличие каштановых волос означает наличие свойства быть натуральным числом.

Под «универсальным обобщением», я полагаю, вы подразумеваете правило, что если вы можете вывести P(x), то вы можете вывести и x.P(x). Есть два способа понять это. Во-первых, вы можете рассматривать его как формальное свойство логики. Если логика позволяет вам вводить и рассуждать со свободными переменными, то ей нужно правило, чтобы сказать, что означает предложение со свободной переменной. Правило не должно иметь никакого значения помимо этого. Например, в некоторых исчислениях есть правило переименования, которое в основном говорит, что вы можете изменить имя переменной, если вы делаете это определенным образом. Это чисто формально и не имеет высшего значения.

Универсальное обобщение приводит к неявной универсальной количественной оценке всех несвязанных переменных. Без универсального обобщения было бы неясно, что означает P(x), когда x — несвязанная переменная (то есть, когда x не константа и не связана квантором. В этом смысле правило — это просто формальное свойство логики.