Корреляция, корреляционная зависимость
Корреляция (от лат. correlatio), корреляционная зависимость — взаимозависимость двух или нескольких случайных величин. Суть ее заключается в том, что при изменении значения одной переменной происходит закономерное изменение (уменьшению или увеличению) другой(-их) переменной(-ых).
При расчете корреляций пытаются определить, существует ли статистически достоверная связь между двумя или несколькими переменными в одной или нескольких выборках. Например, взаимосвязь между ростом и весом детей, взаимосвязь между успеваемостью и результатами выполнения теста IQ, между стажем работы и производительностью труда.
Важно понимать, что корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях. Например, если бы исследуемой выборке между ростом и весом человека существовала корреляционная зависимость то, это не значило бы, что вес является причиной роста человека, иначе сбрасывая лишние килограммы рост человека также уменьшался. Корреляционная связь лишь говорит о взаимосвязанности данных параметров, причем в данной конкретной выборке, в другой выборке мы можем не наблюдать полученные корреляции.
Показатель корреляции. Коэффициент корреляции (r) характеризует величину отражающую степень взаимосвязи двух переменных между собой. Он может варьировать в пределах от -1 (отрицательная корреляция) до +1 (положительная корреляция). Если коэффициент корреляции равен 0 то, это говорит об отсутствии корреляционных связей между переменными. Причем если коэффициент корреляции ближе к 1 (или -1) то говориться о сильной корреляции, а если ближе к 0, то о слабой.
При положительной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному увеличению (или уменьшению) другой переменной т.е. взаимосвязи типа увеличение-увеличение (уменьшение-уменьшение).
При отрицательной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному уменьшению (или увеличению) другой переменной т.е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).
Корреляция (синонимы): соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие.
statpsy.ru
Взаимосвязь между временем, посвященным занятиям, и оценками
Взаимосвязь между временем, посвященным занятиям, и оценками является примером положительной корреляции. Приведенные ниже данные, полученные в ходе гипотетического исследования восьми студентов, говорят о наличии положительной корреляции. В данном случае первой переменной является время, операционально определенное как количество часов в неделю, потраченных на учебу, а второй — средний балл (СБ), варьирующийся от 0,0 до 4,0.
| Время, потраченное на учебу | СБ | |
| Студент 1 | 42 | 3,3 |
| Студент 2 | 23 | 2,9 |
| Студент 3 | 31 | 3,2 |
| Студент 4 | 35 | 3,2 |
| Студент 5 | 16 | 1,9 |
| Студент 6 | 26 | 2,4 |
| Студент 7 | 39 | 3,7 |
| Студент 8 | 19 | 2,5 |
Значительное время, потраченное на учебу (42 часа), связано с высоким средним баллом (3,3), а самое малое время (16 часов) — с низким баллом (1,9).
Примером отрицательной корреляции может быть взаимосвязь между бесполезно потраченным временем и средним баллом. Бесполезно потраченное время можно операционально определить как количество часов в неделю, потраченное на определенные занятия, например на игру в видеоигры, просмотр телесериалов или игру в гольф (конечно, эти виды деятельности можно назвать и «терапией»). Ниже приведены гипотетические данные для других восьми студентов. На этот раз вы увидите обратную взаимосвязь между количеством часов в неделю, потраченных впустую, и средним баллом:
| Время, потраченное па учебу | СБ | |
| Студент 1 | 42 | 1,8 |
| Студент 2 | 23 | 3,0 |
| Студент 3 | 31 | 2,2 |
| Студент 4 | 35 | 2,9 |
| Студент 5 | 16 | 3,7 |
| Студент 6 | 26 | 3,0 |
| Студент 7 | 39 | 2,4 |
| Студент 8 | 19 | 3,4 |
Обратите внимание, что при отрицательной корреляции переменные имеют обратную взаимосвязь: большое количество потраченного зря времени (42) связано с низким средним баллом (1,8), а небольшое (16) — с более высоким (3,7).
Силу корреляции показывает особая величина описательной статистики, носящая название «коэффициент корреляции».
Коэффициент корреляции равен -1,00 в случае прямой отрицательной корреляции, 0,00 при отсутствии взаимосвязи и + 1,00 при полной положительной корреляции. Наиболее распространенным коэффициентом корреляции является пирсоново г (о нем упоминалось во вставке 9.1), названное так в честь британского ученого, соперничающего в известности с сэром Рональдом Фишером. Пирсоново г вычисляется для данных, полученных с помощью интервальной шкалы или шкалы отношений. В случае других шкал измерений рассматриваются другие виды корреляции. К примеру, для порядковых данных (т. е. упорядоченных) вычисляется «ро» Спирмена. В приложении С показано, как вычислять пирсоново r.
Так же как среднее арифметическое и стандартное отклонение, коэффициент корреляции является величиной описательной статистики. В ходе заключительного анализа определяется, является ли конкретная корреляция значимо большей (или меньшей) нуля. Таким образом, для корреляционных исследований нулевая гипотеза (Н0) говорит, что действительное значение r равно 0 (т. е. нет никаких взаимосвязей), а альтернативная гипотеза (Н) — что r № 0. Отвергнуть нулевую гипотезу — значит решить, что между двумя переменными существует значимая взаимосвязь. В приложении С показано, как определить, является ли корреляция статистически значимой.
psihologia.biz
Отрицательная корреляция 2019
Поделиться видео // www. Investopedia. ком / условия / п / отрицательная корреляция. aspЧто такое «Отрицательная корреляция»
Отрицательная корреляция — это взаимосвязь между двумя переменными, в которых одна переменная увеличивается по мере уменьшения другой, и наоборот. В статистике абсолютная отрицательная корреляция представлена значением -1. 00, а значение 0. 00 означает отсутствие корреляции и +1. 00 указывает на идеальную положительную корреляцию. Совершенная отрицательная корреляция означает, что соотношение между двумя переменными отрицательно в 100% случаев.
BREAKING DOWN «Отрицательная корреляция»
Отрицательная корреляция используется в статистике для измерения суммы, которую изменение одной переменной может повлиять на противоположное изменение в другой переменной. Для количественной оценки предсказуемости отрицательной взаимосвязи между двумя переменными аналитики проводят регрессионный анализ. Эта процедура предоставляет аналитикам расчет R-квадрата (R2), который является статистическим показателем того, насколько хорошо одна переменная предсказывает значение другой переменной. Если R2 между двумя отдельными элементами равно 1, это означает, что независимая переменная точно прогнозирует зависимую переменную без ошибок. R2 из 0 означает, что независимая переменная не может предсказать зависимую переменную. R2, который находится между 0 и 1, измеряет степень, в которой независимая переменная предсказывает зависимую переменную. Например, если R2 равно 0. 4, это означает, что независимая переменная может предсказать зависимую переменную с точностью 40%.
Например, чем больше времени человек проводит в торговом центре, покупая товары, тем меньше денег у него на его текущем счете. Чем выше коэффициент взаимных инвестиций инвестора, тем ниже его доходность инвестиций. Чем больше часов человек проводит в офисе, тем меньше времени у него на другие занятия. Все эти переменные имеют отрицательный R2.
Почему важна отрицательная корреляция
Отрицательная корреляция важна для любого аналитика, инвестора или человека, который хочет диверсифицировать и хеджировать свои ставки. Если инвестор сможет найти инвестиционный класс, который движется напротив другого набора активов, который он держит, он может инвестировать в оба, чтобы стабилизиро
ru.toptipfinance.com
ОТРИЦАТЕЛЬНАЯ КОРРЕЛЯЦИЯ — это… Что такое ОТРИЦАТЕЛЬНАЯ КОРРЕЛЯЦИЯ?
- ОТРИЦАТЕЛЬНАЯ КОРРЕЛЯЦИЯ
вид корреляционной зависимости между случайными величинами, при к-рой условные средние значения одной из них уменьшаются при возрастании значений другой величины. Об О. к. между величинами с
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- ОТРИЦАТЕЛЬНАЯ ВАРИАЦИЯ ФУНКЦИИ
- ОТРИЦАТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Смотреть что такое «ОТРИЦАТЕЛЬНАЯ КОРРЕЛЯЦИЯ» в других словарях:
отрицательная корреляция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN antithetical correlationnegative correlation … Справочник технического переводчика
отрицательная корреляция — neigiamoji koreliacija statusas T sritis fizika atitikmenys: angl. inverse correlation; negative correlation vok. negative Korrelation, f rus. отрицательная корреляция, f pranc. corrélation négative, f … Fizikos terminų žodynas
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Корреляция — Корреляция (корреляционная зависимость) статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или… … Википедия
КОРРЕЛЯЦИЯ — (CORRELATION) При проведении социологического исследования обычно одновременно получают множество разнообразных данных: например, при проведении обследований могут измеряться достижения в образовании и профессиональный уровень респондентов. Если… … Социологический словарь
Корреляция и регрессия (correlation and regression) — Рассмотрение К. и Р. строится вокруг следующих осн. вопросов: а) существует ли между переменными X и Y такого рода связь, что по известным нам значениям X мы могли бы, по крайней мере с разумной степенью точности, предсказать значения Y? б)… … Психологическая энциклопедия
КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ — англ. correlation, negative; нем. Korrelation, negative. Корреляция, при к рой увеличение одной переменной связано с уменьшением другой переменной. В этом случае коэффициент корреляции имеет отрицательные значения в пределах от 0 до 1. Antinazi.… … Энциклопедия социологии
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
КОРРЕЛЯЦИЯ ОБРАТНАЯ — см. КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
dic.academic.ru
КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ — это… Что такое КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ?
- КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ
-
— англ. correlation, negative; нем.
Antinazi. Энциклопедия социологии, 2009
- КОРРЕЛЯЦИЯ ОБРАТНАЯ
- КОРРЕЛЯЦИЯ ПОЛОЖИТЕЛЬНАЯ
Смотреть что такое «КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ» в других словарях:
Корреляция отрицательная — корреляция, при которой увеличение значения одной переменной определённым образом связано с уменьшением значения другой (коэффициент корреляции имеет отрицательное значение, расположенное между 0 и 1) … Энциклопедический словарь по психологии и педагогике
КОРРЕЛЯЦИЯ, ОТРИЦАТЕЛЬНАЯ — Корреляция, при которой увеличение одной переенной связано с уменьшением другой или при которой высокие значения одной переменной связаны с низкими значениями другой. Коэффициент будет иметь отрицательные значения между 0 и 1,00. Также называется … Толковый словарь по психологии
КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ — англ. correlation, negative; нем. Korrelation, negative. Корреляция, при к рой увеличение одной переменной связано с уменьшением другой переменной. В этом случае коэффициент корреляции имеет отрицательные значения в пределах от 0 до 1 … Толковый словарь по социологии
КОРРЕЛЯЦИЯ ОБРАТНАЯ — см. КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
КОРРЕЛЯЦИЯ ОБРАТНАЯ — См. КОРРЕЛЯЦИЯ ОТРИЦАТЕЛЬНАЯ … Толковый словарь по социологии
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
отрицательная корреляция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN antithetical correlationnegative correlation … Справочник технического переводчика
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
Корреляция — Корреляция (корреляционная зависимость) статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или… … Википедия
dic.academic.ru
Корреляция полная отрицательная — Энциклопедия по экономике
Коэффициент корреляции может изменяться в диапазоне 1,0. Коэффициент +1,0 (полная положительная корреляция) означает, что изменения независимой переменной приведут к идентичным изменениям зависимой (т.е. изменение индикатора вызовет такое же изменение цены бумаги). Коэффициент 1,0 (полная отрицательная корреляция) означает, что изменения независимой переменной вызовут идентичные изменения зависимой, но в противоположном направлении. Коэффициент, равный нулю, свидетельствует об отсутствии связи между переменными, то есть изменения независимой переменной не влияют на изменения зависимой. [c.104]Коэффициент корреляции всегда лежит в интервале между -1 и +1. Если он равен — 1, то это означает полную отрицательную корреляцию, если +1 — полную положительную корреляцию. В большинстве случаев он находится между этими двумя экстремальными значениями. [c.182]
Коэффициент корреляции — зто статистическая мера степени корреляции между двумя рядами показателей. Изменяется от -1 в случае полной отрицательной корреляции до +1 в случае полной положительной корреляции. [c.811]
Из гл. 2 мы знаем, что коэффициент корреляции может принимать значения от + 1 (полная положительная корреляция) до —1 (полная отрицательная корреляция). Положительная корреляция означает, что доходности каждой пары активов в основном изменяются в одном направлении. Это соотношение тем сильнее, чем ближе коэффициент корреляции к + 1. Отрицательная корреляция показывает, что доходности изменяются в противоположных направлениях, при этом соотношение становится сильнее по мере того, как коэффициент приближается к — 1. [c.187]
При полной отрицательной корреляции доходов динамика квадратического отклонения доходов от портфеля более сложная. По мере движения от точки Л к точке К эта величина сначала сокращается и доходит до нуля в точке В, затем растет (см. рис. 8.4). Следует обратить внимание на то, что при движении от Л1 до В рост дохода сопровождается уменьшением риска (квадратического отклонения). [c.175]
При полной отрицательной корреляции находим [c.179]
Для интерпретации коэффициента корреляции необходимо знать область его существования 0 коэффициента корреляции может быть достигнуто, если положительные и отрицательные произведения отклонений признаков от их средних величин в числителе полностью уравновесят друг друга. Это свидетельствовало бы о полном отсутствии связи, но вероятность такого абсолютно точного взаимопогашения крайне мала для любой реальной, не бесконечно большой совокупности. Поэтому и при отсутствии реальной связи коэффициент корреляции на практике не равен нулю. Например, коэффициент корреляции между надоем молока от коров и числом букв в названии предприятия в совокупности хозяйств, указанных в табл. 8.1, равен +0,216. Как отделить реальные, надежно установленные связи от таких случайных, незначимых величин коэффициента корреляции, рассматривается в следующем разделе этой главы. [c.246]
Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения [c.241]
Коэффициент корреляции доходности по двум финансовым инструментам инвестирования может принимать значения от +1 (означающего полную и положительную корреляцию между рассматриваемыми величинами) до -1 (означающего полную и отрицательную корреляцию между рассматриваемыми величинами). Используя различия в ковариации инвестиционного дохода, можно подобрать в формируемый портфель такие виды финансовых инструментов, которые, не меняя уровня средней доходности портфеля, позволяют существенно снизить уровень его риска. [c.389]
Коэффициент корреляции может принимать любые значения от 0 до 1. Если коэффициент корреляции равен нулю, то это означает отсутствие связи между х и у. Если его абсолютная величина составляет единицу, то, следовательно, существует полная зависимость между исследуемыми факторами, т, е, корреляционная зависимость совпадает с функциональной. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между х и у чем ближе к нулю, тем связь слабее. Положительное значение коэффициента корреляции указывает на прямую зависимость, отрицательное значение — обратную. [c.115]
К = -I, т. с. четвертое свойство коэффициентов ранговой корреляции. Это означает, что ранжированные показатели по признакам X и Y полностью противоположны, разнонаправленны. В таком случае аудитор может утверждать, что один ранжированный ряд (например, исчисленный по фактическим показателям функционирования данной хозяйственной системы в конкретном квартале) полностью «переставлен», инвертирован по отношению к другому, эталонному. Из всех возможных режимов функционирования, моделируемых и контролируемых при помощи данного набора п показателей, этот — единственный абсолютно отрицательный. Он означает не только замедление, но практически полное торможение развития системы, ее деградацию, отсутствие какого бы то ни было, даже медленного продвижения от предыдущего состояния к другому, более высокому состоянию. [c.127]
Если доходы по обоим видам ценных бумаг явно коррелируют (т. е. положительный эффект по одному виду всегда сопровождается положительным эффектом по другому виду, а отрицательный эффект — всегда отрицательным), это означает полную корреляцию с коэффициентом корреляции +1. Аналогичным образом возможна противоположная ситуация, когда положительному эффекту по одному виду всегда соответствует отрицательный эффект по другому виду ценных бумаг, и наоборот. В этом случае коэффициент корреляции между двумя видами равен — 1. [c.158]
Наше исследование коэффициента корреляции предполагает, что для полного устранения риска предприятие должно вкладывать средства в проекты, доходы от которых совершенно отрицательно коррелированны. Если это так, изменчивость доходов от различных проектов взаимно сокращается, и поэтому риск полностью устраняется. Однако, к сожалению, возможность следовать подобной инвестиционной политике встречается редко. В реальном мире крайне сложно [c.224]
Этот коэффициент может принимать значения от минус единицы до плюс единицы. Коэффициент, равный минус единице, указывает на полную отрицательную корреляцию, коэффициент, равный плюс единице, — на полную положительную корреляцию, коэффициент, равный нулю,— на отсутствие связи. Заключенные между этими крайними величинами значения указывают на степень взаимосвязи. Обратите внимание на то, что коэффициент отражает степень только линейной взаимосвязи переменных. Например, две переменные могут быть тесно связаны нелинейным соотношением (скажем, у =х2), а значение г будет невысоким. (См. также rank orrelation.) [c.102]
Определим доход и дисперсию для портфеля с долями, равными, допустим, 0,3 и 0,7. Получим по формулам (8.6) и (8.7) D = 0,651 + 0,37лху и А — 2,7. Таким образом, при полной положительной корреляции D = 1,021, при полной отрицательной корреляции О = 0,281. В итоге с вероятностью 95% можно утверждать, что суммарный доход находится в первом случае в преде- [c.176]
Плотность ковариации между уровнями доходности по двум видам финансовых инструментов можно определить, рассчитав коэффициент корреляции, который может принимать значения от +1 до —1. Значение коэффициента корреляции, равное +1, означает полную и положительную корреляцию между уровнями доходности изучаемых финансовых инструментов, т. е. однонаправленное совпадающее изменение. Значение, равное —1, показывает полную и отрицательную корреляцию между уровнями доходности рассматриваемых финансовых инструментов. Следовательно, когда доходность одной ценной бумаги наиболее высока, велика вероятность того, что доходность второй ценной бумаги принимает наиболее низкие значения. Расчет коэффициента корреляции осуществляется по следующей формуле [c.392]
Что произойдет, если добавлять в портфель все большее количество новых акций Как правило, риск портфеля будет уменьшаться по мере увеличения числа акций Если дополнить портфель достаточно большим количеством акций, можно ли полностью свести риск к нулю В целом ответ на этот вопрос отри цательный, однако степень воздействия добавления новых акций на снижение риска портфеля зависит от уровня корреляции между отдельными акциями чем меньше значение коэффициента корреляции, тем ниже риск крупного портфеля. На самом деле если бы в распоряжении инвестора имелось достаточно акций с коэффициентом корреляции, равным нулю (или отрицательным), риск можно было бы полностью элиминировать. Однако в большинстве случаев коэффици енты корреляции между отдельными акциями положительны, но не достигают +1.0, поэтому можно лишь снизить риск портфеля, но не устранить его полно стью [c.58]
Некоторая (не слишком существенная) часть из сочетаний Коткл и КИНБ> приведенных в табл. 6.10, и особенно те из сочетаний, в которых исчислено значение KPA3B при положительных и отрицательных значениях исходных коэффициентов ранговой корреляции (такие случаи редки), на практике может оказаться бессодержательной. Но без их значений данная таблица не давала бы полной системной картины математической зависимости между различными значениями этих коэффициентов, а потому она приведена именно в этом виде. [c.148]
Мы провели собственное исследование ротации секторов и обнаружили, что есть негативная корреляция между результатами последовательных лет, по крайней мере для не- которых из секторов рынка. В период с 1987 по 1998 год индекс Nasdaq после года, в котором наблюдалось падение на 10%, в среднем вырастал на 25%. В 2000-2001 годах произошла практически полная смена лучших и худших секторов, входящих в индекс S P 500. Два лучших и два худших сектора по итогам 2000 года в 2001 году поменялись местами, и корреляция рейтингов между двумя годами оказалась высокой и отрицательной -0,8. Это соответствует предположению о том, что для покупки акций существует лишь ограниченный запас энергии (первый закон термодинамики), и одновременно второму закону термодинамики — закону энтропии, который постулирует, что потенциальная энергия спонтанно стремится высвободиться. [c.427]
economy-ru.info
Понятие корреляционной связи — Мегаобучалка
Термин «корреляция» (от латинского correlatio – соотношение, взаимосвязь) применяется в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия, соотношения понятий, предметов, функций.
Широкое распространение в науке термин «корреляция» получил благодаря работам английского ученого-естествоиспытателя Френсиса Гальтона (1822-1911 гг.). В 1888 году Ф. Гальтон сформулировал свои представления о корреляции в работе «Корреляция и ее измерение». Продолжил научную работу в области корреляции британский ученый Карл Пирсон (1857-1936 гг.). Идеи Пирсона о корреляции были опубликованы в серии из 18 книг (между 1893 и 1912 гг.) под заголовком «Математический вклад в теорию эволюции». Также результатом его работы явился широко известный коэффициент корреляции Пирсона.
Корреляционная связь — это согласованные изменения двух признаков или большего количества признаков (множественная корреляционная связь). Корреляционная связь отражает тот факт, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого.
О силе и направленности корреляционной связи мы можем судить по значению коэффициента корреляции.
Коэффициент корреляции — статистический показатель степени (силы) и направленности взаимосвязи между двумя переменными.
Коэффициент корреляции мы можем определить с помощью корреляционного анализа.
Корреляционным анализом называется совокупность методов обнаружения корреляционной связи между случайными величинами или признаками. Корреляционный анализ — это проверка гипотез о связях между переменными.
Задача корреляционного анализа сводится к установлению направления (положительного или отрицательного) и формы связи (линейной, криволинейной) между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Необходимо отметить, что согласованные изменения признаков и отражающая это корреляционная связь между ними может свидетельствовать не о зависимости этих признаков между собой, а о зависимости обоих этих признаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании. Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков, или она оказывается за пределами исследуемой пары признаков — установить этот факт с помощь корреляционного анализа невозможно. Найти причину изменений мы можем с помощью дополнительных исследований и обработки данных, например, с помощью дисперсионного анализа.
Корреляционные связи различаются по форме, направлению и степени (силе).
По формекорреляционные связи могут быть прямолинейными или криволинейными. В свою очередь прямолинейная корреляционная связь может различаться по направлению и быть прямой (положительной) или отрицательной (обратной) (см. рис. 9.1).
Рис. 9.1 Схема прямолинейных корреляционных связей: а) положительная (прямая) корреляционная связь; б) отрицательная (обратная) корреляционная связь
В случае прямой или положительной корреляции взаимосвязь характеризуется тем, что высокие значения одной переменной связаны с высокими значения другой, а также низкие значения первой переменной – с низким значениями второй. Графически такая связь представляется прямой линией, отсюда ее более короткое название – линейная связь.
В качестве примера можно привести взаимосвязь роста человека и его веса, т.е. чем выше человек тем, как правило, он больше весит, и наоборот чем меньше рост, тем меньше вес.
Отрицательная корреляция означает обратную взаимосвязь. Высокие значения одной переменной связаны с низкими значениями другой, и наоборот. Например, у людей с высокой тревожностью, как правило, низкая самооценка.
О том, с каким направлением корреляции (положительной или отрицательной) мы имеем дело, можно судить по знаку коэффициента корреляции. При положительной корреляции коэффициент корреляции имеет положительный знак, например r = +0,87, при отрицательной корреляции — отрицательный знак, например r = – 0,87.
При криволинейных связях с возрастанием значения одного признака возрастание (или убывание) другого признака происходит неравномерно, или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, параболой и т.д.).
Например, криволинейной может быть связь между уровнем возбуждения и результативностью выполнения задания. Сложные задания выполняются хорошо при среднем уровне возбуждения, но гораздо хуже при очень низком или очень высоком (см. например, Anderson, 1990). При очень низком уровне возбуждения у человека недостаточно сил, чтобы работать над заданием, а очень высокое возбуждение мешает эффективной обработке информации, требующейся для выполнения работы (см. рис. 9.2).
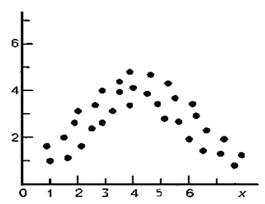
Рис. 9.2 Криволинейная корреляционная связь
Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное возможное абсолютное значение коэффициента корреляции r = +1,00 или r = –1,00; минимальное r = 0. Если коэффициент корреляции по модулю оказывается близким к +1,00 или – 1,00 то это соответствует высокому уровню связи между переменными, а близким к нулю — низкому уровню связи.
Величина коэффициента линейной корреляции не может превышать + 1 и быть меньше чем – 1. Эти два числа +1 и – 1 являются границами для коэффициента корреляции. Когда при расчете получается величина большая + 1 или меньшая – 1 то, это свидетельствует о том, что произошла ошибка в вычислениях.
megaobuchalka.ru