Положение об испытательном сроке образец
]]>Подборка наиболее важных документов по запросу Положение об испытательном сроке образец (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).
Формы документов: Положение об испытательном сроке образецСтатьи, комментарии, ответы на вопросы: Положение об испытательном сроке образец Открыть документ в вашей системе КонсультантПлюс:Статья: Альтернативное трудоустройство при прекращении трудового договора: обязанности работодателя
(Зорина О.О.)
(«Трудовое право в России и за рубежом», 2019, N 2)Стоит отметить, что за рубежом можно найти примеры закрепления на законодательном уровне положения о необходимости установления испытательного срока (trial period) при предложении работодателем альтернативной работы. Так, в Великобритании предусмотрен испытательный срок (4 недели) в целях оценки работодателем и работником, подходит ли последнему предложенная работа.
«По делу о проверке конституционности положений Уголовного кодекса Российской Федерации, регламентирующих правовые последствия судимости лица, неоднократности и рецидива преступлений, а также пунктов 1 — 8 Постановления Государственной Думы от 26 мая 2000 года «Об объявлении амнистии в связи с 55-летием Победы в Великой Отечественной войне 1941 — 1945 годов» в связи с запросом Останкинского межмуниципального (районного) суда города Москвы и жалобами ряда граждан»Попытки предложить определение природы судимости настолько противоречивы и несовместимы друг с другом, что не вызывают доверия.
Не справился с этим и законодатель, предложив в статье 86 УК Российской Федерации лишь классический пример тавтологии: лицо, осужденное … считается судимым. В советской правовой доктрине под судимостью понимали то особое правовое состояние или положение осужденного, то личные качества или свойства преступления, то репрессивные или ограничительные меры, то отягчающие и квалифицирующие обстоятельства преступления, то отрицательные морально-политические качества и характеристики личности как общественно опасной, то средство закрепления целей наказания, его продолжение, испытательный срок, превентивную меру и т.д.Важные тавтологии в науке. Часть 1. Физика / Хабр
Вы знаете, что такое логическая тавтология? Наверное знаете. А на тот случай, если вы этого не знаете, автор постарается сейчас объяснить это понятие. Не станем переходить на сухой и формальный язык математики, не будем бездушными педантами, как Википедия, и скажем образно: тавтология это подобие Уробороса, кусающего свой собственный хвост.
Императору Сарлака Гранту Сциентикусу III было скучно. Очень скучно. Обычно, когда он чувствовал скуку, он играл в камни (
довольно простая, но хитрая игра, похожая одновременно на наши шашки, реверси и Го). Однако сегодня никто из философов, обычно игравших с ним, не пришёл. Он сидел понурившись, и разглядывал одну из позиций.
Внутренний экспериментатор Гранта решил сосчитать число возможных позиций. Давайте покинем его на этом месте, и займемся своим собственным подсчетом.
По правилам разрешается иметь до 3 камней на одной клетке.
Всего камней 6 (по 3 у каждого игрока). Мы не станем считать число всех возможных позиций. Куда как интереснее посчитать, сколькими способами можно выложить позицию. Но, для начала, посмотрите на рисунок.
Для простоты мы пока рассматриваем лишь одну клетку. Указанную выше позицию можно получить, например, вот такими тремя способами, отличающимися тем, какие именно камни мы выкладывали на доску:
  
Мы условно раскрасили камни, чтобы можно было отличить их друг от друга. Очевидно, способов намного больше трёх. Но сколько именно? Первый из трёх камней мы можем выбрать шестью способами. Каждый из этих шести вариантов продолжается выбором второго камня из оставшихся пяти, и последнего из оставшихся четырех. Имеем , однако при этом мы допустили повторы, например, красный-синий-желтый, желтый-красный-синий и синий-красный-желтый это одна и та же «выкладка».
Чтобы найти число повторов, найдём сколькими способами мы можем выложить на доску три камня одного цвета.
Первым может быть любой из трех нужных камней, вторым должен быть один из оставшихся двух, третьим обязательно будет последний нужный нам камень: .
В итоге, имеем 120/6=20 способов выложить камни требуемым образом. Давайте назовем это число весом данной позиции. Ничего общего с физическим весом оно, конечно же, не имеет, просто это название является общепринятым в статистике.
Усложним задачу. Давайте посчитаем веса вот этих позиций:
  
Если вам лень разбираться во всей этой математике, пропустите следующий абзац.
Первая позиция:
- Выкладываем 2 камня на одну из двух левых клеток:
- На вторую клетку выкладываем два камня из оставшихся 4:
- Итого имеем способов.
Для второй и третьей имеем соответственно
и
. Деление во всех случаях выполняется для того, чтобы избавиться от повторов.
Итак, имеем следующие веса: 90 для первой раскладки, 180 для второй и 360 для третьей.
Вы заметили, что чем более упорядочена позиция, тем меньше её вес? Его величество Грант это заметил. И теперь он собирается посчитать вес для реальных игровых позиций.
  
У него получается, соответственно 90, 360 и 720. Однако тут его терпение кончается (как, наверное, и ваше). Он расстроенно толкает доску, беспорядочно разметав камни и замечает стоящего у дверей философа Клофзюса.
— А скажи-ка мне, философ, — спрашивает он с нотками недовольства, — почему, когда я толкаю доску, камни разлетаются по ней беспорядочно, равномерно, а не укладываются с краю по три в клетке?
Клофзюс, в ответ на это улыбнулся и сказал:
— Я некоторое время наблюдал за вашими подсчётами, повелитель, и вы, наверно могли бы уже и сами ответить на этот вопрос. Но я всё же скажу — упорядочиться с края доски камни могут девяносто разными способами, а рассеяться по всем клеткам — семьсот двадцатью. Для камней существует намного больше способов быть разбросанными по доске равномерно, чем собранными с краю.
Пожалуй, тут мы покинем Сарлак. Но обратите внимание на объяснение Клофзюса: камни рассыпаются по доске потому, что для них существуют куда больше способов быть рассыпанными равномерно, чем быть разложенными полностью упорядоченно. И разница между количествами способов (весами раскладок камней) тем больше, чем больше доска и число камней. Для доски в 15 клеток (3 на 5) и 15 камней вес полностью упорядоченной раскладки (по 3 камня в клетке вдоль одного края) равен примерно 1.4 миллионам (1401400 если точно) а для равномерной (по одному в каждой клетке) — примерно 1.3 квадриллионам, то есть почти в миллион раз больше. Следовательно, в данном случае намного легче получить беспорядок, чем получить порядок. Невольно вспоминается такое замечательное утверждение: «Яйца разбиваются на каждом шагу, но никто никогда не видел, чтобы ошмётки разбитого яйца сообрались вместе и стали целым яйцом. А всё потому, что есть только один способ получить целое яйцо и бесконечно много способов получить разбитое.
Обобщим замеченную нами закономерность:
В любом процессе, который происходит сам по себе, без дополнительного воздействия извне, скорее всего реализуется тот результат, которого можно достичь наибольшим числом способов.
Приглядитесь, это ведь тавтология во всей красе. Если все упростить, то я просто утверждаю, что «то, чему легче произойти, происходит чаще». Однако, это одновременно и один из важнейших физических законов. Многие из вас уже, наверное, поняли, что речь идет о втором начале термодинамики. Давайте посмотрим на одну из его «официальных» формулировок:
Энтропия замкнутой системы не может уменьшаться.
Теперь это меньше похоже на тавтологию, да? Но что же это за умное слово — энтропия?
Давайте представим воздух, заполняющий комнату. Он состоит из огромного количества молекул. Если мы мысленно разделим комнату на ячейки, мы получим трехмерный аналог игры в камни на очень большой доске с огромным количеством камней. Каждая позиция игры в данном случае называется макросостоянием системы.
Каждая из раскладок камней, реализующих ту или иную позицию — микросостояние. Возьмем два числа: число всех микросостояний, реализующих данное макросостояние и число всех возможных микросостояний. Если мы поделим первое на второе, мы получим вероятность реализации данного макросостояния.
Определение из книги: энтропией состояния системы называется логарифм вероятности реализации данного состояния.
Переведем на язык, понятный Гранту, — энтропия позиции это логарифм веса данной позиции. Попробуем сделать это ещё понятнее: чем большим числом способов можно получить позицию, тем больше энтропия.
Теперь мы видим, что книжная формулировка второго начала говорит следующее: от какой-либо позиции сам по себе может происходить только переход к такой позиции, которую можно получить большим чем или таким же числом путей, как и начальную.
Попробуем еще упростить: если мы потрясем доску, мы скорее получим такую позицию, какую легче получить.
Кажется, мы опять пришли к тавтологии.
Напоследок, давайте посмотрим еще пару формулировок второго начала:
- Постулат Клаузиуса: Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому
- Постулат Томсона: Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара.
Как видите, здесь уже нет тавтологии. И ни одна из них не очевидна. Однако, можно показать, что обе эти формулировки полностью равнозначны тавтологическому «наиболее вероятно, что произойдет то, вероятность чего больше». Иногда, для того, чтобы узнать что-то новое, нам нужно сначала осознать что-то очевидное.
В следующей части мы рассмотрим другую «научную тавтологию», которая, на первый взгляд, нарушает второе начало термодинамики.
Тавтология и плеоназм. В чём разница?
Сегодня поговорим о тавтологии и плеоназме. Если о первом понятии можно услышать в школьной программе, то о плеоназме упомянуть часто забывают.
Оба явления подразумевают под собой речевую избыточность. Конечно, бывают исключения, когда, например, тождесловие выступает определённой фигурой речи, призванной сделать акцент на том или ином предмете, но обычно такие ситуации хорошо считываются по контексту. Непреднамеренное же использование однокоренных слов считается ошибкой. Это своего рода речевая небрежность. Подобная несуразица считывается сразу, поэтому следует хорошо следить за построением предложений как в тексте, так и в речи (надеемся, вы уловили, что здесь не так с формулировкой).
Разберёмся в определениях
Тавтология — некорректное употребление однокоренных слов в речи, которые повторяют уже выраженный смысл. Другими словами, это определённое уточнение слов, необходимости в котором нет.
Примеры: масло масляное, вопросительно вопрошать, случайный случай, бежать бегом.
Плеоназм — понятие, переводимое как «излишество». Представляет собой речевой оборот, который основан на использовании в словосочетании близких семантически слов, в связи с чем создаётся неоправданный эффект логической избыточности. В языкознании плеоназм часто называют многословием, которое портит стиль («порок стиля»).
В таком случае мы не говорим о тождесловии, поскольку употребляемые слова не являются однокоренными: единицы, составляющие оборот, лишь повторяют значения друг друга в разной лексической форме. В результате уже выраженный смысл не получает уточнений, а лишь повторяется: нагрузка на словосочетание удваивается, речевая конструкция становится тяжеловесной и нелогичной.
В пределах оборота, который мы называем плеоназмом, вы не встретите однокоренных слов. Обычно это слова, делающие смысловую полноту высказывания избыточной.
Обратимся к примерам плеоназма: своя личная автобиография, другая альтернатива, в январе месяце, поднимается вверх, самый лучший.
Итак. Плеоназм — употребление заведомо лишнего слова, тавтология — ничем не оправданный (даже художественной выразительностью) повтор однокоренных слов в пределах одного предложения. Часто данные понятия отождествляются, но это в корне неверно. Плеоназм действительно можно считать более широким понятием, вбирающим в себя тавтологию, но разграничивать данные явления всё же необходимо.
Речевые ошибки, тавтология
Речевые ошибки: тавтология и плеоназмВ статье нет видимых ошибок, а заказчик остался недоволен, не пожелал оставить отзыв, не сказал пару тёплых слов. Виной всему речевая избыточность, коей грешат не только новички, но и зрелые авторы. Часто копирайтер долго, нудно, пространно рассуждает о том, что читателям «с младых ногтей» известно. Люди сразу утрачивают интерес и покидают сайт.
Разумеется, подобные статьи не нравятся заказчикам. Часто они в ТЗ пишут предупреждения, подобные этим:
Тавтология и плеоназмРечевая избыточность появляется от неумения копирайтера подобрать точные слова для выражения различных понятий. Писатели и хорошие авторы перебирают несколько вариантов, пока не остановятся на наиболее удачном термине, позволяющем точно, ёмко, лаконично выразить мысль.
Многие копирайтеры не занимаются подбором точных слов и их шлифовкой, поэтому пускаются в долгие объяснения. Им требуется намного больше слов и предложений, чтобы донести идеи/мысли до читателя. Так появляется речевая избыточность. Две её главные разновидности — плеоназм и тавтология.
Классный пример в картинках попался на глаза. Захотелось сплагиатить, чтобы показать райтерам, как не следует повторяться. Избыточность легко увидеть самостоятельно!
ПлеоназмПлеоназм переводится с греческого как излишество.
Термином обозначают употребление близких по смыслу слов, отсюда и проистекает избыточность. Самый распространённый плеоназм: так, например. Или фольклорные сочетания: на море-океане; путь-дорожка.
Иногда автор использует осознанно «мнимый плеоназм» (Не вернётся вспять время), чтобы усилить выразительность речи. Но не все читатели и заказчики это понимают. Хотя нарочитое несоответствие используется намеренно для привлечения внимания в надежде усилить эффект подобным выразительным приёмом.
ТавтологияРазновидность или частный случай плеоназма, когда повторяются однокоренные слова: «На остановке остановите, пожалуйста», «Я сейчас загадаю загадку». Дословный перевод термина тавтология — «то же самое слово».
Тавтологические ошибки проявляются, когда автор применяет слова, не зная их точного значения. Поэтому вычитка текста не поможет выявить и исправить допущенные неточности.
Не всегда повторы нужно устранять.
Иногда исключение однокоренного слова и его замена синонимом придаст тексту ещё большую нелепость, исказит смысл. Например, как иначе можно описать деятельность «варить варенье».
Слово «варенье» заменить на «джем» или «конфитюр»? Это искажение, а не полезная замена.
Стилистически оправдано употребление однокоренных слов, находящихся в близком контексте, и применение терминологических выражений, если к ним невозможно подобрать синонимы: словарь словообразования русского языка.
Борьба с тавтологиейК речевой избыточности относят частые повторения слов. Чаще всего их тоже называют тавтологией, хотя в копирайтинге для них есть собственный термин — тошнотность.
Недопустимо в одном предложении (и даже в рядом стоящих) использовать:
- повтор одного и тоже слова,
- однокоренных слов.
Борьба с тавтологией уместна, если чрезмерное употребление одиночного или однокоренных слов легко вызовет у читателя неприязнь и тошноту.
Хотя иногда повтор воспринимается необычно и забавно — в поэзии, юмористических текстах:
Я оглянулся посмотреть,
Не оглянулась ли она,
Чтоб посмотреть,
Не оглянулся ли я.
Проверка тавтологии: онлайн сервисыhttps://glvrd.ru/Сервис «Главред» помимо тавтологии поможет выявить ещё массу клише и ненужных слов, особенно в продающих текстах.
http://yourtext.ru/ustranit-tavtologiyu-onlajn.htmlУдобный сервис с примерами, поясняющий опасность тавтологии для копирайтера. Почему-то проигнорировал частые повторы слова «работа» и не заметил в последнем предложении в третий раз повторяющееся слово «специалисты».
http://quittance.ru/tautology.php#effectusРезультат после проверки «Свежего взгляда» (именно так называется услуга) такой же, как вердикт предыдущего сервиса.
Проверка тавтологии на трёх веб-сайтах показала не совсем удовлетворительный результат.
Трижды повторяющееся в двух предложениях слово «работа» осталось за порогом внимания.
Вывод: надеяться больше на себя, но не забывать использовать программы. Иногда они помогут увидеть то, что копирайтер упустил из-за невнимательности или усталости.
А если тавтология, по мнению автора, применена, чтобы усилить экспрессию, а заказчик этого не понял, можно ему пояснить, для чего использован «запрещённый» приём.
«Работа копирайтером» приглашает к прочтению других статей:
| |||||||||||||||||
| LiveJournal.com | |||||||||||||||||
А некрасивые обязаны быть счастливыми. Потому что некрасивые и несчастные — это банальность, почти пошлость, одним словом, моветон».
Теперь счастливо им обладаю, трехтомником.Тавтология — Academic Kids
от академических детей
В логике тавтология — это утверждение, которое истинно по своему собственному определению и поэтому в корне неинформативно. Логические тавтологии используют круговые рассуждения в аргументе или утверждении.
В лингвистике тавтология — это избыточность из-за излишней квалификации.
Логические тавтологии
Логическая тавтология — это утверждение, которое истинно независимо от значений истинности его частей.Например, утверждение «Все вороны либо черные, либо не черные» является тавтологией, потому что оно верно независимо от цвета вороны. В качестве юмористического примера, тавтология известна как «то, что тавтологично». (Это определение, конечно, тавтологично.) В более реалистичном примере, если бы биолог определил «соответствие» во фразе «выживание наиболее приспособленных» как «с большей вероятностью выживет», это определение было бы тавтологией.
Противоположностью тавтологии является противоречие, то есть утверждение, которое всегда ложно, независимо от значений истинности его частей.
Тавтологии могут быть использованы для отвлечения внимания в споре, но они не являются взаимоисключающими.
Противоречие
Что является логической тавтологией, а что нет, может быть предметом ожесточенных споров. Рассмотрим пример «полезной помощи». Если бы это был ключевой термин в систематическом мышлении какого-нибудь философа, критик мог бы счесть его сокрушительным возражением, чтобы указать на его тавтологический характер. И все же философ мог бы ответить: «Это явно не тавтология, потому что бесполезная помощь тоже существует — большинство из нас стали жертвами достаточно неудач, чтобы получать ее время от времени!»
Менее гипотетически вопрос о том, тавтологичны или существенны такие утверждения, как «только свободный рынок может определить истинную стоимость товара», широко обсуждался в социальной философии.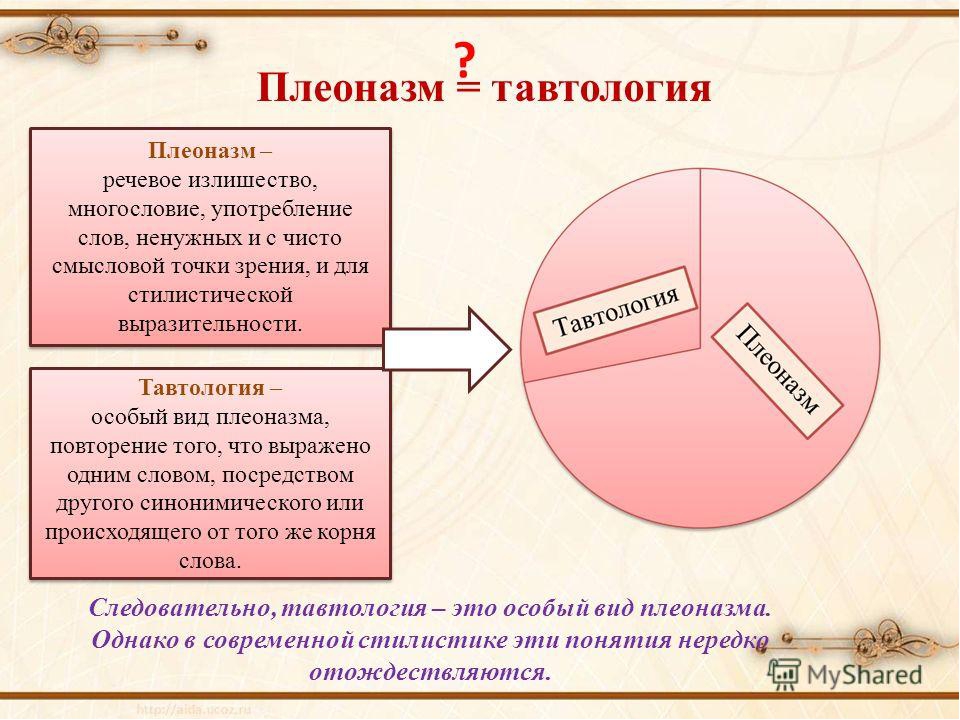
Тонкость
Споры возникают из-за того, что иногда логическая тавтология может быть довольно тонкой. Предположим, что аналитик новостей должен был сделать следующее заявление:
- Все основные сенаторы США согласны с тем, что законопроект Палаты представителей неприемлем.
Казалось бы, это содержательное утверждение. Но предположим далее, что он также должен был раскрыть свое мнение о том, что сенатор К. «не согласен с этим и поэтому показал себя вне мейнстрима. В данном случае определение аналитика «мейнстрима» требует несогласия с законопроектом Палаты представителей. Поэтому его первоначальное заявление было тавтологией.
Не вижу настоящего шотландца
Лингвистические тавтологии
Лингвистическая тавтология часто является ошибкой стиля. Это было определено Фаулером как «повторение одного и того же дважды». Например, «трилогия из трех частей» тавтологична, потому что трилогия, по определению, состоит из трех частей (за исключением случая шутливо названного «Автостопом по галактике», «трилогии» из 6 частей).
«Значительная веха» и «значительный ориентир» также, хотя и менее очевидно, тавтологичны, потому что вехи и ориентиры снова значимы по определению (можно ли представить себе «незначительный ориентир»?).
Тавтологии иногда возникают при совместном использовании нескольких языков, таких как «The La Brea Tar Pits» ( the tar tar pits ), «Sierra Nevada Mountains» ( снежных гор, ), « Manos: The Hands» Судьбы »( рук: руки судьбы ),« Ангелы Лос-Анджелеса »( ангелы ангелов ) или« Собака Шиба-ину »( маленькая собачка ).Они часто появляются в сочетании с акронимами или аббревиатурами, когда первоначальное значение исчезает из-за знакомства с самим акронимом; например, рассмотрите «банкомат», «номер PIN», «язык HTML», «номер VIN», «NT Techonology» (выражение, фактически используемое Microsoft) или «ЖК-дисплей». (См. Синдром РАС.) Другие примеры лингвистических тавтологий включают «в наши дни», «полезная помощь» и «новые инновации». Многие из этих примеров также являются моделями плеоназма.
Лингвистическая тавтология может быть направлена на усиление или подчеркивание определенного аспекта обсуждаемой вещи: например, подарок по определению является бесплатным, но можно говорить о «бесплатном подарке», если тот факт, что денег не было платный имеет особое значение.Тавтология также может использоваться, если нетавтологичное выражение не может быть принято за чистую монету: например, компания может предложить своим клиентам «бесплатный подарок», чтобы отличаться от других компаний, которые заявляют, что предлагают «подарки», но только дарить их вместе с покупкой. Точно так же можно использовать тавтологию, если нетавтологичное выражение может быть двусмысленным или непонятным: хотя PIN означает «Персональный идентификационный номер», можно ссылаться на «PIN-номер», если целевая аудитория не знакома с аббревиатуру, или чтобы не путать со словом pin … или на юге Соединенных Штатов, где «ручка» и «булавка» часто произносятся почти одинаково, отсюда и использование очевидной тавтологии «чернильное перо».
По этим причинам, хотя тавтологии технически не нужны и могут считаться неправильными, они, тем не менее, обычны в некоторых контекстах.
В одном из мультфильмов Дилберта это доведено до юмористической крайности. Дилберт говорит, что работает над проектом, который известен как «ТТП». На вопрос, что означает «TTP», Дилберт отвечает, что это означает « T he T TP P roject».Если бы эта бесконечная прогрессия достигла своего конца, возможно, обнаружится, что эта неуловимая вторая буква «Т» обозначает «тавтологию».
См. Также
Внешняя ссылка
cs: тавтология de: Tautologie fr: Tautologie это: Тавтология nl: Tautologie pl: Tautologia pt: Tautologia sv: Tautologi
1.1.10: Классификация предложений — Engineering LibreTexts
Определенные типы предложений будут играть особую роль в нашей дальнейшей работе с логикой.В частности, мы определяем тавтологии, противоречия и случайности следующим образом:
Определение 2.
4.
Составное суждение называется тавтологией тогда и только тогда, когда оно истинно для всех возможных комбинаций значений истинности пропозициональных переменных, которые оно содержит. Сложное предложение называется противоречием тогда и только тогда, когда оно ложно для всех возможных комбинаций значений истинности пропозициональных переменных, которые оно содержит.Сложное суждение называется случайностью тогда и только тогда, когда оно не является ни тавтологией, ни противоречием.
Например, предложение (( p ∨ q ) ∧ ¬ q ) → p является тавтологией. Это можно проверить 2 с помощью таблицы истинности:
Тот факт, что все записи в последнем столбце верны, говорит нам, что это выражение является тавтологией. Обратите внимание, что для любого составного предложения P , P является тавтологией тогда и только тогда, когда ¬ P является противоречием.
(Здесь и в будущем я использую прописные буквы для обозначения сложных предложений. P обозначает любую формулу, состоящую из простых предложений, пропозициональных переменных и логических операторов.)
Логическая эквивалентность может быть определена с помощью тавтологии:
Определение 2.5.
Два составных предложения, P и Q , называются логически эквивалентными тогда и только тогда, когда предложение P ↔ Q является тавтологией.
Утверждение, что P логически эквивалентно Q , будет символически выражено как « P ≡ Q ». Например, ( p → q ) ≡ (¬ p ∨ q ) и p ⊕ q ≡ ( p ∨ q ) ∧ ¬ ( p ∧ q ).
Что делать, если P → Q и P ложны? Из ложной посылки мы можем сделать любой вывод (проверьте таблицу истинности →).
Итак, если k означает «Я король Нидерландов», тогда k → Q верно для любого составного предложения Q . Вы можете заменить Q чем угодно, и импликация k → Q останется в силе. Например, логически верный вывод: «Если я король Нидерландов, значит, единороги существуют». Идя дальше, из противоречия можно сделать любой вывод. Это называется Принцип взрыва .
Упражнения
1. Приведите три таблицы истинности, определяющие логические операторы ∧, ∨ и ¬.
2. Некоторые из следующих сложных суждений являются тавтологиями, некоторые — противоречиями, а некоторые — ни тем, ни другим (т. Е. Случайностями). В каждом случае используйте таблицу истинности, чтобы решить, к какой из этих категорий относится предложение:
a) ( p ∧ ( p → q )) → q b) (( p → q ) ∧ ( q → r )) → ( p → р )
c) p ∧ ¬ p d) ( p ∨ q ) → ( p ∧ q )
e) p ∨ ¬ p f) ( p ∧ q ) → ( p ∨ q )
3.
Используйте таблицы истинности, чтобы показать, что каждое из следующих утверждений логически эквивалентно p ↔ q .
a) ( p → q ) ∧ ( q → p ) b) ¬ p ¬ q
c) ( p → q ) ∧ (¬ p → ¬ q ) d) ¬ ( p ⊕ q )
4. Является ли → ассоциативная операция? Это is ( p → q ) → r логически эквивалентно p → ( q → r )? Является ли↔ ассоциативным?
- Пусть p представляет предложение «Вы уходите», а пусть q представляет предложение «Я ухожу».Выразите следующие предложения как составные предложения, используя p и q , и покажите, что они логически эквивалентны:
а) Либо ты уйдешь, либо я уйду. (Или оба!) Б) Если ты не уйдешь, я уйду.
- Предположим, что m представляет утверждение «Земля движется», c представляет «Земля является центром вселенной», а g представляет «Галилей был ложно обвинен».
Переведите на английский каждое из следующих составных предложений:
Переведите на английский каждое из следующих составных предложений:а) ¬ г ∧ в б) м ¬ в
c) м ↔ ¬ c d) ( м → г ) ∧ ( c → ¬ г )
7.Дайте обратное и противоположное для каждого из следующих английских предложений:
а) Если у вас все хорошо, Синтерклаас принесет вам игрушки.
б) Если посылка весит более одного килограмма, вам потребуется дополнительная оплата.
в) Если есть выбор, я не ем кабачки.
8. В обычной колоде из пятидесяти двух игральных карт для скольких карт верно а) что «Эта карта — десятка, а эта карта — сердце»?
б) что «Эта карта — десятка или эта карта — сердце»?
c) что «Если эта карта — десятка, то эта карта — сердце»?
d) что «Эта карта — десятка, если и только если эта карта — сердце»?
9.Определите логический оператор ↓ так, чтобы p ↓ q было логически эквивалентно ¬ ( p ∨ q ).
(Этот оператор обычно называют «ни», сокращенно от «не или».) Покажите, что каждое из предложений ¬ p , p q , p ∨ q , p → q , p ↔ q и p ⊕ q можно переписать как логически эквивалентное утверждение, в котором ↓ используется в качестве единственного оператора.
10. Для нашего доказательства функциональной полноты {¬, ∨} нам нужно показать, что все формулы в пропозиционной логике могут быть выражены в эквивалентной форме, используя только {¬, ∧, ∨, →, ↔}.
а) Сколько существует уникальных таблиц истинности для формул, содержащих два атома?
b) Создайте функцию для каждой из возможных таблиц истинности, которая использует только 5 перечисленных операторов
выше.
c) Приведите (неформальный) аргумент, почему это означает, что все формулы в логике высказываний могут быть
выражается с использованием только этих пяти операторов.
Глоссарий социальных исследований
_________________________________________________________________
Тавтология
определение ядра
Тавтология — это суждение, истинное по определению (например, «все матери — женщины») или предложение, в котором одно и то же повторяется дважды разными словами (например, «они следовали одно за другим последовательно»).
пояснительный контекст
Тавтология может быть расширена до целого аргумента. В котором
в случае, если исход тавтологического аргумента будет логически
всегда быть правдой, независимо от того, правда или ложь
предложения.
Простой пример: «Либо вся трава зеленая, либо нет. А
более сложный пример символически представлен следующим образом:
(p или q) или не-p,
где не имеет значения, какая комбинация истинного или ложного
присвоенный p и q результат будет истинным.
Тавтологии истинны из-за природы логических операторов, независимо от правдивости предположений, сделанных о реальном мире. Это привело к тому, что тавтологии стали рассматриваться как пустые, ничего не говорящие и не имеющие отношения к развитию. знания о мире.
аналитический обзор
Стэнфордская энциклопедия философии (2017) объясняет различие между аналитикой и синтетикой следующим образом:
Тавтология , по логике, утверждение, сформулированное так, что его нельзя отрицать без противоречия.Таким образом, выражение «Все люди — млекопитающие» должно утверждать в отношении чего бы то ни было, что либо это не человек, либо млекопитающее. Но эта универсальная «истина» следует не из каких-либо фактов о реальных людях, а только из фактического использования человека и млекопитающего и, таким образом, является чисто вопросом определения.
. В исчислении высказываний — логика, в которой все предложения связаны такими связками, как ⊃ («если… то»), · («и»), ∼ («не») и ∨ («или»), даже сложные выражения, такие как [( A ⊃ B ) · ( C ⊃ ∼ B )] ⊃ ( C ⊃ ∼ A ), могут быть показаны как тавтологии, отображая в таблице истинности каждый возможная комбинация значений истинности — T (истина) и F (ложь) — ее аргументов A, B, C и после вычисления с помощью механического процесса истинностного значения всей формулы, отмечая, что , для каждой такой комбинации формула T .
Тест эффективен, потому что в любом конкретном случае общее количество различных присвоений истинностных значений переменным конечно, и вычисление истинностного значения всей формулы может выполняться отдельно для каждого присвоения истинности. ценности.
Понятие тавтологии в исчислении высказываний было впервые разработано в начале 20 века американским философом Чарльзом Сандерсом Пирсом, основателем школы прагматизма и крупным логиком. Сам термин, однако, был введен британским философом австрийского происхождения Людвигом Витгенштейном, который утверждал в Logisch-Philosophische Abhandlung (1921; Tractatus Logico-Philosophicus , 1922), что все необходимые предложения являются тавтологиями и что они существуют. следовательно, в смысле, в котором все необходимые предложения говорят об одном и том же, а именно, вообще ничего….
связанных проблем
смежные области
См.
Также
логика
правда
Источники
Британская энциклопедия, 2019 г., ‘Tautology’, обновлено 28 мая 2019 г., доступно по адресу https://www.britannica.com/topic/tautology, по состоянию на 15 июня 2019 г.
авторское право Ли Харви 2012–2020
A NOVEL
Верх
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Дом
Тавтология {Philosophy Index}
Тавтология в логике — это формула, которая всегда верна при любой оценке или интерпретации ее терминов.Их также иногда называют действительными формулами (не путать с действительным аргументом) или логическими истинами
Наиболее очевидным и часто используемым примером тавтологии является формула A ¬A . При любой оценке, истинно ли А или ложно, А или нет-А всегда будет истинным утверждением.
Мы можем легко проверить, что A ¬A является тавтологией, с помощью таблицы истинности:
В противном случае тавтологию можно определить как формулу, которая удовлетворяется при каждой возможной оценке.
Мы можем формально указать, что формула φ является тавтологией на φ . Символ ⊤ или буква «Т» также используются для обозначения тавтологии.
«Тавтология», термин
Термин тавтология первоначально использовался в риторике для обозначения утверждений, которые сами по себе являются избыточными. Например, фраза «неразгаданная тайна» является риторической тавтологией, потому что любая тайна остается неразгаданной — прилагательное не имеет смысла и не добавляет смысла фразе.То же самое обычно происходит с акронимами. Например, аббревиатура ATM означает «банкомат». Таким образом, общая фраза «банкомат» является риторической тавтологией, поскольку они по сути говорят «банкомат». То же самое происходит с «форматом PDF», «PIN-кодом» и «UPC-кодом».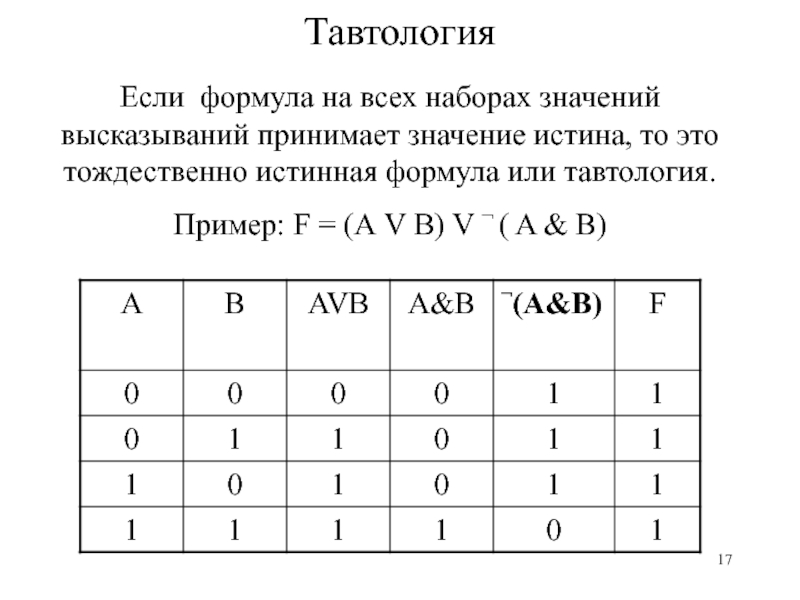
Это, конечно, отличается от логической тавтологии, но этот термин перекочевал в логику благодаря утверждению, что логические тавтологии по сути являются бессмысленными утверждениями. Они не предоставляют никакой информации или, по крайней мере, никакой новой информации.Сделать тавтологичное утверждение: «На моей голове либо шляпа, либо нет шляпы на голове» — значит сказать что-то правдивое, не говоря ничего значимого. Из этого утверждения мы ничего не узнаем о состоянии головных уборов и головных уборов.
Использование термина тавтология в логике высказываний можно приписать Витгенштейну.
Тавтология 101 — Содержание BKA
Если вы посещали государственную школу в течение последних 40 лет, вы, вероятно, подвергались воздействию мотивационного оратора.Возможно, он сидел в тюрьме. Возможно, он знал немного магии легкости в использовании. У него, вероятно, были усы, и он почти наверняка кричал вам и вашим товарищам из 6 классов -го : «Это то, что есть!» и «Если ты будешь употреблять наркотики, ты либо останешься таким же, как я, либо нет!» Другими словами, то, чего ему не хватало в истинном вдохновении, он восполнял, демонстрируя значение тавтологии.
Что такое тавтология?
Что такое определение тавтологии? Тавтология — это повторяющееся слово или фраза, которые ничего не добавляют к вашему письму.Он бывает двух видов: логический и риторический.
1. Логическая тавтология — это утверждение, которое верно во всех ситуациях.
Когда мнение истинно, независимо от того, как вы его интерпретируете, это называется логической тавтологией. Выглядит это так:
- Либо на начо есть сметана, либо на начо нет сметаны.
Ну, без шуток. Это предложение справедливо буквально для любой тарелки начо.Вот что делает его логической тавтологией. Как бы то ни было, тарелку восхитительных начо из грудинки либо испортила большая капля сметаны, либо нет.
Примеры логической тавтологии:
Давайте отбросим мою ненависть к сметане и рассмотрим еще несколько примеров, определяющих тавтологию логического типа:
- Отправляясь в отпуск, мы, скорее всего, поедем на Багамы или еще куда-нибудь.
Да, конечно. Потому что — от Диснейленда до крайних пределов Сибири — повсюду на Земле, кроме Багамских островов в этом примере, подпадает под зонтик «где-то еще.”
- Дженна, я посмотрела на результаты твоих анализов, и эта болезнь зомби-плотоядных убьет тебя или нет.
Если она не горец, что-то в конечном итоге убьет Дженну, поэтому заявление ее врача верно, как бы вы его ни интерпретировали. Верно и то, что Дженне нужен новый врач, STAT.
2. Риторическая тавтология использует несколько слов, чтобы сказать одно и то же.
Непреднамеренное повторение одной и той же мысли разными словами — пример риторической тавтологии.Это не самый лучший наполнитель. Это излишне и абсолютно ничего не делает для улучшения вашего письма.
Примеры риторических тавтологий
Давайте рассмотрим четыре примера риторической тавтологии:
- Шлем — необходимое требование для игры в хоккей.
Если нужно играть (и сохранить хотя бы пару зубов), то играть по определению необходимо.
Если ты умеешь кричать тихо, напиши меня в Твиттере, потому что я хочу, чтобы ты научил моего малыша твоим загадочным способам.
- Директор лично посетил Брейдена.
Я знаю, о чем вы думаете: а как насчет голограмм? Хорошая попытка. Директор не может посетить Брейдена, не приведя его с собой.
- Вы просто лучший — лучше всех.
Приношу свои извинения Тине Тернер: «Лучше, чем все остальное» — это определение «лучший», что делает этот припев ярким примером риторической тавтологии.
Ознакомьтесь с этими 12 распространенными примерами риторической тавтологии
В лучшем случае тавтология в вашем письме может заставить вас казаться дилетантским.В худшем случае это может подорвать ваш авторитет. Вот набор из 12 распространенных примеров тавтологии, которые могут нанести ущерб вашему письму.
- Дженис Джоплин умерла от фатальной передозировки героина.
- Best Buy — это , раздача бесплатно плееров iPod.
- Сначала и , прежде всего , нам нужно определиться с названием команды.
- В течение многих лет Кевин скрывал от своих друзей, что он был секретным Hootie и фанатом Blowfish.
- Когда я был ребенком, YouTube был новой инновацией .
- Пожалуйста, предоплата заранее перед прокачкой газа.
- По моему мнению, , Я думаю, что Деннис Родман — лучший баскетболист всех времен.
- Педикюр у моей собаки: 10:00 . утром .
- После того, как наш официант чихнул в в непосредственной близости от салат-бара, я переключил свой заказ на гамбургер.
- Назад в будущее: Часть II сделал несколько точных прогнозов о будущем .
- Все большие пиццы идут с добавленным бонусом хлебных палочек.
- Меган получила баллов, достаточно , чтобы поступить в Университет Сэма Уотерстона.
Помните: не все повторения — тавтология
Иногда писатели и ораторы специально повторяют слова или фразы. Расстроенная мать может повторить себя, чтобы выразить свое разочарование, например:
- Тайлер, если ты не уберешь свои грязные носки с кухонной стойки, я брошу ключи от твоей машины в озере Мичиган.В озере! Мичиган!
Здесь повторение «озера Мичиган» намеренно и используется, чтобы передать разочарование мамы по поводу ее отвратительного сына Тайлера, поэтому это не соответствует определению тавтологии. Скорее, этот тип преднамеренного повторения называется эпистрофом, причудливым греческим словом, описывающим повторение в конце предложения, сделанное для достижения эффекта.
Пример эпистрофа
Давайте посмотрим на другой пример эпистрофа:
- Когда я прошу Тайлера принять душ, он говорит, что сделает это после еще одного эпизода. Каждый раз, «после еще одной серии».
Каждый раз, «после еще одной серии». В этом примере бедная мать Тайлера использует повторение, чтобы выразить свое недовольство, а также то, насколько он полон, по ее мнению, ее вонючий сын-подросток.
Писатели и ораторы могут также использовать повторение в начале предложения, чтобы придать ему дополнительный смысл. Когда это происходит, это называется анафорой. Давайте посмотрим на два примера анафор:
Примеры анафор
- Дженнифер Лопес умеет петь.Дженнифер Лопес умеет танцевать. Дженнифер Лопес умеет играть. Дженнифер Лопес умеет приготовить подлый куриный буйабес.
Повторение фразы «Дженнифер Лопес может» в этом примере используется, чтобы подчеркнуть, насколько она талантлива.
- Каждый Хэллоуин ты заставляешь меня одеваться как Джа-Джа Бинкса. Каждый Хэллоуин я делаю, как мне говорят. Каждый Хэллоуин я хочу купить яблоко и никогда больше не всплывать.
В этом примере говорящий повторяет «каждый Хэллоуин», чтобы выделить три момента: Во-первых, вся эта ситуация длилась слишком долго.
Во-вторых, он или она был хорошим спортсменом, год за годом снося усталый костюм из «Звездных войн». В-третьих, все должно измениться, если они собираются и дальше проводить вместе Хэллоуин.
Тавтология: обычно достаточно
От поп-музыки до политики — тавтология повсюду — просто спросите Йоги Берра. Дело в том, что этим непреднамеренным повторам нет места практически ни в какой форме письма. Чтобы сохранить доверие к себе, добавьте в свой распорядок проверки тавтологию.
Хотите поделиться лучшими советами по борьбе с тавтологией? Есть какие-нибудь любимые примеры тавтологии? Попади в раздел комментариев ниже!
Тавтологии, противоречия и условности
Свойства предложений: тавтологии, противоречия и условности
Мы увидели, как использовать таблицы истинности и тест присвоения истинности, чтобы определить, является ли аргумент допустимым или недопустимым. Эти же инструменты также позволяют нам исследовать логические свойства отдельных предложений и логические отношения между предложениями.
Ниже рассматриваются логические свойства предложений; некоторые важные логические отношения будут представлены на следующей странице.
Предложения можно разделить на три категории: тавтологии, противоречия и случайности. Является ли предложение тавтологией, противоречием или случайностью, зависит от его формы — логической структуры.
Тавтология , или тавтологическое суждение , имеет логическую форму, которая не может быть ложной (независимо от того, какие значения истинности присваиваются буквам предложения).
Следующие предложения являются тавтологиями:- (A ⊃ A)
- (A ∨ ~ A)
- ~ (А • ~ А)
- ((A • B) ⊃ (A ∨ B))
- ((A ∨ B) ≡ (B ∨ A))
Противоречие , или противоречивое суждение , имеет логическую форму, которая не может быть истинной (независимо от того, какие значения истинности присваиваются буквам предложения).
Следующие утверждения являются противоречиями:- (А • ~ А)
- ~ (A ∨ ~ A)
- ~ (А ⊃ А)
- ((A ∨ ~ A) ⊃ (B • ~ B))
- ~ ((A ∨ B) ≡ (B A))
Условное предложение или условное предложение имеет логическую форму, которая может быть истинной или ложной (в зависимости от того, какие значения истинности присвоены буквам предложения).
Следующие предложения являются непредвиденными:- А
- ~ А
- (A ∨ B)
- ~ (A • B)
- (A ⊃ B)
- ((A ∨ B) ⊃ (C • D))
- ((A • B) ≡ (C ∨ D))
Некоторые предложения имеют логическую структуру, которая не может быть представлена функциональными связками истинности, и по этой причине некоторые тавтологии и противоречия выглядят как случайности, когда они символизируются в логике высказываний.В следующих главах мы будем иметь дело с другими видами логической структуры.
Чтобы определить, является ли предложение тавтологией, противоречием или случайностью, мы можем построить для него таблицу истинности. Если утверждение верно в каждой строке таблицы, это тавтология. Если он ложен в каждой строке, значит, противоречие. И если предложение не является ни тавтологией, ни противоречием, то есть если есть хотя бы одна строка, где оно истинно, и хотя бы одна строка, где оно ложно, то утверждение является случайностью.
Если розы красные, а фиалки синие, то розы не красные.
Это может звучать как противоречие — утверждение, которое не может быть правдой. Однако наши интуитивные представления о логических свойствах часто ошибочны. Чтобы выяснить, что это за тип предложения, давайте обозначим предложение символами и построим для него таблицу истинности:
| R | B | ((R • B) ⊃ ~ R) | ||
|---|---|---|---|---|
| 0 | 0 | 1 | ||
| 0 | 1 | 1 | 908 | 1 |
| 1 | 1 | 0 |
Как видно из приведенной выше таблицы истинности, утверждение определенно не противоречит.Фактически, существует больше способов сделать это истинным, чем ложным: это истинно в каждой строке, кроме последней. Поскольку это истинно по крайней мере в одной строке и ложно по крайней мере в одной строке, это случай .
Давайте рассмотрим еще несколько примеров.
В следующей таблице истинности показаны возможные значения истинности для трех составных суждений. Одно из предложений — тавтология, одно — противоречие, а третье — случайность. Вы можете сказать, что есть что?
| A | B | C | (~ (A ∨ B) • B) | ((A • B) ∨ C) | (B ⊃ (B ∨ C)) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | ||||
| 0 | 0 | 1 | 0 | 1 | 1 | ||||
| 1 | |||||||||
| 0 9088 0 | 1 | ||||||||
| 0 | 1 | 1 | 0 | 1 | 1 | ||||
| 1 | 0 | 0 | 00 | 00 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 |
Профессиональный position (~ (A ∨ B) • B) противоречие, потому что оно ложно во всех строках.
(В соответствующем столбце таблицы их нет.)
Утверждение ((A • B) ∨ C) является случайностью, потому что оно истинно в одних строках и ложно в других.
Предложение (B ⊃ (B ∨ C)) является тавтологией, потому что оно истинно в каждой строке. (В его столбце нет нулей.)
В качестве альтернативы мы можем использовать метод присвоения истинности, чтобы определить, является ли предложение тавтологией, противоречием или случайностью. Вместо того, чтобы строить всю таблицу истинности, мы можем просто проверить, возможно ли, чтобы предложение было ложным, а затем проверить, возможно ли, чтобы предложение было истинным.Вот описание процедуры более подробно:
- Чтобы проверить, является ли предложение тавтологией , нам нужно определить, возможно ли, чтобы предложение было ложным. (Помните, тавтология имеет форму, которая не может быть ложной.) Итак, мы начинаем с присвоения «0» ее главной связке, а затем вычисляем значения истинности любых других связок и букв предложения, которые могут быть определены на основе этого предположение. Если некоторые буквы не могут быть вычислены, попробуйте все возможные комбинации значений для этих букв, чтобы увидеть, есть ли какой-либо способ сделать предложение ложным.Если нет способа опровергнуть утверждение, это тавтология. Но если вам удастся найти способ сделать предложение ложным, это не тавтология, поэтому вам следует перейти к шагу 2:
- Чтобы проверить, является ли предложение противоречием , начните с присвоения «1» его главной связке, затем вычислите значения истинности любых других связок и букв предложения, которые могут быть определены на основе этого предположения. Если некоторые буквы не могут быть вычислены, попробуйте все возможные комбинации значений для этих букв.Если нет способа сделать предложение истинным, это противоречие. Но если вам удастся найти способ, чтобы утверждение было истинным, это не противоречие.
- Если предложение не является ни тавтологией, ни противоречием, как определено в шагах 1 и 2, то это случай .
Если некоторые буквы не могут быть вычислены, попробуйте все возможные комбинации значений для этих букв, чтобы увидеть, есть ли какой-либо способ сделать предложение ложным.Если нет способа опровергнуть утверждение, это тавтология. Но если вам удастся найти способ сделать предложение ложным, это не тавтология, поэтому вам следует перейти к шагу 2:
Либо розы красные, а фиалки синие, либо розы красные, только если фиалки не синие.
Помните, тавтология имеет логическую форму, которая не может быть ложной.Итак, чтобы определить, является ли это утверждение тавтологией, нам нужно проверить, есть ли какой-либо способ сделать его ложным. Чтобы выяснить это, давайте обозначим его символами и присвоим его основному соединительному элементу «0»:
| (( | R | • | B | ) | ∨ | ( | R | ⊃ | ~ | B | ) 83 | 9082 | 9082 | 80 |
«∨» может быть ложным только одним способом, а именно, если оба дизъюнкта ложны:
| (( | R | • | B | ) | ∨ | ( | R | ⊃ | ~ | B | ) 83 | 00 |
Более того, «⊃» может быть ложным только одним способом, а именно, если R истинно, а ~ B ложно (и, следовательно, B истинно).
Это означает, что если утверждение в целом ложно (как мы предполагали), то R и B оба должны быть истинными. Однако, если мы сделаем R и B истинными, то (R • B) больше не будет ложным, и, следовательно, «∨» тоже больше не будет ложью:
| (( | R | • | B | ) | ∨ | ( | R | ⊃ | ~ | B | 1 | 0 | 1 | 0 | 0 | 1 |
Итак, нет возможности сделать это предложение ложным.Это тавтология.
Тавтология | Encyclopedia.com
oxford
просмотров обновлено 17 мая 2018 tau · tol · o · gy / tôˈtäləjē / •
п. (мн. -г.) повторение одного и того же дважды разными словами, как правило, считается стилистической ошибкой (например, они поступали одно за другим последовательно ). ∎ фраза или выражение, в которых одно и то же повторяется дважды разными словами.
∎ Логика — утверждение, которое является истинным по необходимости или в силу своей логической формы. ПРОИЗВОДНЫЕ: tau · to · log · i · cal / ˌtôtlˈäjikəl / adj.tau · to · log · i · cal·ly / ˌtôtlˈäjik (ə) lē / adv.tau · tol · o · gist / -jist / n .tau · tol · o · gize / -ˌjīz / v.tau · tol · o · gous / -gəs / прил.
The Oxford Pocket Dictionary of Current English
oxford
просмотров обновлено 14 мая 2018 г. TAUTOLOGY, также PLEONASM. Термин в RHETORIC для ненужного и неэффективного ПОВТОРЕНИЯ, обычно со словами, которые не добавляют ничего нового: Она была одна .Многие тавтологические (или тавтологические) выражения встречаются в повседневном употреблении. Сразу бросается в глаза тавтология в некоторых: все хорошо ; прикольные , спокойные , и собранные ; бесплатно , бесплатно , и бесплатно . В других менее очевиден, потому что они содержат архаичные элементы: всеми правдами и неправдами ; оттенок и крик ; ни чеканка, ни чеканка ; недействительна ; Стойка и развалина .
Сравните ОКРУЖЕНИЕ, ИЗБЫТОЧНОСТЬ. Краткий оксфордский компаньон английского языка Том Макартур
оксфорд
просмотров обновлено 23 мая 2018 г. тавтология Использование слов для повторения (без необходимости) одного и того же утверждения или значения. Например, утверждение, что «Британия — это остров, окруженный водой», является тавтологией, поскольку так описываются острова по определению. Тавтологические объяснения так же верны по определению или циркулярны, а потому не поддавались опровержению.Социологические объяснения, которые определяют истоки социальных институтов в их последствиях, имеют тенденцию принимать эту форму. Так, например, некоторые ранние антропологи-функционалисты (включая Бронислава Малиновского) были склонны утверждать, что, поскольку существовали определенные (экзотические) социальные практики (такие как колдовство), то они должны иметь социальную функцию — и что можно предположить, что они выполняли эту функцию.
функционируют именно потому, что существовали сами практики. Социологический словарь ГОРДОН МАРШАЛЛ
оксфорд
просмотров обновлено: 18 мая 2018 г. тавтология Закон логики в форме предложения, который описывает универсальную истину; независимо от того, какие значения присвоены переменным в предложении, результат всегда верен.Пример из исчисления высказываний: ( P ∨ Q ) ′ = P ′ ∧ Q ′, где ∨ и ∧ — это операторы или , а также и , а P ′ — отрицание. из П . В таблице истинности для тавтологии столбец окончательного результата содержит только истинное значение. Если последний столбец содержит только значение false, то обнаружено противоречие .
Компьютерный словарь ДЖОН ДЕЙНТИТ
оксфорд
просмотров обновлено 29 мая 2018 г. тавтология XVI.- поздний Л. тавтология — Гр. tautologíā , ф.