Не ломай голову: готовый алгоритм для решения проблем любой сложности :: РБК Pro
Pro Партнер проекта*
Телеканал
Pro
Инвестиции
Мероприятия
РБК+
Новая экономика
Тренды
Недвижимость
Спорт
Стиль
Национальные проекты
Город
Крипто
Дискуссионный клуб
Исследования
Кредитные рейтинги
Франшизы
Газета
Спецпроекты СПб
Конференции СПб
Спецпроекты
Проверка контрагентов
РБК Библиотека
Подкасты
ESG-индекс
Политика
Экономика
Бизнес
Технологии и медиа
Финансы
РБК КомпанииРБК Life
Материал раздела Основной
Саморазвитие   · Гибкие навыки
Инструкции Business Speech
Одна из самых востребованных компетенций топ-менеджера — «комплексное решение сложных проблем». Я дам алгоритм, который поможет вам найти оптимальный способ решения проблемы, не хватаясь за первый пришедший в голову
Я дам алгоритм, который поможет вам найти оптимальный способ решения проблемы, не хватаясь за первый пришедший в голову
Некоторые исследователи отделяют термин «комплексное решение проблем» (complex problem solving) от другого — «принятие решений» (decision making), подразумевая, что между ними есть некая смысловая разница. Безусловно, некоторые механизмы обеих компетенций отличаются, однако фундамент у них общий. Поэтому я умышленно отождествляю «решение проблем» и «принятие решений», пользуясь нехитрым принципом: «Правильные решения устраняют проблемы». Что же такое проблемы? И почему так важно правильно с ними работать?
Под проблемой я понимаю некую трудность, которая не дает получить желаемое. Это может быть отсутствие готового решения, неудовлетворительное состояние текущих дел, непонимание достижения своей цели.
1) решить проблему;
2) изменить свое отношение к проблеме;
3) проигнорировать проблему.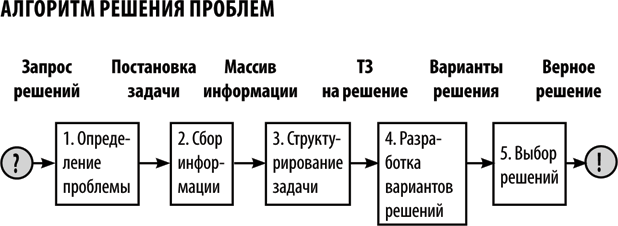
Я очень люблю фразу: «Если не можешь изменить ситуацию, измени свое отношение к ней». Она идеально описывает, как надо поступить, если нам не под силу решить проблему. Некоторые проблемы и вовсе не имеют решения. Поэтому их мы просто игнорируем, ведь жизнь одна, а время ограничено. Но понятие problem solving все же подразумевает поиск наилучшего решения проблемы.
Предлагаю алгоритм решения проблем, состоящий из пяти логичных шагов.
АЛГОРИТМ ЭФФЕКТИВНОГО РЕШЕНИЯ ПРОБЛЕМ [ТРАБЛХАКИНГ]
Базовый метод совершенствования и исследования
внешних систем
Термины
Алгоритм эффективного решения проблем (АЭРП)― это научно-исследовательский метод траблхакинга, позволяющий путем глубокого анализа нетехнических систем изобрести нестандартные способы решения задач. Алгоритм основан на системном анализе, теории рисков и инструментах Теории решения изобретательских задач (ТРИЗ).
Алгоритм основан на системном анализе, теории рисков и инструментах Теории решения изобретательских задач (ТРИЗ).
Ядро цели ― метод уточнения итогового результата. Ядро цели отвечает на вопрос, что должно делаться системами в момент полного достижения цели.
Ядро помехи ― максимально конкретизированное свойство системы, которое необходимо устранить или модифицировать для реализации ядра подцели.
Идеальный конечный результат (ИКР) ― одно из базовых понятий ТРИЗ. Образ решения ядра цели с минимальными, в идеале – нулевыми затратами ресурсов (времени, денег, навыков, энергии, связей и прочего).
Описание алгоритма ЭФФЕКТИВНОГО РЕШЕНИЯ ПРОБЛЕМ
1) Вводные данные.
Информация о проблеме либо описание цели. Полезные факты, условия и ограничения.
2) Ядро цели.
Выявляем, что должно делаться в момент, когда мы довольны итоговым результатом.
3) Список этапов.
Создаем список самых очевидных этапов до итогового результата.
4) Ядра подцелей.
Что должно делаться во время полной реализации каждого этапа? Короткие и ясные подцели.
5) Системы.
Выписываем все системы, участвующие во всех этапах. Как правило, они одни и те же.
6) Идеальный конечный результат (ИКР).
Берем каждый этап, внутри этапа по каждой системе прописываем ИКР в формате «система сама реализует ядро подцели».
7) Список помех.
Внутри каждого этапа выявляем все помехи, которые мешают реализации ядра подцели.
8) Ядра помех.
Выделяем то свойство системы, которое создает помеху. Нам предстоит его устранить или модифицировать.
9) Первичный мозговой штурм.
Самостоятельно или в компании профессионалов пытаемся придумать путь реализации каждого ядра подцели, каждого ИКР и решение каждой помехи. Используем фантазию и личный опыт.
Используем фантазию и личный опыт.
10) Перебор ресурсов.
Перебираем наш чек-лист ресурсов, стараясь визуализировать и произносить вопросы вслух. К каждому ИКР и к каждой помехе мы перебираем все ресурсы, выписывая реалистичные варианты реализации ядра подцели.
11) Оптимизация идей.
Выписываем все изобретенные идеи, сортируем их и проверяем на реалистичность самостоятельно или в компании профессионалов. Выделяем самые простые и эффективные идеи, которые возможно реализовать с минимальными затратами в ближайшие дни, ожидая значительный результат.
12) Массовое тестирование идей.
С минимальными затратами ресурсов (денег, времени и прочего) в короткий промежуток времени массово пробуем на практике самые простые и эффективные идеи с целью вычислить, какие из них эффективнее приводят к итоговому результату.
13) Масштабирование лучших идей.
Начинаем вкладывать ресурсы именно в те идеи, которые показали максимальную эффективность при тестировании.
Универсальный чек-лист ресурсов
1. Это возможно в определенном пространстве?
Интернет, программный продукт, расположение в пространстве, страна, город, улица, помещение, место внутри помещения, место массового скопления людей…
2. Это возможно на определенных мероприятиях?
Сообщество людей, мероприятие, клуб по интересам, соревнование…
3. Это возможно в определенное время?
Время года, время суток, праздники, особые общественные события, события в жизни…
4. Каким людям будет выгодно помочь в реализации?
Отдельные люди, сообщества, знакомые, организации…
5. Это возможно, если иметь особый статус?
Быть главным в этой системе, создателем данной системы, директором, начальником, тренером, звездой, известной личностью…
6. Это возможно реализовать за деньги?
Нанять компетентного профессионала, заинтересовать щедрой оплатой участников системы…
7. Это возможно, если что-то уметь или знать?
Это возможно, если что-то уметь или знать?
Уметь что-то делать, уметь как-то воздействовать на людей, на среду, на участвующие в ядре системы…
ИСТОРИЯ
Алгоритм эффективного решения проблем (АЭРП) содержит в себе методы теории решения изобретательских задач технического характера (ТРИЗ), созданной советским инженером-изобретателем Генрихом Альтшуллером (~1946 год). В отличие от ТРИЗ, Алгоритм эффективного решения проблем (АЭРП) создавался для решения жизненных, нетехнических задач. Автором Алгоритма эффективного решения проблем (АЭРП) является Илья Владимирович Волочков. Первые варианты АЭРП и траблхакинга были придуманы и опробованы в 2012 году. Первая публикация АЭРП состоялась в 2018 году [«Дневник Реалиста: книга про деньги, отношения и смысл жизни»].
Введение в решение проблем с использованием алгоритмов поиска для начинающих
Эта статья была опубликована в рамках блога о науке о данныхОбзор
В информатике решение проблем относится к методам искусственного интеллекта, включая различные методы, такие как формирование эффективных алгоритмов, эвристика и выполнение анализа основных причин для поиска желаемых решений.
Основная задача искусственного интеллекта — решать проблемы так же, как и люди.
Примеры проблем с искусственным интеллектом
В современном быстро меняющемся цифровом мире методы искусственного интеллекта широко используются для автоматизации систем, которые могут эффективно использовать ресурсы и время. Некоторые из хорошо известных проблем, возникающих в повседневной жизни, — это игры и головоломки. Используя методы ИИ, мы можем эффективно решить эти проблемы. В этом смысле некоторые из наиболее распространенных проблем, решаемых с помощью ИИ, — это
- Задача коммивояжера
- Ханойская башня Задача
- Проблема с кувшином для воды
- Проблема N-ферзя
- Шахматы
- Судоку
- Задачи крипто-арифметики
- Магические квадраты
- Логические головоломки и так далее.
- Методы решения проблем
- Свойства алгоритмов поиска
- Типы алгоритмов поиска
- Неинформированные алгоритмы поиска
- Сравнение различных алгоритмов неинформированного поиска
- Алгоритмы информированного поиска
- Сравнение алгоритмов неинформированного и информированного поиска
В искусственном интеллекте проблемы могут решаться с помощью поисковых алгоритмов, эволюционных вычислений, представлений знаний и т. д.
д.
В этой статье я собираюсь обсудить различные методы поиска, используемые для решения проблемы.
Обычно под поиском понимается поиск нужной информации.
Процесс решения проблемы с помощью поиска состоит из следующих шагов.
- Определите проблему
- Анализ проблемы
- Идентификация возможных решений
- Выбор оптимального решения
- Реализация
Давайте обсудим некоторые важные свойства алгоритмов поиска.
Свойства алгоритмов поиска
Полнота
Алгоритм поиска считается завершенным, когда он дает решение или возвращает любое решение для данного случайного ввода.
Оптимальность
Если найденное решение является лучшим (наименьшая стоимость пути) среди всех найденных решений, то это решение называется оптимальным.
Временная сложность
Время, необходимое алгоритму для выполнения своей задачи, называется временной сложностью.
Космическая сложность
Это максимальное хранилище или память, занимаемая алгоритмом в любое время во время поиска.
Эти свойства
также используются для сравнения эффективности различных типов алгоритмов поиска.
Типы алгоритмов поиска
Теперь давайте посмотрим на типы алгоритма поиска.
Основываясь на проблемах поиска, мы можем классифицировать алгоритм поиска как
- Неинформированный поиск
- Информированный поиск
Алгоритм неинформированного поиска не имеет сведений о предметной области, таких как
как близость, расположение целевого состояния и т. д. ведет себя грубо.
Он знает только информацию о том, как обойти заданное дерево и как
найти целевое состояние. Этот алгоритм также известен как алгоритм слепого поиска
или алгоритм грубой силы.
Стратегии неосведомленного поиска бывают шести типов.
Они-
- Поиск в ширину
- Поиск в глубину
- Поиск с ограничением глубины
- Итеративное углубление поиска в глубину
- Двунаправленный поиск
- Поиск унифицированной стоимости
Давайте обсудим эти шесть стратегий одну за другой.
1. Поиск в ширинуЭто одна из самых распространенных стратегий поиска. Обычно он начинается с корневого узла и проверяет соседние узлы, а затем переходит на следующий уровень. Он использует стратегию «первым поступил — первым обслужен» (FIFO), поскольку она обеспечивает кратчайший путь к достижению решения.
BFS используется там, где данная задача очень мала и не учитывается объемная сложность.
Теперь рассмотрим следующее дерево.
Источник: Автор
Здесь давайте возьмем узел A в качестве начального состояния и узел F в качестве целевого состояния.
Алгоритм BFS начинается с начального состояния, затем переходит на следующий уровень и посещает узел, пока не достигнет целевого состояния.
В этом примере он начинает с A, затем переходит на следующий уровень и посещает B и C, а затем
перейти на следующий уровень и посетить D, E, F и G. Здесь целевое состояние определяется как F. Таким образом, обход остановится на F.
Путь обхода:
А —> Б —> С —> Г —> Е —> F
Давайте реализуем то же самое в программировании на Python.
Код Python:
Преимущества BFS
- BFS никогда не попадет в нежелательные узлы.
- Если граф имеет более одного решения, то BFS вернет оптимальное решение, обеспечивающее кратчайший путь.
Недостатки BFS
- BFS сохраняет все узлы текущего уровня и затем переходит на следующий уровень. Для хранения узлов требуется много памяти.
- BFS требуется больше времени
, чтобы достичь целевого состояния, которое находится далеко.
Поиск в глубину использует стратегию «последним пришел — первым обслужен» (LIFO), поэтому его можно реализовать с помощью стека. DFS использует поиск с возвратом. То есть он начинает с начального состояния и исследует каждый путь до наибольшей глубины, прежде чем перейти к следующему пути.
DFS будет следовать за
Корневой узел —> Левый узел —> Правый узел
Теперь рассмотрим тот же пример дерева, упомянутый выше.
Здесь он начинает с начального состояния A, затем перемещается в B, а затем переходит в D. Достигнув
D, он возвращается в B. B уже посещен, поэтому он переходит на следующую глубину E, а затем возвращается в B. .. поскольку он уже посещен, он возвращается к A. A уже посещен. Итак, он переходит в C, а затем в F. F — наше целевое состояние, и на нем он останавливается.
Путь обхода:
А —> В —> Г —> Е —> С —> F
Попробуем закодировать.график = { «А»: [«В», «С»], 'В' : ['Д', 'Е'], 'С' : ['Ф', 'Г'], 'Д': [], 'Э': [], 'Ф': [], 'Г' : [] } цель = 'F' посетили = установить () def dfs (посещено, граф, узел): если узел не посещается: печать (узел) посещенный.добавить(узел) для соседа в графе [узел]: если цель в посещении: перерыв еще: dfs(посещено, график, сосед) dfs(посещено, график, 'A') 902:30
Путь вывода следующий.
Преимущества DFS
- Занимает меньше памяти по сравнению с BFS.
- Временная сложность меньше по сравнению с BFS.
- DFS не требует дополнительных поисков.
Недостатки DFS
- DFS не всегда гарантирует решение проблемы.
- Когда DFS уходит глубоко вниз, она может попасть в бесконечный цикл.
3. Поиск с ограничением глубины
Ограничение по глубине работает аналогично поиску в глубину. Разница здесь в том, что поиск с ограничением по глубине имеет предопределенный предел, до которого он может проходить по узлам. Поиск с ограничением по глубине устраняет один из недостатков DFS, поскольку он не ведет к бесконечному пути.
Разница здесь в том, что поиск с ограничением по глубине имеет предопределенный предел, до которого он может проходить по узлам. Поиск с ограничением по глубине устраняет один из недостатков DFS, поскольку он не ведет к бесконечному пути.
DLS завершает обход, если выполняется одно из следующих условий.
Стандартный отказ
Означает, что данная задача не имеет решений.
Значение ошибки отключения
Указывает на отсутствие решения проблемы в заданном пределе.
Теперь рассмотрим тот же пример.
Возьмем A в качестве начального узла и C в качестве целевого состояния и ограничим значением 1.
Обход сначала начинается с узла A, а затем переходит на следующий уровень 1, и достигается целевое состояние C. Он останавливает обход.
Путь обхода:
А ---> С
Если мы укажем C в качестве целевого узла, а ограничение равно 0, алгоритм не вернет ни одного пути, поскольку целевой узел недоступен в пределах заданного ограничения.
Если мы зададим целевой узел как F и предел как 2, путь будет A, C, F.
Внедряем DLS.
график = {
«А»: [«В», «С»],
'В' : ['Д', 'Е'],
'С' : ['Ф', 'Г'],
'Д': [],
'Э': [],
'Ф': [],
'Г' : []
}
def DLS(начало,цель,путь,уровень,maxD):
print('nCurrent level-->',level)
path.append(начало)
если начало == цель:
print("Проверка цели прошла успешно")
Обратный путь
print('Проверка целевого узла не удалась')
если уровень==maxD:
вернуть ложь
print('nРасширение текущего узла',start)
для ребенка в графике [начало]:
если DLS(ребенок,цель,путь,уровень+1,maxD):
Обратный путь
путь.поп()
вернуть ложь
начало = 'А'
target = input('Введите узел цели:-')
maxD = int(input("Введите ограничение максимальной глубины:-"))
Распечатать()
путь = список()
res = DLS (начало, цель, путь, 0, maxD)
если (рез):
print("Доступен путь к целевому узлу")
распечатать("путь",путь)
еще:
print("Нет пути к целевому узлу в заданном пределе глубины") 902:30
Когда мы указываем C как целевой узел
и 1 как ограничение, путь будет следующим.
Преимущества DLS
- Требуется меньше памяти по сравнению с другими методами поиска.
Недостатки DLS
- DLS может не предложить оптимальное решение, если проблема имеет более одного решения.
- DLS также сталкивается с неполнотой.
4. Итеративное углубление поиска в глубину
Итеративный поиск с углублением в глубину представляет собой комбинацию поиска в глубину и поиска в ширину. IDDFS находит лучший предел глубины, постепенно добавляя предел, пока не будет достигнуто заданное целевое состояние.
Попробую объяснить это на том же дереве примеров.
Рассмотрим A как начальный узел и E как конечный узел. Пусть максимальная глубина будет 2.
Алгоритм начинает
с A и переходит на следующий уровень и ищет E. Если не найден, он переходит к
следующий уровень и находит E.
Путь обхода
А ---> Б --> Е
Попробуем это реализовать.
график = {
«А»: [«В», «С»],
'В' : ['Д', 'Е'],
'С' : ['Ф', 'Г'],
'Д': [],
'Э': [],
'Ф': [],
'Г' : []
}
путь = список()
def DFS(currentNode,destination,graph,maxDepth,curList):
curList.append (текущий узел)
если currentNode==destination:
вернуть Истина
если maxDepth<=0:
path.append(curList)
вернуть ложь
для узла в графике[currentNode]:
если DFS (узел, пункт назначения, график, maxDepth-1, curList):
вернуть Истина
еще:
curList.pop()
вернуть ложь
def iterativeDDFS(currentNode,destination,graph,maxDepth):
для я в диапазоне (maxDepth):
курлист = список()
если DFS(currentNode,destination,graph,i,curList):
вернуть Истина
вернуть ложь
если не iterativeDDFS('A','E',graph,3):
print("Путь недоступен")
еще:
print("Путь существует")
печать(путь.поп()) 902:30
Сгенерированный путь
выглядит следующим образом.
Преимущества IDDFS
- IDDFS имеет преимущества как BFS, так и DFS.

- Предлагает быстрый поиск и эффективно использует память.
Недостатки IDDFS
- Проделывает все работы
предыдущего этапа снова и снова.
5. Двунаправленный поиск
Алгоритм двунаправленного поиска полностью отличается от всех других стратегий поиска. Он выполняет два одновременных поиска, называемых поиском вперед и поиском назад, и достигает целевого состояния. Здесь граф разделен на два меньших подграфа. На одном графе поиск начинается с начального начального состояния, а на другом графе поиск начинается с целевого состояния. Когда эти два узла пересекутся, поиск будет прекращен.
Двунаправленный поиск требует, чтобы и начало, и начало цели были четко определены, а коэффициент ветвления был одинаковым в двух направлениях.
Рассмотрим приведенный ниже график.
Здесь начальное состояние — E, а целевое состояние — G. В одном подграфе поиск начинается с E, а в другом поиск начинается с G. E перейдет к B, а затем A. G перейдет к C, а затем A. Здесь оба обхода встречаются в A
E перейдет к B, а затем A. G перейдет к C, а затем A. Здесь оба обхода встречаются в A
и, следовательно, обход заканчивается.
Путь обхода
Е ---> Б ---> А ---> С ---> G
Давайте реализуем то же самое на Python.
из очереди импорта коллекций
узел класса:
def __init__(я, значение, соседи = []):
self.val = значение
self.neighbours = соседи
self.visited_right = Ложь
self.visited_left = Ложь
self.parent_right = Нет
self.parent_left = Нет
def двунаправленный_поиск (s, t):
def Extract_path (узел):
node_copy = узел
путь = []
в то время как узел:
path.append(узел.val)
узел = node.parent_right
путь.обратный()
удалить путь[-1]
в то время как node_copy:
path.append(node_copy.val)
node_copy = node_copy.parent_left
Обратный путь
q = очередь ([])
q.добавление(я)
q. append(t)
s.visited_right = Истина
t.visited_left = Истина
в то время как len(q) > 0:
n = q.поп()
если n.visited_left и n.visited_right:
вернуть extract_path(n)
для узла в n.neighbours:
если n.visited_left == True, а не node.visited_left:
узел.parent_left = п
node.visited_left = Истина
q.append(узел)
если n.visited_right == True, а не node.visited_right:
node.parent_right = п
node.visited_right = Истина
q.append(узел)
вернуть ложь
n0 = узел («А»)
n1 = узел ('B')
n2 = узел ('C')
n3 = узел ('D')
n4 = узел ('E')
n5 = узел ('F')
n6 = узел ('G')
n0.соседи = []
n1.соседи = [n0]
n2.соседи = [n0]
n3.соседи = [n1]
n4.соседи = [n1]
n5.соседей = [n2]
n6.соседей = [n2]
печать (двунаправленный_поиск (n4, n6)) 902:30
append(t)
s.visited_right = Истина
t.visited_left = Истина
в то время как len(q) > 0:
n = q.поп()
если n.visited_left и n.visited_right:
вернуть extract_path(n)
для узла в n.neighbours:
если n.visited_left == True, а не node.visited_left:
узел.parent_left = п
node.visited_left = Истина
q.append(узел)
если n.visited_right == True, а не node.visited_right:
node.parent_right = п
node.visited_right = Истина
q.append(узел)
вернуть ложь
n0 = узел («А»)
n1 = узел ('B')
n2 = узел ('C')
n3 = узел ('D')
n4 = узел ('E')
n5 = узел ('F')
n6 = узел ('G')
n0.соседи = []
n1.соседи = [n0]
n2.соседи = [n0]
n3.соседи = [n1]
n4.соседи = [n1]
n5.соседей = [n2]
n6.соседей = [n2]
печать (двунаправленный_поиск (n4, n6)) 902:30
Путь создается
следующим образом.
Преимущества двунаправленного поиска
- Этот алгоритм быстро просматривает граф.

- Для выполнения действия требуется меньше памяти.
Недостатки двунаправленного поиска
- Целевое состояние должно быть задано заранее.
- График довольно
трудно реализовать.
6. Поиск единой стоимости
Поиск по единой стоимости считается лучшим алгоритмом поиска взвешенного графа или графа с затратами. Он ищет на графике, отдавая максимальный приоритет наименьшей совокупной стоимости. Поиск по единой стоимости может быть реализован с использованием приоритетной очереди.
Рассмотрим приведенный ниже график
, где каждый узел имеет предопределенную стоимость.
Здесь S — начальный узел, а G — конечный узел.
Из S, G можно добраться следующими способами.
С, А, Е, Ж, З -> 19
С, Б, Е, Ж, З -> 18
С, Б, Г, Ж, З -> 19
С, С, Г, Ж, З -> 23
Здесь путь с наименьшей стоимостью S, B, E, F, G.
Давайте реализуем UCS на Python.
график=[['S','A',6],
['С','Б',5],
['С','С',10],
['А','Е',6],
['В','Е',6],
['В','Д',7],
['С','Д',6],
['Э','Ф',6],
['Д','Ж',6],
['Ф','Г',1]]
темп = []
темп1 = []
для i на графике:
temp.append (я [0])
temp1.append (я [1])
узлы = набор (temp).union (набор (temp1))
def UCS(график, стоимость, открытая, закрытая, cur_node):
если cur_node открыт:
открыть.удалить(cur_node)
закрытый.добавить (cur_node)
для i на графике:
if(i[0] == cur_node и cost[i[0]]+i[2] < cost[i[1]]):
открыть. добавить (я [1])
затраты[i[1]] = затраты[i[0]]+i[2]
путь[i[1]] = путь[i[0]] + ' -> ' + i[1]
затраты[cur_node] = 999999
small = min(стоимость, ключ=costs.get)
если маленький не в закрытом:
UCS(график, затраты, открытый, закрытый, малый)
затраты = дикт()
temp_cost = дикт()
путь = дикт()
для я в узлах:
затраты [я] = 999999
путь[я] = ''
открыть = установить ()
закрыто = установить ()
start_node = input("Войдите в начальное состояние:")
open. add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
UCS(график, стоимость, открытая, закрытая, start_node)
target_node = input("Введите состояние цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 902:30
add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
UCS(график, стоимость, открытая, закрытая, start_node)
target_node = input("Введите состояние цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 902:30
Создан оптимальный выходной путь
.
Преимущества UCS
- Этот алгоритм оптимален, так как выбор путей основан на наименьшей стоимости.
Недостатки UCS
- Алгоритм
не учитывает, сколько шагов нужно пройти, чтобы достичь самого нижнего пути. Это также может привести к
бесконечному циклу.
Сравнение различных алгоритмов неинформированного поиска 9(д/2))
Все дело в неосведомленных алгоритмах поиска.
Давайте рассмотрим алгоритмы информированного поиска.
Алгоритмы информированного поиска
Алгоритм информированного поиска также называется эвристическим поиском или направленным поиском. В отличие от алгоритмов неинформированного поиска, алгоритмы информированного поиска требуют таких деталей, как расстояние до цели, шаги для достижения цели, стоимость путей, что делает этот алгоритм более эффективным.
Здесь целевое состояние может быть достигнуто с помощью эвристической функции.
Эвристическая функция используется для достижения целевого состояния с наименьшими возможными затратами. Эта функция оценивает, насколько состояние близко к цели.
Давайте обсудим некоторые стратегии информированного поиска.
1. Жадный алгоритм поиска лучшего первого
Жадный поиск наилучших результатов использует свойства как поиска в глубину, так и поиска в ширину. Жадный поиск по первому наилучшему обходит узел, выбирая путь, который кажется лучшим в данный момент. Ближайший путь выбирается с помощью эвристической функции.
Ближайший путь выбирается с помощью эвристической функции.
Рассмотрим приведенный ниже график
с эвристическими значениями.
Здесь A — начальный узел, а H — целевой узел.
Жадный поиск наилучших результатов сначала начинается с A, а затем исследуются следующие соседние B и C. Здесь эвристика B равна 12, а C равна 4. Лучший путь на данный момент — это C, и, следовательно, он ведет к C. Из C , он исследует соседей F и G. эвристика F равна 8, а G равна 2. Следовательно, он переходит к G. Из G он переходит к H, эвристика которого равна 0, что также является нашим целевым состоянием.
Путь обхода
А ---> С ---> Г ---> Н
Давайте попробуем это с Python.
график = {
'А': [('В',12), ('С',4)],
'В': [('Д',7), ('Е',3)],
'С': [('F',8), ('G',2)],
'Д': [],
'Е': [('Ч', 0)],
'Ф': [('Ч', 0)],
'Г': [('Ч',0)]
}
def bfs (начало, цель, график, очередь = [], посещено = []):
если запуск не в посещении:
печать (начало)
посещенный . append (начало)
очередь=очередь+[x для x в графике[начало], если x[0][0] не в посещении]
queue.sort (ключ = лямбда х: х [1])
если очередь[0][0]==цель:
печать (очередь [0] [0])
еще:
обработка=очередь[0]
очередь.удалить(обработка)
bfs(обработка[0], цель, график, очередь, посещено)
bfs('A', 'H', график) 902:30
append (начало)
очередь=очередь+[x для x в графике[начало], если x[0][0] не в посещении]
queue.sort (ключ = лямбда х: х [1])
если очередь[0][0]==цель:
печать (очередь [0] [0])
еще:
обработка=очередь[0]
очередь.удалить(обработка)
bfs(обработка[0], цель, график, очередь, посещено)
bfs('A', 'H', график) 902:30
Генерируется выходной путь с
наименьшей стоимостью.
Временная сложность жадного поиска наилучших результатов равна O(b m ) в
наихудших случаях.
Преимущества жадного поиска наилучших результатов
- Жадный поиск наилучших результатов более эффективен по сравнению с поиском в ширину и поиском в глубину.
Недостатки жадного поиска наилучших результатов
- В наихудшем сценарии жадный алгоритм поиска наилучших результатов может вести себя как неуправляемая DFS.
- Существуют некоторые возможности для жадного алгоритма поиска лучшего первым попасть в бесконечный цикл.

- Алгоритм
не является оптимальным.
Далее давайте обсудим другой алгоритм информированного поиска, называемый алгоритмом поиска A*.
2. Алгоритм поиска A*
Алгоритм поиска A* представляет собой комбинацию как поиска с равномерной стоимостью, так и жадных алгоритмов поиска наилучшего первого. Он использует преимущества обоих с лучшим использованием памяти. Он использует эвристическую функцию для поиска кратчайшего пути. Алгоритм поиска A* использует сумму стоимости и эвристики узла, чтобы найти наилучший путь.
Рассмотрим следующий график
со следующими эвристическими значениями.
Пусть A — начальный узел, а H — конечный узел.
Сначала алгоритм начнет с A. От A он может перейти к B, C, H.
Обратите внимание на то, что поиск A* использует сумму стоимости пути и значения эвристики для определения пути.
Здесь, от A до B, сумма стоимости и эвристики равна 1 + 3 = 4.
От А до С 2 + 4 = 6.
От А до Н это 7 + 0 = 7,
Здесь наименьшая стоимость равна 4, и выбран путь от A до B. Остальные пути будут приостановлены.
Теперь из B можно попасть в D или E.
От A до B и D стоимость 1 + 4 + 2 = 7.
От A до B и E 1 + 6 + 6 = 13.
Наименьшая стоимость — 7. Выбирается путь от A до B и D и сравнивается с другими путями, которые находятся в режиме ожидания.
Здесь путь от A до C дешевле. То есть 6.
Таким образом, выбран путь от A до C, а остальные пути сохранены.
Из C теперь можно перейти к F или G.
От A до C и F стоимость 2 + 3 + 3 = 8.
От A до C и G стоимость 2 + 2 + 1 = 5.
Самая низкая стоимость — 5, что также меньше, чем у других путей, которые находятся в режиме ожидания. Следовательно, путь от A до G выбран.
Из G он может перейти в H, стоимость которого равна 2 + 2 + 2 + 0 = 6.
Здесь 6 меньше стоимости других путей, которые приостановлены.
Кроме того, H является нашим целевым состоянием. Здесь алгоритм завершится.
Путь обхода
А ---> С ---> Г ---> Н
Давайте попробуем это на Python.
график=[['А','В',1,3],
['А','С',2,4],
['А','Ч',7,0],
['В','Д',4,2],
['В','Е',6,6],
['С','F',3,3],
['С','Г',2,1],
['Д','Е',7,6],
['Д','Ч',5,0],
['F','H',1,0],
['Г','Ч',2, 0]]
темп = []
темп1 = []
для i на графике:
temp.append (я [0])
temp1.append (я [1])
узлы = набор (temp).union (набор (temp1))
def A_star (график, затраты, открытие, закрытие, cur_node):
если cur_node открыт:
открыть.удалить(cur_node)
закрытый.добавить (cur_node)
для i на графике:
if(i[0] == cur_node and cost[i[0]]+i[2]+i[3] < cost[i[1]]):
открыть. добавить (я [1])
затраты[i[1]] = затраты[i[0]]+i[2]+i[3]
путь[i[1]] = путь[i[0]] + ' -> ' + i[1]
затраты[cur_node] = 999999
small = min(стоимость, ключ=costs. get)
если маленький не в закрытом:
A_star(график, стоимость, открытая, закрытая, малая)
затраты = дикт()
temp_cost = дикт()
путь = дикт()
для я в узлах:
затраты [я] = 999999
путь[я] = ''
открыть = установить ()
закрыто = установить ()
start_node = input("Введите начальный узел:")
open.add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
A_star(график, затраты, открытые, закрытые, start_node)
target_node = input("Введите узел цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 9г) где b — коэффициент ветвления.
get)
если маленький не в закрытом:
A_star(график, стоимость, открытая, закрытая, малая)
затраты = дикт()
temp_cost = дикт()
путь = дикт()
для я в узлах:
затраты [я] = 999999
путь[я] = ''
открыть = установить ()
закрыто = установить ()
start_node = input("Введите начальный узел:")
open.add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
A_star(график, затраты, открытые, закрытые, start_node)
target_node = input("Введите узел цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 9г) где b — коэффициент ветвления.
Преимущества алгоритма поиска A*
- Этот алгоритм является лучшим по сравнению с другими алгоритмами.
- Этот алгоритм может быть использован для решения очень сложных задач и является оптимальным.
Недостатки алгоритма поиска A*
- Поиск A* основан на эвристике и стоимости. Он может не дать кратчайшего пути.
- Использование памяти больше, так как все узлы хранятся в памяти.

Теперь давайте сравним неинформированные и информированные стратегии поиска.
Сравнение алгоритмов неинформированного и информированного поиска
Неинформированный поиск также известен как слепой поиск, тогда как информированный поиск также называется эвристическим поиском. Поиск в униформе не требует много информации. Для информированного поиска требуются детали, относящиеся к предметной области. По сравнению с неинформированным поиском стратегии информированного поиска более эффективны, а временная сложность стратегий неинформированного поиска больше. Информированный поиск решает проблему лучше, чем слепой поиск.
Конец Примечания Алгоритмы поиска
используются в играх, хранимых базах данных, виртуальных пространствах поиска, квантовых компьютерах и т. д. В этой статье мы обсудили некоторые важные стратегии поиска и то, как их использовать для решения проблем в AI
, и это еще не конец. Существует несколько алгоритмов решения любой задачи. В настоящее время искусственный интеллект быстро развивается и применяется для решения многих реальных проблем. Продолжай учиться! Продолжай практиковаться!
Существует несколько алгоритмов решения любой задачи. В настоящее время искусственный интеллект быстро развивается и применяется для решения многих реальных проблем. Продолжай учиться! Продолжай практиковаться!
Медиафайлы, показанные в этой статье, не принадлежат Analytics Vidhya и используются по усмотрению Автора.
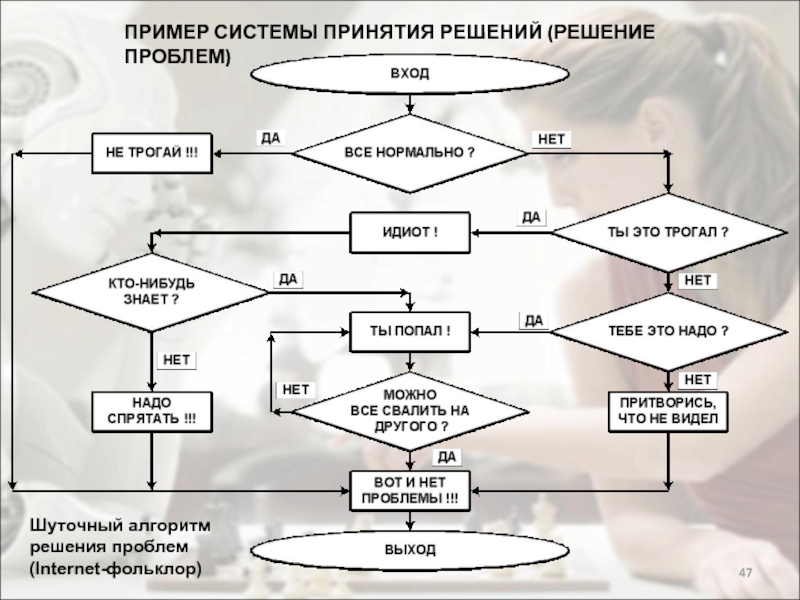
Стратегии решения проблем с алгоритмами — Сообщество разработчиков
Головоломки с алгоритмами — это, к сожалению, распространенный способ отсеять кандидатов в процессе подачи заявок. Однако, когда вы не беспокоитесь о поиске работы, это на самом деле очень весело, как кроссворды для программистов.
Их решение создает уникальные проблемы, с которыми вы не столкнетесь при запуске приложения «Еще одно сырое» и знакомит вас с концепциями, с которыми вы, возможно, еще не знакомы. Практика алгоритмических задач улучшит ваши более широкие способности решения проблем, а также укрепит процесс решения проблем, который будет более полезным в целом.
Как и в случае с другими типами головоломок, существуют стратегии, которые дают вам раннее понимание проблемы и способ разбить ее на более мелкие, более доступные фрагменты. В настоящей головоломке вы можете рассортировать кусочки по согласованным группам схожих цветов или характеристик, найти очевидные совпадения и расти дальше. С сапером вы можете начать со случайного щелчка, а затем перемещаться по открытым краям, отмечая очевидные мины и обнажая очевидные чистые области, щелкая случайным образом еще раз только тогда, когда вы исчерпали все возможности.
Несмотря на то, что существуют стратегии для работы с похожими алгоритмами, я бы порекомендовал вам начать с более широкой стратегии решения проблем, которую вы принимаете как общую привычку, а не только при работе с LeetCode в качестве подготовки к собеседованию.
Вместо того, чтобы углубляться в проблему, подойдите к проблеме поэтапно:
Подумайте:
- Проанализируйте проблему
- Переформулируйте проблему
- Запишите примеры ввода и вывода
- Разбейте проблему на составные части
- Обрисовать решение в псевдокоде
- Пройдитесь по данным вашего примера с вашим псевдокодом
Выполнить
- Закодировать
- Проверьте свое решение на своих примерах
- Рефакторинг
(Если вы знакомы с этим подходом, перейдите к шаблонам алгоритмов)
Проанализируйте проблему
Возможно, вас осенило, когда вы впервые увидели проблему. Как правило, это ваш ум, соединяющийся с каким-то предыдущим опытом. Держитесь за это понимание! Тем не менее, вы все равно должны потратить некоторое время на изучение проблемы, особенно на то, как ваше понимание отличается от фактического вопроса.
Как правило, это ваш ум, соединяющийся с каким-то предыдущим опытом. Держитесь за это понимание! Тем не менее, вы все равно должны потратить некоторое время на изучение проблемы, особенно на то, как ваше понимание отличается от фактического вопроса.
Любая хорошо написанная головоломка содержит компоненты, необходимые для решения задачи, содержащейся в одном-двух предложениях. Однако то, что вы читаете задачу, не означает, что вы ее понимаете. И если вы не понимаете проблемы, вы будете бесцельно спотыкаться или решать то, что, как вы предполагали, было проблемой.
Найдите ключевые слова, которые определяют форму задачи.
Определите ввод.
Определите желаемый результат.
Определите критически важные ключевые слова и фразы.
Например, LeetCode #26
Учитывая [отсортированный] [массив] nums, [удалить дубликаты] [на месте], чтобы каждый элемент появлялся только один раз, и [возвратить новую длину].
Не выделяйте дополнительное пространство для другого массива, это необходимо сделать, изменив входной массив на месте с [O(1) дополнительной памяти].

Ввод:
- массив. Итак, мы знаем, что, вероятно, собираемся сделать какую-то итерацию.
- массив чисел. Это больше подразумевается, чем конкретно указано, и на самом деле не так важно, как мы можем использовать тот же набор условных выражений.
Возврат:
- длина измененного массива
- побочный эффект: модифицированный массив
Критические слова и фразы:
- отсортировано: повторяющиеся элементы будут рядом друг с другом
- удалить... дубликаты
- на месте: сам массив должен быть деструктивно изменен. Это ограничение определяет, какие методы массива мы можем использовать.
- Дополнительная память O(1): мы ограничены пространственной сложностью O(1), что позволяет нам определять переменные, но не создавать копию массива.
Переформулируйте проблему
Теперь, своими словами, перефразируйте это так, чтобы оно имело для нас смысл. Если вы находитесь на собеседовании, вы можете пересказать интервьюеру, как для того, чтобы запомнить его, так и для того, чтобы убедиться, что вы правильно его услышали и поняли.
Если вы находитесь на собеседовании, вы можете пересказать интервьюеру, как для того, чтобы запомнить его, так и для того, чтобы убедиться, что вы правильно его услышали и поняли.
Пересчитано:
При наличии отсортированного массива чисел, переданного по ссылке, деструктивно изменить исходный массив на месте, удалив дубликаты, чтобы каждое значение появлялось только один раз. Возвращает длину измененного массива.
Запишите пример входных данных и ожидаемых результатов
Все, что мы делаем, это сопоставляем входы с выходами. Задача состоит в том, чтобы выяснить, как добраться из A в B, однако сначала нам нужно установить, что такое A и B . Даже если вам дали тест-кейсы, напишите свои. Глядя на что-то, не создается почти такого же понимания, как если бы вы делали это для себя.
Это также прекрасное время, чтобы изучить свое понимание проблемы и найти странности, которые могут сбить с толку наивное решение. Это включает в себя крайние случаи, такие как пустые входные данные, массив, заполненный дубликатами одного и того же значения, массивный набор данных и т. д. Нам не нужно беспокоиться ни о чем, кроме ограничений задачи 9.0005
Это включает в себя крайние случаи, такие как пустые входные данные, массив, заполненный дубликатами одного и того же значения, массивный набор данных и т. д. Нам не нужно беспокоиться ни о чем, кроме ограничений задачи 9.0005
Запишите не менее 3-х примеров:
[] -> [], возврат 0 [1] -> [1], вернуть 1 [1, 1, 2, 3, 4, 4, 4, 5] -> [1, 2, 3, 4, 5], вернуть 5 [1, 1, 1, 1, 1] -> [1], вернуть 1
Учитывая входные данные, достаточно ли у вас информации для сопоставления с результатом? Если вы этого не сделаете, сделайте шаг назад и продолжите изучение проблемы, прежде чем продолжить. Если вы проводите собеседование, не стесняйтесь просить разъяснений.
Ищите простой и последовательный процесс, который можно применять независимо от ценности для достижения результата. Если вы получите запутанную серию шагов и исключений, вы, вероятно, зашли слишком далеко и пропустили более простое решение.
Разбейте проблему на мелкие части
Начиная с самого простого примера, просто сведите задачу к основной головоломке и развивайте ее. В данном случае это массив из трех элементов, два из которых дублируются, например.
В данном случае это массив из трех элементов, два из которых дублируются, например. [1, 1, 2] . Сведение проблемы к такому небольшому случаю делает ее более доступной и проясняет первый шаг, который вам нужно сделать. Ваша задача состоит в том, чтобы разработать процедуру, которая решает этот простой случай и , справедливый для всех других случаев в наборе задач.
Итак, мы знаем, что нам нужно сделать пару вещей:
- Перебрать массив
- Следите за тем, где в массиве мы находимся
- Проверить соседние значения на равенство
- Деструктивно удалить все повторяющиеся значения после первого вхождения
- Получить окончательную длину массива и вернуть ее
Это относительно простой пример задачи, однако в ней скрывается подвох : многие итерационные методы плохо работают с удалением элементов из массива , в то время как вы перебираете массив, потому что значения индекса меняются. Вы можете в конечном итоге пропустить дубликат, потому что указатель увеличился над ним.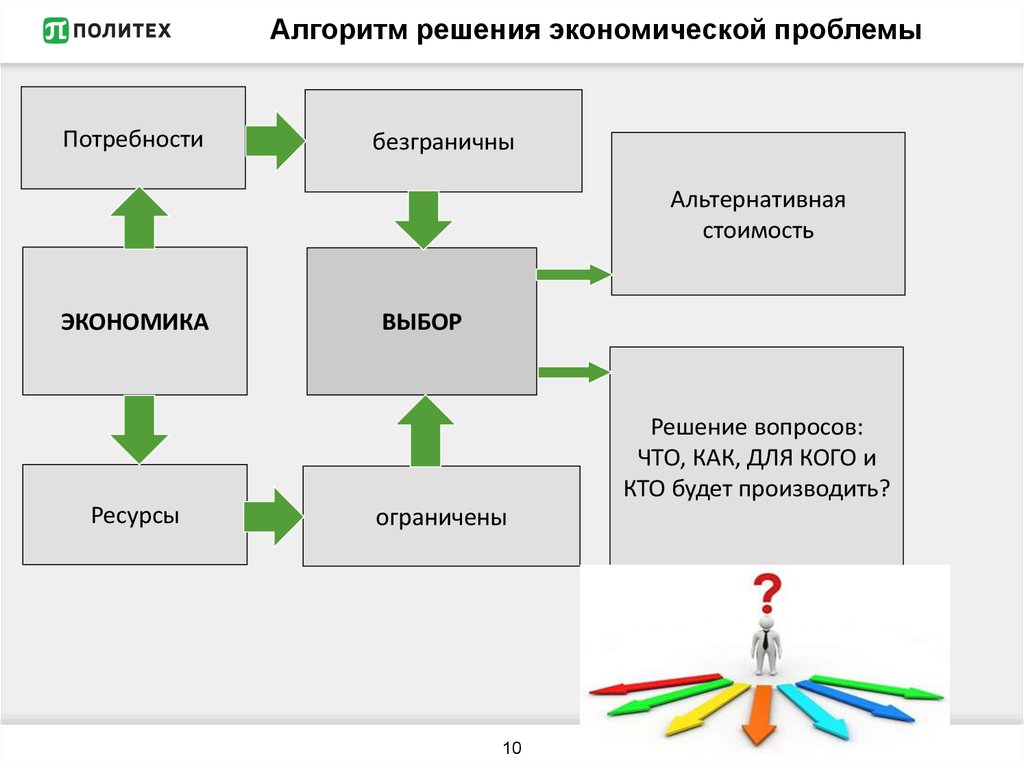
Эта ошибка указывает на то, что мы хотим использовать подход, который дает нам явное управление итерацией.
В более сложной задаче мы могли бы рассмотреть некоторые или все эти компоненты как вспомогательные функции, что позволит нам написать ясное и краткое решение, а также проверить правильность каждой из наших подчастей по отдельности.
Псевдокод решения
Если мы четко поняли проблему, определили основные задачи и, надеюсь, заметили недостатки в наших собственных предположениях и любые ошибки, мы записываем понятное для человека описание того, каким будет наш подход. Надеюсь, когда мы это сделаем, мы сможем аккуратно преобразовать его в работающий код.
То, как вы пишете псевдокод, зависит от вас. Ваши обозначения не обязательно должны быть идеально написаны и грамматически правильны. Это может быть жестовая комбинация кода и слов, предназначенная для передачи значения. Ваш псевдокод предоставит содержательную дорожную карту, к которой вы сможете вернуться, если обнаружите, что глубоко заблудились в деталях реализации, поэтому убедитесь, что вы записали достаточно, чтобы быть полезными позже.
Если вы проводите собеседование, это отличная возможность рассказать интервьюеру о ваших намерениях. И если у вас мало времени, у вас по крайней мере будет что-то на доске, демонстрирующее ваш подход к решению проблем.
Рекомендации:
- начать с сигнатуры функции:
removeDuplicates :: (массив) -> номер - при использовании интерактивной доски оставьте достаточно места для написания фактического кода
- , если вы используете IDE, пишите комментарии и храните их отдельно от кода, чтобы вы могли ссылаться на них позже.
- напишите это как серию шагов и используйте маркеры
Поскольку мы ищем дубликаты, это означает, что нам нужно выполнить сравнение. Мы можем смотреть вперед на нашу текущую позицию в массиве или мы можем смотреть назад.
// удалить дубликаты :: (массив) -> число // если массив пуст или содержит 1 элемент, вернуть длину массива и выйти // итерация по массиву // сравниваем каждый элемент со следующим элементом // // повторяем до false: // если следующий элемент совпадает с текущим элементом // удаляем следующий элемент // // переходим к следующему элементу массива // остановимся, как только будет достигнут предпоследний элемент // возвращаем длину массива
Мы начинаем с выхода, если наш массив имеет размер всего 0 или 1 элемент, отчасти потому, что эти случаи удовлетворяют условиям задачи: нет возможных дубликатов, а отчасти потому, что они сломают наш код, если мы попытаемся сравнить первое значение со вторым, которого не существует.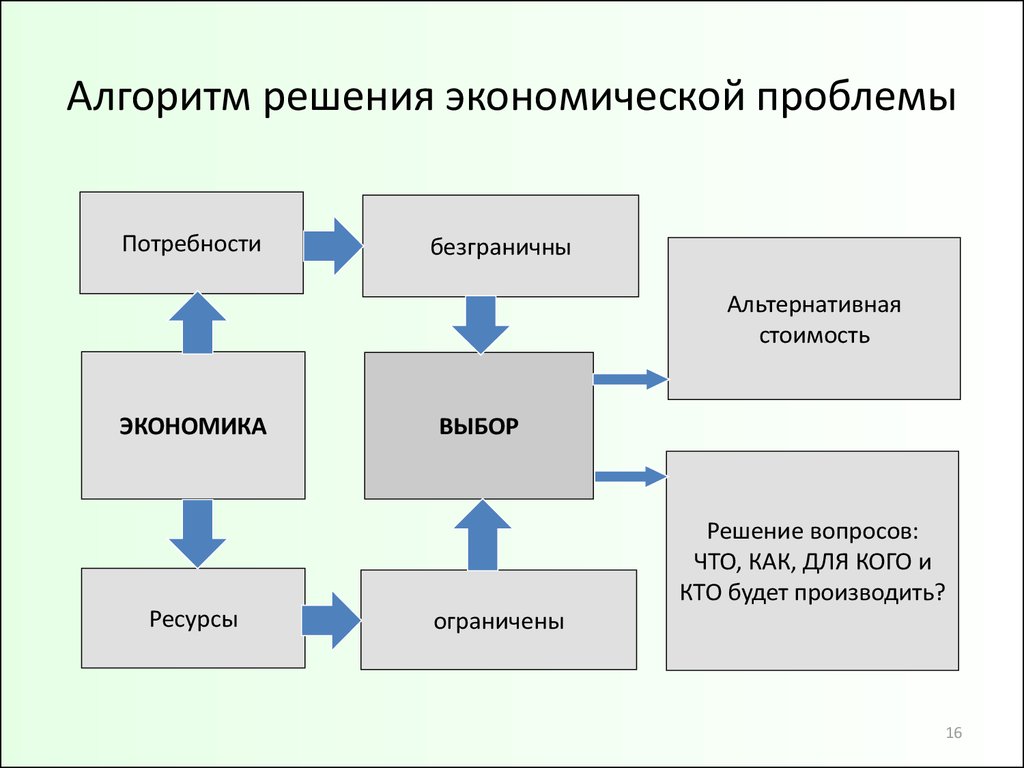
Мы также устанавливаем условие выхода из итерации, и, поскольку мы будем использовать просмотр вперед, мы обязательно остановим до того, как мы достигнем последнего элемента.
Потому что мы не перемещаем позицию указателя до после мы имели дело с любыми дубликатами, мы должны быть свободны от проблемы смещения индексов.
Пройдитесь по образцу данных
Уделите немного времени и мысленно прогоните некоторые образцы данных через наш псевдокод:
[] -> [], return 0 [1] -> [1], вернуть 1 [1, 1, 2, 3, 4, 4, 4, 5] -> [1, 2, 3, 4, 5], вернуть 5 [1, 1, 1, 1, 1] -> [1], вернуть 1
Мы что-то упустили?
Может возникнуть проблема с последним примером: [1, 1, 1, 1, 1] . Что произойдет, если мы удалим все дубликаты, а затем попытаемся перейти к следующему элементу в нашем массиве, не проверяя, есть ли они?
Мы хотим убедиться, что наше конечное условие улавливает любые изменения длины массива.
Код это
Пора резине выйти на дорогу. Здесь у вас есть все предположения, о которых вы даже не подозревали, что они вернулись, чтобы преследовать вас. Чем лучше вы смогли спланировать, тем меньше их будет.
функция удаления дубликатов (обр) {
если (arr.length < 2) вернуть arr.length
обратная длина приб.
}
Лично мне нравится сначала вводить возвращаемые значения. Таким образом, я ясно понимаю, какова моя цель, и я также зафиксировал первый случай пустых или одноэлементных массивов.
функция удаления дубликатов (обр) {
если (arr.length < 2) вернуть arr.length
for(пусть i = 0; i < arr.length; arr++) {}
обратная длина приб.
}
Да, мы используем стандартный цикл for. Я предпочитаю не использовать их, если есть более подходящий или более чистый синтаксис, но для этой конкретной проблемы нам нужна возможность контролировать нашу итерацию.
функция удаления дубликатов (обр) {
если (arr.length < 2) вернуть arr. length
for(пусть i = 0; i < arr.length; i++) {
в то время как (arr[i + 1] && arr[i] === arr[i + 1]) arr.splice(i + 1, 1)
}
обратная длина приб.
}
length
for(пусть i = 0; i < arr.length; i++) {
в то время как (arr[i + 1] && arr[i] === arr[i + 1]) arr.splice(i + 1, 1)
}
обратная длина приб.
}
И это работает из коробки, кроме:
removeDuplicates([0,0,1,1,1,2,2,3,3,4]) //> 6, должно быть 5
Оказывается, проверка существования, которую я пробрался в цикле while, разрешается как ложная, если значение массива равно 0 . Спасибо JavaScript! Так что давайте просто переработаем это очень быстро и посмотрим назад, а не вперед, что также немного очистит код:
function removeDuplicates(arr) {
если (arr.length < 2) вернуть arr.length
for(пусть i = 0; i < arr.length; i++) {
в то время как (arr[i] === arr[i - 1]) arr.splice(i, 1)
}
обратная длина приб.
}
И это проходит. Это эффективное решение для памяти, мы определили только 1 переменную, кроме ссылки на массив. И это средняя скорость, которую мы могли бы улучшить.
Но в основном это был простой пример процесса:
- Анализ
- Переформулировать
- Примеры записи
- Разберитесь с мелкими проблемами
- Контур в псевдокоде
- Шаг по псевдокоду с примерами
- Код
- Тест
- Рефакторинг
Помимо определенных структур данных и алгоритмов, которые имеют известные и довольно стандартизированные подходы, проблемы с алгоритмами, как правило, делятся на категории, которые предполагают аналогичные подходы к решению. Изучение этих подходов дает вам точку опоры в проблеме.
Изучение этих подходов дает вам точку опоры в проблеме.
Несколько указателей
Когда мы впервые учимся перебирать коллекцию, обычно массив, мы делаем это с помощью одного указателя с индексом, идущим от наименьшего значения к наибольшему. Это работает для некоторых операций и просто для рассмотрения и кода. Однако для задач, связанных со сравнением нескольких элементов, особенно тех, где важна их позиция в коллекции, поиск соответствующего значения с помощью одного указателя требует повторения массива по крайней мере один раз для каждого значения, O(n 2) операция.
Если вместо этого мы используем несколько множественных точек, мы потенциально можем сократить вычисление до операции O(n).
Существуют две общие стратегии: два указателя и скользящее окно
Два указателя
Почему бы не начать с обоих концов и не двигаться дальше? Или начните со значения или пары значений и расширяйтесь наружу. Это отличный подход для поиска самой большой последовательности в коллекции.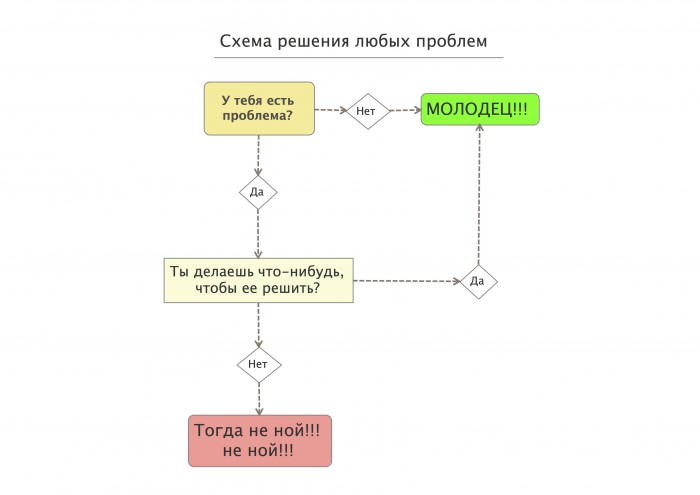
Поскольку вы работаете с двумя точками, вам необходимо определить правило, чтобы гарантировать, что они не пересекаются друг с другом.
// Временная сложность O(n)
// Пространственная сложность O(1)
функция sumZero(arr) {
пусть слева = 0;
пусть право = массив.длина - 1;
в то время как (слева < справа) {
пусть сумма = обр [слева] + обр [право];
если (сумма === 0) вернуть [обр [слева], обр [право]];
иначе если (сумма > 0) право--;
иначе осталось++;
}
}
Раздвижное окно
Вместо размещения двух точек на внешних границах мы можем пройтись по нашему массиву, последовательно перемещая два указателя параллельно. Ширина нашего окна может увеличиваться или уменьшаться в зависимости от набора задач, но оно продолжает перемещаться по коллекции, захватывая моментальный снимок любой последовательности, которая лучше всего соответствует желаемому результату.
функция maxSubarraySum(массив, n) {
если (array.length < n) n = array. length;
пусть сумма = 0;
для (пусть i = 0; i < n; i++) {
сумма = сумма + массив [i];
}
пусть maxSum = сумма;
// сдвиг окна по массиву
for (пусть я = n; я < array.length; я ++) {
сумма = сумма + массив [i] - массив [i - n];
если (сумма > maxSum) maxSum = сумма;
}
вернуть максимальную сумму;
}
length;
пусть сумма = 0;
для (пусть i = 0; i < n; i++) {
сумма = сумма + массив [i];
}
пусть maxSum = сумма;
// сдвиг окна по массиву
for (пусть я = n; я < array.length; я ++) {
сумма = сумма + массив [i] - массив [i - n];
если (сумма > maxSum) maxSum = сумма;
}
вернуть максимальную сумму;
}
Разделяй и властвуй
Разделяй и властвуй часто используется рекурсивный подход: применение одного и того же правила для разделения коллекции до тех пор, пока вы не разбьете ее на мельчайшие компоненты и не определите ответ.
Двоичный поиск и сортировка слиянием — отличные примеры рекурсивного подразделения, ведущего к решению.
O(1) Поиск: Объект/Словарь/Хэш
Хешированный ключ: Хранилища значений, называемые объектами, словарями или хэшами в зависимости от вашего языка кодирования, являются невероятно полезными инструментами для хранения информации при подсчете частоты, проверке дубликатов или дополнений ответа.


 график = {
«А»: [«В», «С»],
'В' : ['Д', 'Е'],
'С' : ['Ф', 'Г'],
'Д': [],
'Э': [],
'Ф': [],
'Г' : []
}
цель = 'F'
посетили = установить ()
def dfs (посещено, граф, узел):
если узел не посещается:
печать (узел)
посещенный.добавить(узел)
для соседа в графе [узел]:
если цель в посещении:
перерыв
еще:
dfs(посещено, график, сосед)
dfs(посещено, график, 'A') 902:30
график = {
«А»: [«В», «С»],
'В' : ['Д', 'Е'],
'С' : ['Ф', 'Г'],
'Д': [],
'Э': [],
'Ф': [],
'Г' : []
}
цель = 'F'
посетили = установить ()
def dfs (посещено, граф, узел):
если узел не посещается:
печать (узел)
посещенный.добавить(узел)
для соседа в графе [узел]:
если цель в посещении:
перерыв
еще:
dfs(посещено, график, сосед)
dfs(посещено, график, 'A') 902:30


 append(t)
s.visited_right = Истина
t.visited_left = Истина
в то время как len(q) > 0:
n = q.поп()
если n.visited_left и n.visited_right:
вернуть extract_path(n)
для узла в n.neighbours:
если n.visited_left == True, а не node.visited_left:
узел.parent_left = п
node.visited_left = Истина
q.append(узел)
если n.visited_right == True, а не node.visited_right:
node.parent_right = п
node.visited_right = Истина
q.append(узел)
вернуть ложь
n0 = узел («А»)
n1 = узел ('B')
n2 = узел ('C')
n3 = узел ('D')
n4 = узел ('E')
n5 = узел ('F')
n6 = узел ('G')
n0.соседи = []
n1.соседи = [n0]
n2.соседи = [n0]
n3.соседи = [n1]
n4.соседи = [n1]
n5.соседей = [n2]
n6.соседей = [n2]
печать (двунаправленный_поиск (n4, n6)) 902:30
append(t)
s.visited_right = Истина
t.visited_left = Истина
в то время как len(q) > 0:
n = q.поп()
если n.visited_left и n.visited_right:
вернуть extract_path(n)
для узла в n.neighbours:
если n.visited_left == True, а не node.visited_left:
узел.parent_left = п
node.visited_left = Истина
q.append(узел)
если n.visited_right == True, а не node.visited_right:
node.parent_right = п
node.visited_right = Истина
q.append(узел)
вернуть ложь
n0 = узел («А»)
n1 = узел ('B')
n2 = узел ('C')
n3 = узел ('D')
n4 = узел ('E')
n5 = узел ('F')
n6 = узел ('G')
n0.соседи = []
n1.соседи = [n0]
n2.соседи = [n0]
n3.соседи = [n1]
n4.соседи = [n1]
n5.соседей = [n2]
n6.соседей = [n2]
печать (двунаправленный_поиск (n4, n6)) 902:30

 add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
UCS(график, стоимость, открытая, закрытая, start_node)
target_node = input("Введите состояние цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 902:30
add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
UCS(график, стоимость, открытая, закрытая, start_node)
target_node = input("Введите состояние цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 902:30
 append (начало)
очередь=очередь+[x для x в графике[начало], если x[0][0] не в посещении]
queue.sort (ключ = лямбда х: х [1])
если очередь[0][0]==цель:
печать (очередь [0] [0])
еще:
обработка=очередь[0]
очередь.удалить(обработка)
bfs(обработка[0], цель, график, очередь, посещено)
bfs('A', 'H', график) 902:30
append (начало)
очередь=очередь+[x для x в графике[начало], если x[0][0] не в посещении]
queue.sort (ключ = лямбда х: х [1])
если очередь[0][0]==цель:
печать (очередь [0] [0])
еще:
обработка=очередь[0]
очередь.удалить(обработка)
bfs(обработка[0], цель, график, очередь, посещено)
bfs('A', 'H', график) 902:30
 get)
если маленький не в закрытом:
A_star(график, стоимость, открытая, закрытая, малая)
затраты = дикт()
temp_cost = дикт()
путь = дикт()
для я в узлах:
затраты [я] = 999999
путь[я] = ''
открыть = установить ()
закрыто = установить ()
start_node = input("Введите начальный узел:")
open.add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
A_star(график, затраты, открытые, закрытые, start_node)
target_node = input("Введите узел цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 9г) где b — коэффициент ветвления.
get)
если маленький не в закрытом:
A_star(график, стоимость, открытая, закрытая, малая)
затраты = дикт()
temp_cost = дикт()
путь = дикт()
для я в узлах:
затраты [я] = 999999
путь[я] = ''
открыть = установить ()
закрыто = установить ()
start_node = input("Введите начальный узел:")
open.add (начальный_узел)
путь[начальный_узел] = начальный_узел
затраты [начальный_узел] = 0
A_star(график, затраты, открытые, закрытые, start_node)
target_node = input("Введите узел цели:")
print("Путь с наименьшими затратами: ",path[goal_node]) 9г) где b — коэффициент ветвления.


 length
for(пусть i = 0; i < arr.length; i++) {
в то время как (arr[i + 1] && arr[i] === arr[i + 1]) arr.splice(i + 1, 1)
}
обратная длина приб.
}
length
for(пусть i = 0; i < arr.length; i++) {
в то время как (arr[i + 1] && arr[i] === arr[i + 1]) arr.splice(i + 1, 1)
}
обратная длина приб.
}
 length;
пусть сумма = 0;
для (пусть i = 0; i < n; i++) {
сумма = сумма + массив [i];
}
пусть maxSum = сумма;
// сдвиг окна по массиву
for (пусть я = n; я < array.length; я ++) {
сумма = сумма + массив [i] - массив [i - n];
если (сумма > maxSum) maxSum = сумма;
}
вернуть максимальную сумму;
}
length;
пусть сумма = 0;
для (пусть i = 0; i < n; i++) {
сумма = сумма + массив [i];
}
пусть maxSum = сумма;
// сдвиг окна по массиву
for (пусть я = n; я < array.length; я ++) {
сумма = сумма + массив [i] - массив [i - n];
если (сумма > maxSum) maxSum = сумма;
}
вернуть максимальную сумму;
}