Работа в термодинамике | ЕГЭ по физике
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
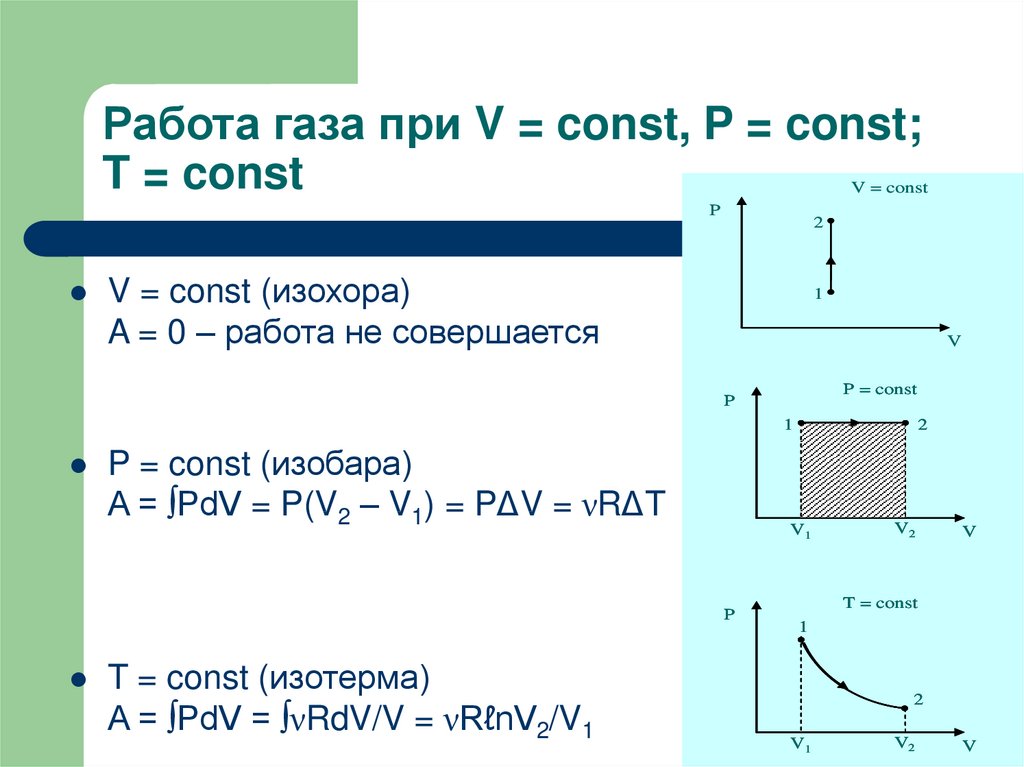
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$.
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$).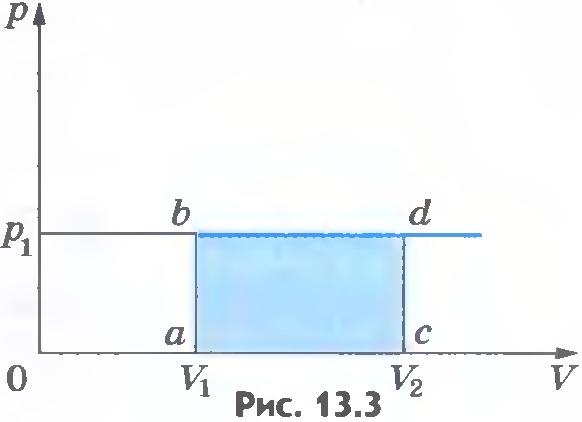
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т.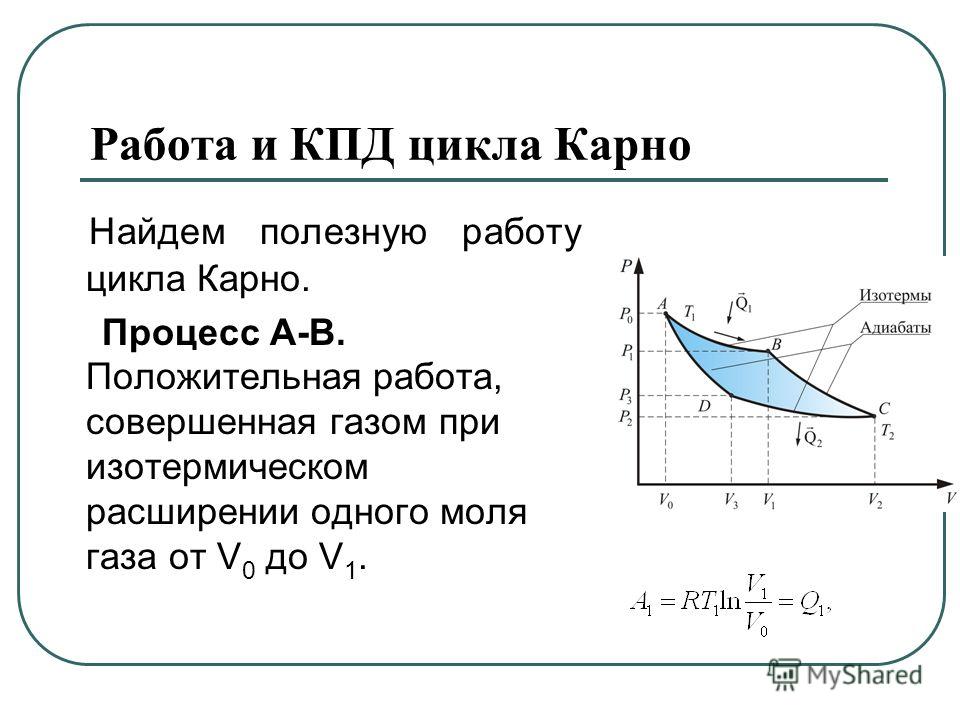 к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.

Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$).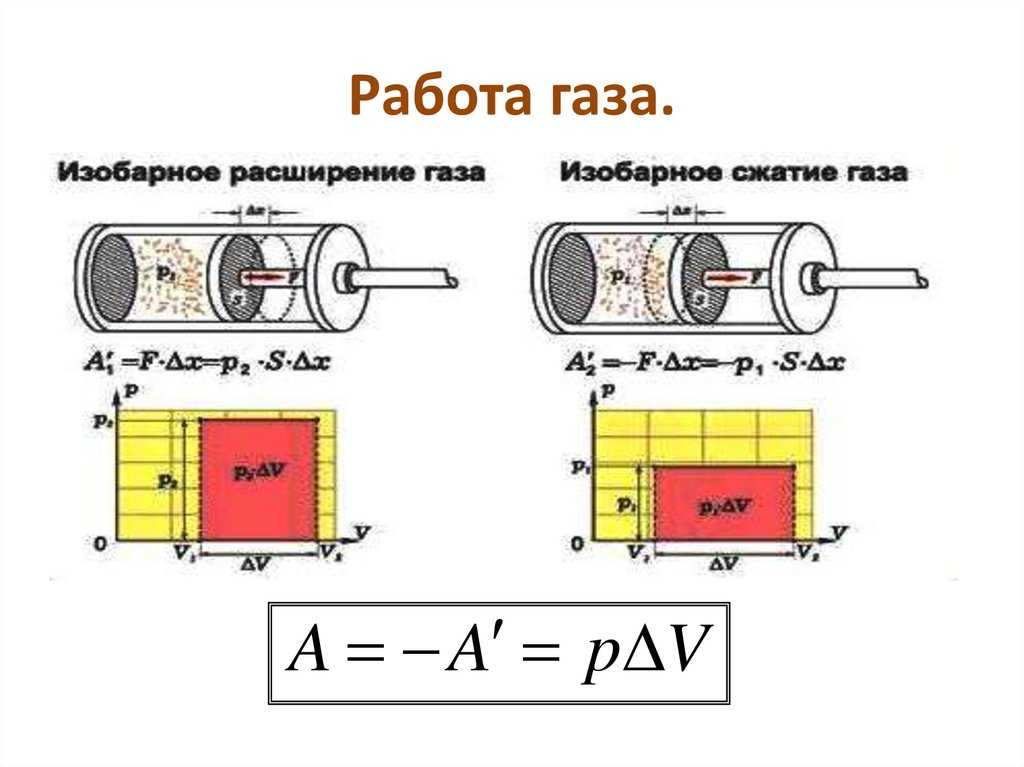 Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.
Применение первого закона термодинамики к газовым процессам
1. Изопроцессы и адиабатный процесс
Напомним, что согласно первому закону термодинамики количество теплоты Q, переданное газу, связано с изменением внутренней энергии газа ∆U и работой газа Aг соотношением
Q = ∆U + Aг. (1)
(1)
Часто требуется применять первый закон термодинамики к газовым процессам, представляющим собой последовательность изопроцессов (иногда добавляется еще адиабатный процесс).
Рассмотрим, как находить величины, фигурирующие в формуле (1), в этих процессах. Напомним, что каждая из тих величин может быть положительной, отрицательной или равной нулю.
Если график газового процесса задан не в координатах (p, V), то желательно начертить график этого же процесса в координатах (p, V), потому что с помощью этого графика легко найти работу газа. Напомним, что работа газа при расширении численно равна площади под графиком зависимости p(V), при сжатии газа – площади под тем же графиком, но взятой о знаком минус.
В большинстве задач на эту тему рассматривается однотомный идеальный газ. Напомним, что его внутренняя энергия выражается формулой
U = (3/2)νRT, (2)
где ν – количество вещества (число молей), R – универсальная газовая постоянная, T – абсолютная температура.
? 1. Чему равно изменение внутренней энергии газа в изотермическом процессе?
Из формулы (2) и уравнения состояния идеального газа
pV = νRT (3)
следует, что внутреннюю энергию одноатомного идеального газа можно выразить также формулой
U = (3/2)pV. (4)
С помощью этой формулы можно находить изменение внутренней энергии одноатомного идеального газа, если известны начальные и конечные значения давления и объема газа.
Например, если начальные значения давления и объема обозначить p1 и V1, а конечные – p2 и V2, то
∆U = (3/2) (p2V2 – p1V1). (5)
? 2. Чему равно изменение внутренней энергии при изохорном процессе, если объем газа равен V, а давление изменилось от p1 до p2?
? 3. Чему равно изменение внутренней энергии при изобарном процессе, если давление газа равно p, а объем изменился от V1 до V2?
? 4.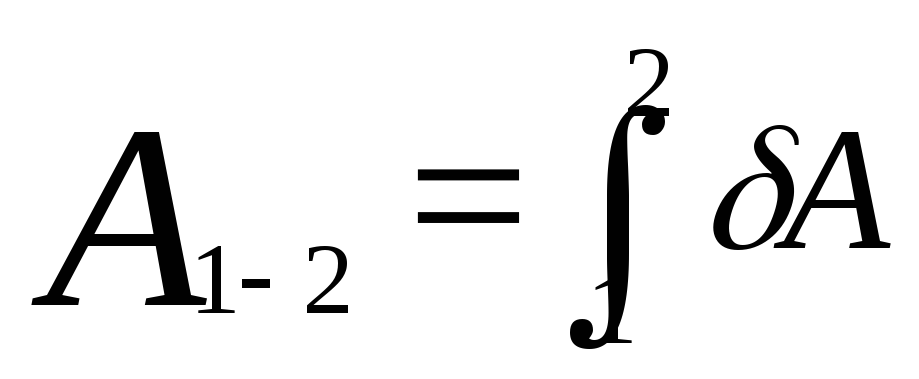 На рисунке 47.1 изображен график зависимости p(T) для ν молей одноатомного идеального газа при изохорном переходе из состояния 1 в состояние 2. Даны начальные значения давления и температуры газа p1 и T1, конечная температура T2.
На рисунке 47.1 изображен график зависимости p(T) для ν молей одноатомного идеального газа при изохорном переходе из состояния 1 в состояние 2. Даны начальные значения давления и температуры газа p1 и T1, конечная температура T2.
а) Чему равно конечное давление газа p2?
б) Чему равен объем газа V?
в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии ∆U газа?
е) Чему равно полученное газом количество теплоты Q?
? 5. На рисунке 47.2 изображен график зависимости V(T), для ν молей одноатомного идеального газа при изобарном переходе из состояния 1 в состояние 2. Даны начальные значения объема и температуры газа V1, и T1, конечная температура T2.
47.2
а) Чему равен конечный объем газа V2?
б) Чему равно давление газа p?
в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии газа?
е) Чему равно полученное газом количество теплоты Q?
? 6. Используя результаты предыдущих заданий, сравните значения количества теплоты, полученного одним и тем же количеством вещества газа в изохорном и изобарном процессе при нагревании от температуры T1 до температуры T2.
а) В каком случае количество теплоты больше? Во сколько раз больше?
б) Объясните этот результат, используя закон сохранения энергии.
Рассмотрим теперь изотермический и адиабатный процессы.
? 7. На рисунке 47.3 приведены графики зависимости p(V) для данной массы газа при изотермическом и адиабатном процессах. Какой график описывает адиабатный процесс? Поясните свой ответ.
? 8. В каком случае совершенная газом работа больше: когда он расширяется изотермически или адиабатно? Начальные объемы газа одинаковы, конечные объемы тоже одинаковы. Поясните свой ответ.
? 9. Как связаны полученное газом количество теплоты Q и работа газа Aг при изотермическом процессе?
Нахождение работы газа при изотермическом расширении выходит за рамки школьного курса физики. Но в задачах часто используется связь между Q и Aг в изотермическом процессе, выведенная вами при выполнении предыдущего задания.
? 10. В вертикальном цилиндре под поршнем массой 1 кг находится идеальный газ. При изотермическом расширении газа поршень поднялся на 5 см. Примите, что трением между поршнем и стенкой цилиндра можно пренебречь.
а) Чему равна работа газа?
б) Чему равно переданное газу количество теплоты?
? 11. Как связаны работа газа Aг и изменение его внутренней энергии ∆U при адиабатном процессе? (Напомним, что при адиабатном процессе отсутствует теплопередача, то есть Q = 0.)
Нахождение работы газа при адиабатном процессе также выходит за рамки школьного курса, но связь между Aг и ∆U в этом процессе широко используется при решении задач.
? 12. При адиабатном расширении 2 молей одноатомного идеального газа газ совершил работу 100 Дж.
а) Как изменилась при этом внутренняя энергия газа?
б) Как изменилась температура газа?
2. Циклические процессы
Циклические газовые процессы состоят из нескольких этапов, причем конечное состояние газа совпадает с начальным. Обычно рассматриваются случаи, когда этапами циклического процесса являются изопроцессы и адиабатный процесс.
Вопросы при этом ставятся, например, такие.
- На каких этапах процесса газ получает тепло, а на каких – отдает?
- Чему равно полученное газом или отданное им количество теплоты?
- Чему равно изменение внутренней энергии газа на различных этапах процесса?
- Чему равна работа газа за один цикл?
- Чему равен КПД цикла?
Для простейшего циклического процесса, состоящего из двух изохор и двух изобар, мы уже нашли ответы на эти вопросы (см. § 43). Рассмотрим теперь более сложный цикл.
На рисунке 47.4 изображен график циклического процесса, происходящего с некоторой массой одноатомного идеального газа.
На этапе 2–3 газ адиабатно расширяется, а на этапе 3–1 изотермически сжимается.
Известно, что при изобарном расширении газ совершает работу A, а при изотермическом сжатии отдает холодильнику количество теплоты Q
Проанализируем сначала этот циклический процесс качественно. По определению КПД цикла равен отношению работы, совершенной газом за один цикл, к количеству теплоты, переданному газу за этот цикл.
Работа, совершенная газом за один цикл, равна разности работы, совершенной газом при его расширении, и работы, совершенной над газом при его сжатии.
? 13. На каких этапах процесса газ совершает работу, а на каких этапах работу совершают над газом?
? 14. На каких этапах процесса газ получает тепло?
Перейдем теперь к количественному описанию. Заметим, то в подобных задачах как работу газа, так и количество теплоты удобно выражать через число молей газа и значения абсолютной температуры газа в различных состояниях газа, даже если эти значения не заданы (в таком случае они сократятся, если найдено правильное решение).
Обозначим T1, T2 и T3 значения абсолютной температуры соответственно в состояниях 1, 2, 3. Поскольку процесс 3–1 изотермический, T1 = T3.
? 15. Рассмотрим сначала изобарный процесс 1–2.
а) Выразите работу газа через давление p в этом процессе и значения объемов газа в состояниях 1 и 2.
б) Выразите эту работу через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
в) Выразите изменение внутренней энергии газа в процессе 1–2 через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
г) Выразите количество теплоты, полученное газом в процессе 1–2, через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
д) Как связано переданное газу количество теплоты с работой, совершенной газом?
? 16. Рассмотрим адиабатный процесс 2–3.
а) Каково соотношение между работой газа в этом процессе и изменением его внутренней энергии?
б) Выразите работу газа в этом процессе через число молей газа и значения абсолютной температуры в состояниях 2 и 3.
в) Найдите соотношение между работой газа в процессе 1–3 и работой газа в процессе 2–3.
? 17. Рассмотрим изотермический процесс 3–1.
а) Найдите соотношение между работой газа в этом процессе и количеством теплоты, полученным газом. Учтите, что в данном случае обе эти величины отрицательны.
б) Выразите работу Aвнеш, совершенную в этом процессе над газом, через количество теплоты Qхол, отданное газом холодильнику.
Используя результаты, полученные при выполнении предыдущих заданий, получаем, что работу Aц, совершенную газом за дин цикл, можно выразить через заданные величины:
3. Расширение газа под поршнем
Трением между поршнем и стенкой сосуда можно пренебречь
Если цилиндрический сосуд с газом расположен вертикально и трением между поршнем и стенками сосуда можно пренебречь, то при медленном нагревании процесс является изобарным. Работа газа
Aг = mgh,
где m – масса поршня, h – расстояние, на которое поднялся поршень. Используя первый закон термодинамики
Используя первый закон термодинамики
Q = ∆U + Aг,
можно связать перемещение поршня с переданным газу количеством теплоты Q и изменением его внутренней энергии ∆U. Ее можно выразить через изменение температуры ∆T и число молей газа.
? 18. Одноатомный идеальный газ находится в вертикальном цилиндрическом сосуде под поршнем массой 2 кг. Когда газу передали количество теплоты, равное 10 Дж, поршень поднялся на 5 см, а температура газа увеличилась на 2 К. Трением между поршнем и стенкой сосуда можно пренебречь. Сколько молей газа содержится в сосуде?
Учет трение между поршнем и стенкой сосуда
Типичная ошибка при решении подобных задач состоит в ом, что не учитывают силу трения покоя. Дело в том, что при увеличении давления газа под поршнем он не сдвинется с места до тех пор, пока равнодействующая приложенных к нему сил не превысит максимальную силу трения покоя, которую обычно принимают равной силе трения скольжения. Только поле этого поршень начнет двигаться, и газ начнет расширяться.
Рассмотрим пример. Пусть теперь сосуд расположен горизонтально: в таком случае вес поршня не играет роли.
? 19. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Начальное давление газа равно p0, начальное расстояние от дна сосуда до поршня равно l0, площадь поршня S (рис. 47.5).
При движении поршня на него со стороны стенки сосуда действует сила трения скольжения Fтр. Будем считать, что сосуд находится в вакууме (то есть на поршень не действует сила атмосферного давления). В начальный момент поршень находится в равновесии. Газу передают некоторое количество теплоты.
а) Какое соотношение между p0, Fтр и S следует из условия, что в начальный момент поршень находится в равновесии?
б) При каком давлении p газа поршень начнет двигаться?
в) Насколько должна увеличиться внутренняя энергия газа, чтобы поршень начал двигаться?
г) Какое количество теплоты Q надо сообщить газу, чтобы поршень начал двигаться?
д) Чему будет равно давление p газа, когда поршень будет двигаться равномерно?
е) Какую работу A совершит газ при равномерном перемещении поршня на расстояние d?
ж) Насколько увеличится при этом внутренняя энергия газа по сравнению с ее начальным значением?
з) Какое количество теплоты Q надо передать газу в начальном состоянии, чтобы поршень сдвинулся на расстояние d?
Дополнительные вопросы и задания
20. На рисунке 47.6 изображен процесс, происходящий с ν молями одноатомного идеального газа.
На рисунке 47.6 изображен процесс, происходящий с ν молями одноатомного идеального газа.
а) Начертите график этого процесса в координатах (p, V).
б) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 1–2? Учтите, что эти значения могут быть отрицательными.
в) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 2–3?
21. На рисунке 47.7 изображен график цикла, происходящего с одноатомным идеальным газом. Найдите КПД цикла.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.
 3 Законы сохранения
3 Законы сохранения - 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5 Оптика.
 СТО
СТО- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Работа газа в термодинамике. Количество теплоты. Уравнение теплового баланса. Школьный курс физики
Главная | Физика 10 класс | Работа газа в термодинамике
Глава 7.
 Основы термодинамики
Основы термодинамикиДля дальнейшего изучения тепловых процессов нужно детально исследовать, в результате каких внешних воздействий может изменяться состояние термодинамической системы (например, газа в закрытом сосуде). В этом случае существуют два различных вида воздействий, которые приводят к изменению состояния системы, т. е. к изменению её макроскопических параметров — давления р, объёма V, температуры Т. Первый из таких способов — это совершение работы (самой системой или над ней), второй способ — теплообмен (передача системе количества теплоты или отдача системой количества теплоты).
Тепловые процессы связаны с передачей и превращением энергии. Первым законом термодинамики является закон сохранения энергии, распространённый на тепловые явления. Второй закон термодинамики устанавливает направление энергетических превращений и выражает необратимость процессов в природе. Вданной главе рассмотрим первый и второй законы термодинамики, которые лежат в основе действия тепловых двигателей и машин.
§ 47. Работа газа в термодинамике. Количество теплоты. Уравнение теплового баланса
Работа газа в термодинамике.
В механике изучается движение макроскопических тел. В термодинамике движение тела как целого не рассматривается, и речь идёт о перемещении частей макроскопического тела друг относительно друга. При совершении работы изменяется объём тела и его температура, а скорость тела остаётся равной пулю. Но скорости молекул тела (например, газа) меняются, поэтому изменяется и его температура. Причина состоит в том, что при упругих соударениях молекул газа с движущимся поршнем их кинетическая энергия изменяется. Так, при движении навстречу молекулам (в случае сжатия газа) поршень во время столкновений передаёт им часть своей механической энергии, в результате чего газ нагревается. Если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Итак, при совершении работы в термодинамике меняется состояние макроскопических тел.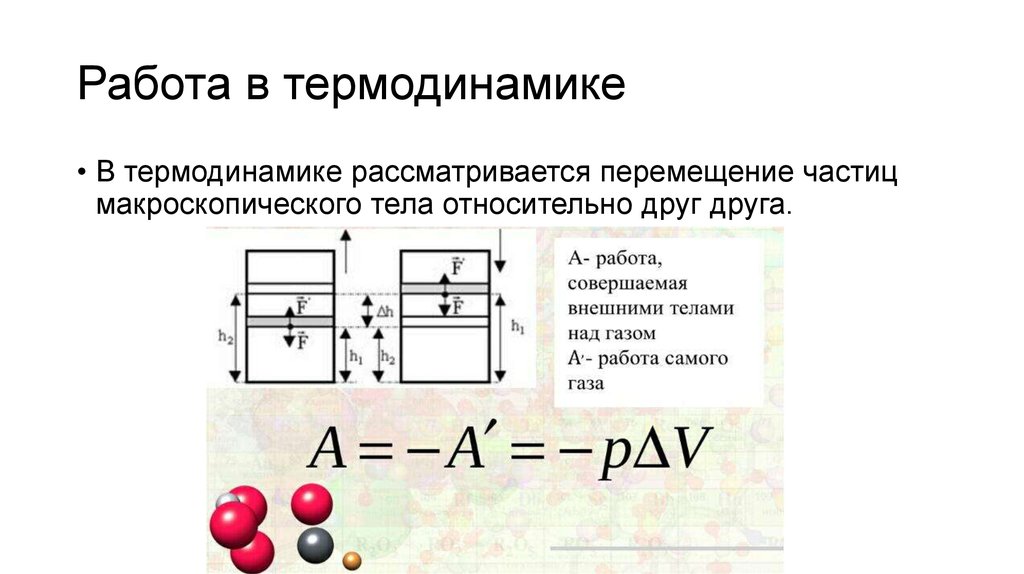
Определим работу газа, находящегося в цилиндре под поршнем, в зависимости от изменения объёма (рис. 7.1).
Рис. 7.1
Проще всего вычислить не работу силы , действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя на поршень с постоянной силой ‘. Согласно третьему закону Ньютона, = —‘.
Модуль силы, действующей со стороны газа на поршень, равен F’ = pS, где р — давление газа, a S — площадь поверхности поршня. Пусть газ расширяется, и поршень перемещается в направлении силы на малое расстояние Δh = h2 — h1 (рис. 7.1, а). Если перемещение мало, то давление газа можно считать постоянным.
Работа газа равна
Эту работу можно выразить через изменение объёма газа ΔV = V2 — V1.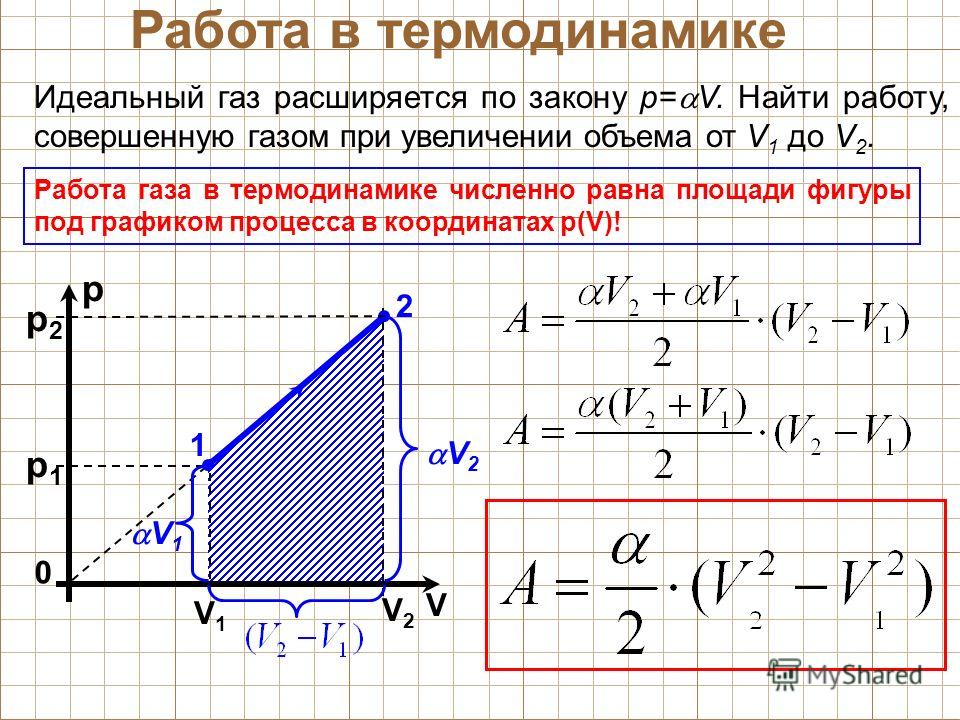 Учитывая, что начальный объём газа V1 = Sh1, а конечный — V2 = Sh2, то
Учитывая, что начальный объём газа V1 = Sh1, а конечный — V2 = Sh2, то
Если газ сжимается, то формула (1) остаётся справедливой, но в этом случае V = V2 < V1, и поэтому А’ < 0 (рис. 7.1, б). Работа А, совершаемая поршнем над газом, отличается от работы газа А’ только знаком: А = -А’ (так как сила , действующая на газ, направлена против силы ‘, а перемещение по модулю остаётся тем же самым).
Тем самым, работа внешней силы, действующей на газ, равна
Знак «минус» в этом выражении указывает, что при сжатии газа, когда ΔV = V2 — V1< 0, работа внешней силы положительна (А > 0). При этом направления силы и перемещения совпадают.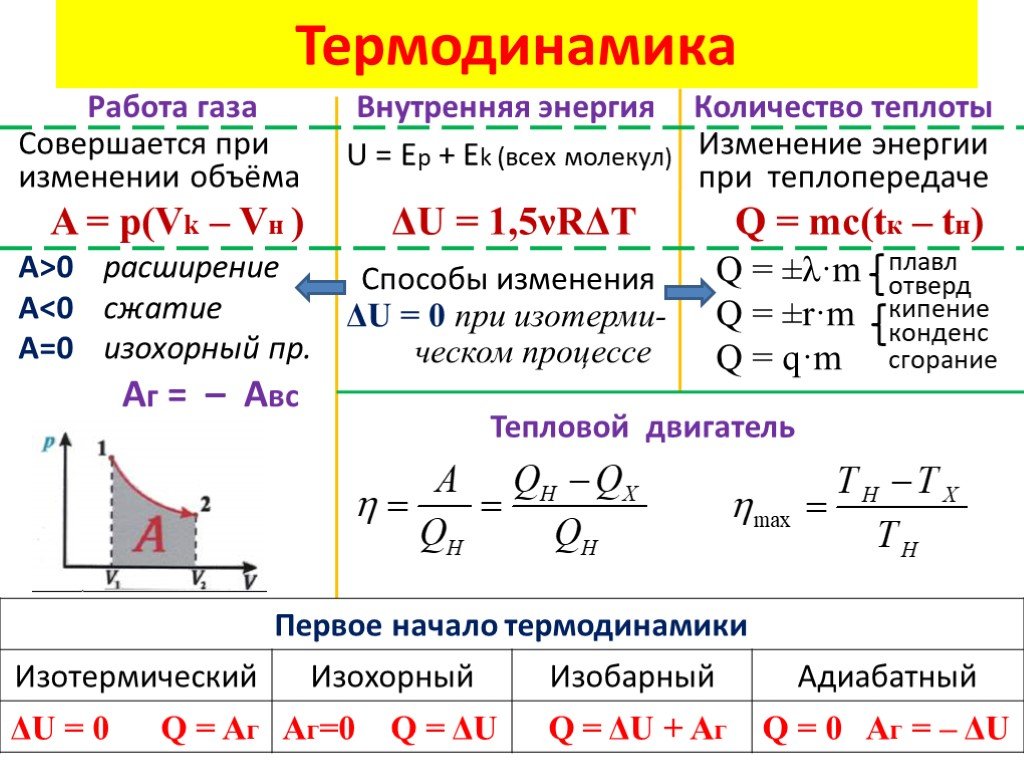 При расширении газа, наоборот, работа внешней силы отрицательна (А < 0), так как ΔV = V2 — V1> 0. В этом случае направления силы и перемещения противоположны.
При расширении газа, наоборот, работа внешней силы отрицательна (А < 0), так как ΔV = V2 — V1> 0. В этом случае направления силы и перемещения противоположны.
Выражения (1) и (2) справедливы также при малом изменении объёма любой термодинамической системы. Если процесс изобарный (р = const), то эти формулы можно применять и для больших изменений объёма.
Графический смысл работы.
Работе газа А’ для случая постоянного давления можно дать простое геометрическое истолкование. Построим график зависимости давления р газа от его объёма V (рис. 7.2).
Рис. 7.2
В этом случае площадь прямоугольника abdc, ограниченная графиком pl = const, осью V и отрезками ab и cd, равными давлению газа, численно равна работе газа А’ = p1ΔV.
В общем случае при произвольном изменении объёма газа давление не остаётся постоянным. Например, при изотермическом процессе оно убывает обратно пропорционально объёму (рис. 7.3).
Рис. 7.3
Для вычисления работы газа нужно общее изменение объёма разделить на малые части, вычислить элементарные (малые) работы, а потом все их просуммировать. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости р(V), осью V и отрезками ab и cd, равными давлениям pl и р2 в начальном и конечном состояниях.
Количество теплоты.
Изменить состояние тела можно без совершения работы, в результате нагревания. Так, состояние газа в цилиндре будет изменяться, если поршень закрепить и нагревать газ при помощи горелки (рис. 7.4).
Рис. 7.4
Объём газа при этом не меняется, но его температура и давление увеличиваются.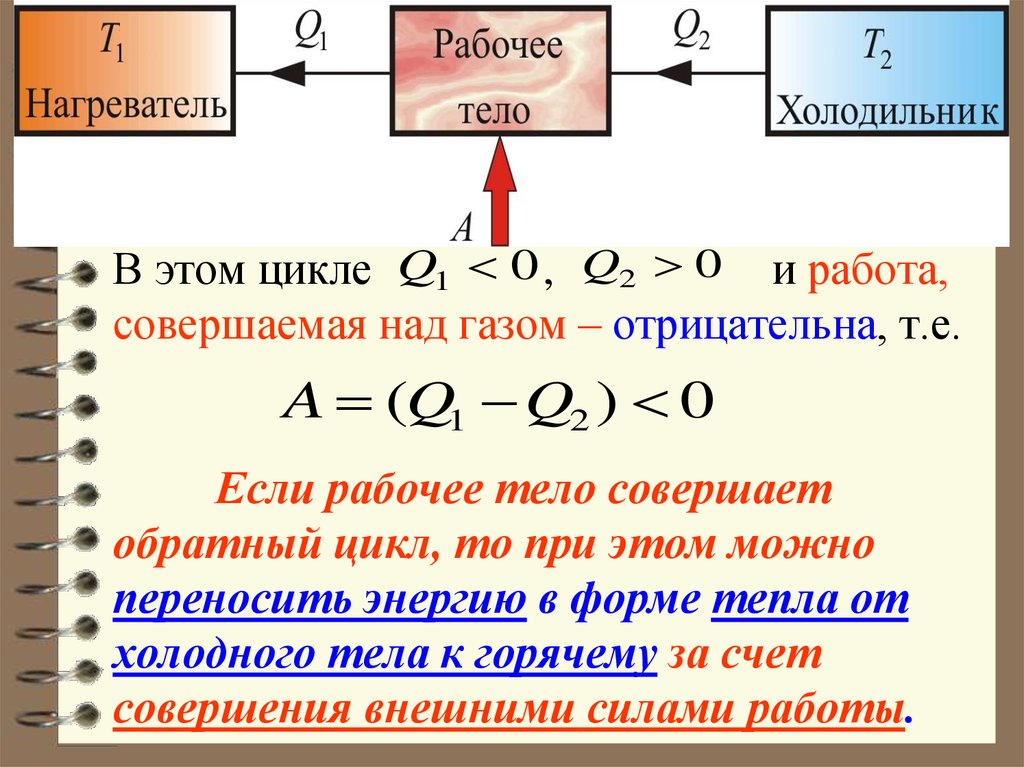 В таких случаях говорят, что системе передано некоторое количество теплоты. Нагревание тела означает увеличение скоростей теплового движения его молекул. При взаимодействии медленных молекул холодной термодинамической системы с более быстрыми молекулами горячей системы на границе систем происходит выравнивание кинетических энергий молекул. В результате теплообмена скорости молекул холодной системы увеличиваются, а горячей — уменьшаются.
В таких случаях говорят, что системе передано некоторое количество теплоты. Нагревание тела означает увеличение скоростей теплового движения его молекул. При взаимодействии медленных молекул холодной термодинамической системы с более быстрыми молекулами горячей системы на границе систем происходит выравнивание кинетических энергий молекул. В результате теплообмена скорости молекул холодной системы увеличиваются, а горячей — уменьшаются.
Исследования физических явлений опытным путём
Теплообмен между телами, изолированными от взаимодействия с окружающей средой, можно наблюдать с помощью калориметра (рис. 7.5).
Рис. 7.5
Возьмём большой тонкостенный металлический сосуд, имеющий форму стакана. Этот стакан поставим на кусочки пробки внутрь другого, большего стакана так, чтобы между стаканами оставался слой воздуха. Сверху оба сосуда закроем крышкой (рис. 7.6).
Рис. 7.6
Это несложное устройство и представляет собой калориметр. Он сконструирован так, чтобы максимально уменьшить теплообмен содержимого внутреннего стакана с внешней средой. Нальём в калориметр воду, масса которой m1 и температура t1, а затем добавим в него воды массой m2 при температуре t2. Пусть t2 > t1. В сосуде начнётся теплообмен, и спустя некоторое время установится состояние теплового равновесия — температура обеих порций воды будет одинаковой и равной t. Очевидно, t1 < t < t2.
Он сконструирован так, чтобы максимально уменьшить теплообмен содержимого внутреннего стакана с внешней средой. Нальём в калориметр воду, масса которой m1 и температура t1, а затем добавим в него воды массой m2 при температуре t2. Пусть t2 > t1. В сосуде начнётся теплообмен, и спустя некоторое время установится состояние теплового равновесия — температура обеих порций воды будет одинаковой и равной t. Очевидно, t1 < t < t2.
Изменение состояния обеих порций воды можно объяснить тем, что первая порция получила некоторое количество теплоты, а вторая — его отдала. Часть количества теплоты будет передана стенкам самого калориметра. Но если его масса во много раз меньше масс 1 и m2 порций воды, то можно пренебречь нагреванием сосуда.
В результате исследований было замечено, что для данных масс воды m1 и m2 при любых значениях начальных температур t1 и t2 выполняется равенство:
Теперь опустим в калориметр вместо второй порции воды кусок железа массой m2 при температуре t2 > t1. Спустя некоторое время в системе наступит тепловое равновесие. Однако связь между температурами и массами будет иной. В правой части появится коэффициент А, значение которого остаётся неизменным при любых массах и начальных температурах веществ:
Так как для одинаковых веществ k = 1, то этот коэффициент можно записать в виде отношения величин c2 и c1, характеризующих тепловые свойства веществ (например, железа и воды).
Обозначим изменение температуры воды через Δt1 = t — t1, а изменение температуры железа через Δt2 = t — t2 (Δt2 < 0, если t2 > t1).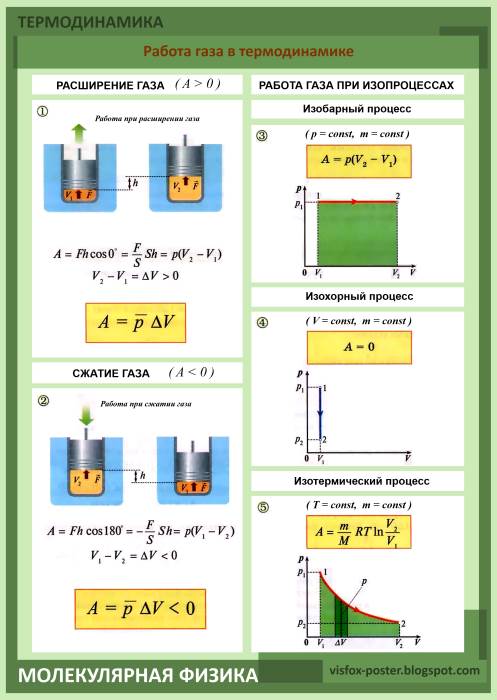 Тогда уравнение для этого случая можно записать в виде:
Тогда уравнение для этого случая можно записать в виде:
Равенство (3) имеет характер закона сохранения энергии. Сумма двух величин, одна из которых относится к первому телу, а другая — ко второму, всегда равна нулю независимо от масс тел, их температур и выбора пар тел (вода и железо были выбраны произвольно).
Итак, мы ввели новую физическую величину — количество теплоты.
Энергию, которую получает или теряет тело в процессе теплообмена, называют количеством теплоты.
В СИ количество теплоты выражают в джоулях (Дж).
В рассматриваемом примере обозначим Q1 = c1m1Δt1 — количество теплоты, полученное водой, a Q2 = c2m2Δt2 — количество теплоты, отданное железом. Тогда можно утверждать, что количество теплоты в процессе теплообмена сохраняется:
Q1 + Q2 = 0 (5)
В равенстве (5) Q1 > 0, так как Δt1 > 0 (вода нагрелась от температуры t1 до температуры t > t1), а второе слагаемое Q2 отрицательно (Q2 < 0), так как Δt1 < 0. Таким образом, полученное телом количество теплоты положительно, а отданное — отрицательно.
Таким образом, полученное телом количество теплоты положительно, а отданное — отрицательно.
Количество теплоты, отданное одним телом, равно по модулю количеству теплоты, полученному другим телом.
Уравнение (5) называют уравнением теплового баланса.
В общем случае теплообмен осуществляется между многими телами термодинамической системы, и уравнение теплового баланса запишется следующим образом:
Q1 + Q2 + Q3 + … + Qn = 0.
Здесь Q1 + Q2 + Q3 + … + Qn — количества теплоты, полученные или отданные телами системы, участвующими в теплообмене.
Удельная теплоёмкость вещества.
Если масса тела равна единице и температура меняется на единицу, то, согласно формуле (4), величина с численно равна количеству теплоты. Постоянная с численно равна количеству теплоты, которое нужно сообщить единице массы вещества, чтобы изменить его температуру на 1 °C. Эту величину называют удельной теплоёмкостью вещества. Она характеризует тепловые свойства вещества.
Эту величину называют удельной теплоёмкостью вещества. Она характеризует тепловые свойства вещества.
Единицей удельной теплоёмкости вещества в СИ является джоуль на килограмм-градус Цельсия (Дж/(кг • °C)). Так как Δt = ΔT, то эту величину также измеряют в Дж/(кг • К).
Количество теплоты, необходимое для увеличения температуры на 1 0C тела произвольной массы, называют теплоёмкостью C данного тела.
Эту величину можно определить следующим образом:
Единицей теплоёмкости в СИ является 1 Дж/К.
Теплоёмкость C тела массой m, изготовленного из вещества с удельной теплоёмкостью с, равна
C = mс.
Теплоёмкость одного моля вещества называют молярной теплоёмкостью см этого вещества.
Единицей молярной теплоёмкости в СИ является 1 Дж/(моль • °C).
Таким образом, теплоёмкость тела, содержащего ѵ моль вещества с молярной теплоёмкостью см, равна
C = ѵсм.
Вопросы:
1. Какими способами можно изменить состояние термодинамической системы?
2. Как можно вычислить работу газа в термодинамике? В чём заключается её графический смысл?
3. Какой знак будет иметь работа газа при:
а) его сжатии;
б) расширении в цилиндре?
4. Какую физическую величину называют:
а) количеством теплоты;
б) удельной теплоёмкостью вещества;
в) теплоёмкостью тела?
5. Как записывается уравнение теплового баланса?
Вопросы для обсуждения:
1. Можно ли передать телу некоторое количество теплоты, не вызывая при этом повышения его температуры?
2. На что расходуется большее количество теплоты: на нагревание чугунного горшка или воды, налитой в него, если их массы одинаковы?
Пример решения задачи
В цилиндре под поршнем находится 2 ∙ 1022 молекул идеального одноатомного газа под давлением 105 Па и при температуре 100 °C. Какую работу необходимо совершить, чтобы изобарно сжать газ до объёма, равного 0,17 л?
Какую работу необходимо совершить, чтобы изобарно сжать газ до объёма, равного 0,17 л?
Упражнения:
1. Алюминиевую и серебряную ложки одинаковой массы и температуры опустили в кипяток. Равное ли количество теплоты получат они от воды в результате теплообмена?
2. Температура воздуха в комнате объёмом 70 м3 была равна 280 К. После того как протопилась печь, температура воздуха поднялась до 296 К. Найдите работу воздуха при расширении, если атмосферное давление равно 100 кПа.
3. Идеальный газ массой 0,25 кг расширяется изобарически, совершая работу, равную 4,15 ∙ 104 Дж. Па сколько при этом нагрелся газ? Молярная масса газа равна 0,002 кг/моль.
4. Кислород массой 6,4 г нагрели на 20 °C при постоянном давлении. Найдите работу расширения газа.
5. Какое количество теплоты отдаст печь, сложенная из 300 кирпичей, при её остывании от 70 до 20 °C? Масса одного кирпича равна 5 кг, удельная теплоёмкость кирпича 0,88 кДж/(кг • °C).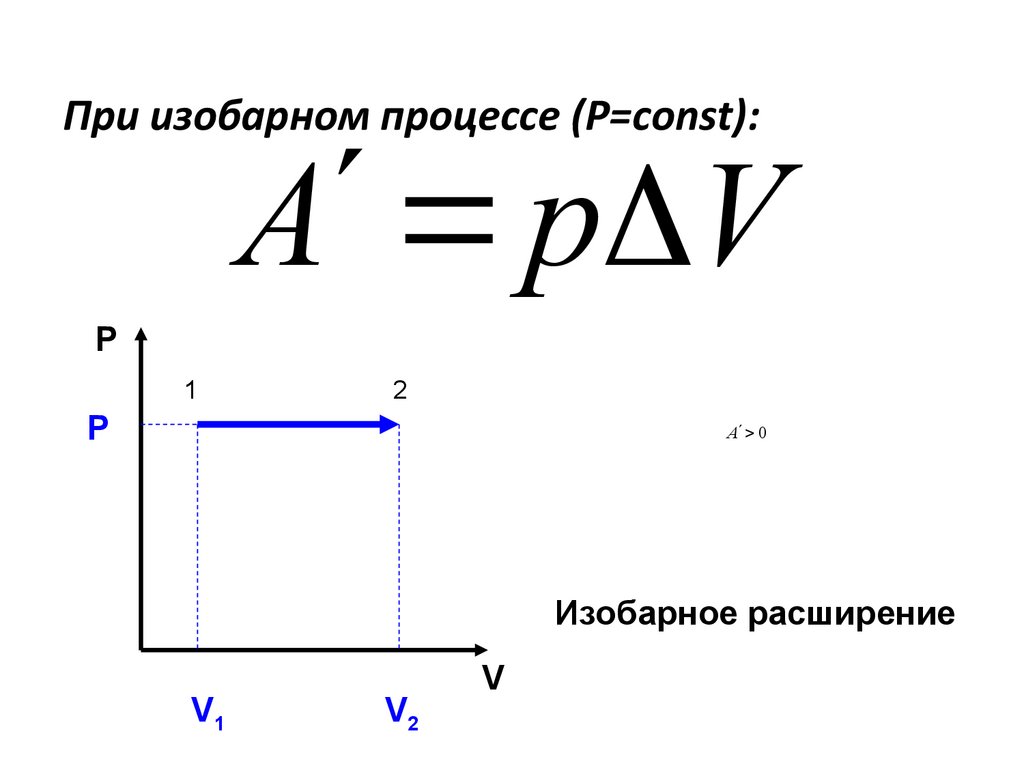
6. В латунном калориметре массой 200 г находится 400 г воды при температуре, равной 17 °C. В калориметр опустили тело из серебра массой 600 г при температуре, равной 85 °C. Определите удельную теплоёмкость серебра, если в калориметре установилась температура, равная 22 °C.
Предыдущая страницаСледующая страница
11.2. Элементарная работа. Работа идеального газа при изопроцессах
Принято считать, что если система совершает работу против действия внешних сил, то эта работа положительная.
Если внешние силы совершают работу над системой, то работа отрицательная.
Рассмотрим идеальный газ, находящийся под поршнем в цилиндре (рис. 11.6). Газ расширяется, и поршень поднимается на бесконечно малую высоту . Силу, действующую со стороны газа на поршень, находим по формуле
,
где
– давление газа на поршень;– площадь поршня. Бесконечно малую
работу, совершаемую газом, можно найти
по формуле
Бесконечно малую
работу, совершаемую газом, можно найти
по формуле
,
где – бесконечно малое изменение объёма газа. Окончательно
(11.6)
Рис. 11.6 |
Элементарной работой газа называется величина
. (11.7)
Это выражение остается справедливым для элементарной работы произвольной физически однородной и изотропной термодинамической системы в равновесном процессе.
Работа A12 термодинамической системы в равновесном
процессе перехода из начального состояния
с объёмом V1 в конечное состояние с объёмом V2 (работа в конечном процессе) вычисляется
интегрированием.
При конечном изменении объёма газа от доработа
. (11.8)
Изобразим процесс перехода системы из начального состояния 1 в конечное состояние 2, построив график зависимости P(V). Элементарная работа численно равна площади прямоугольника с длинами сторон P и dV. Работа в конечном процессе, когда объём изменяется от до, работа равна площади фигуры, ограниченной отрезкомоси абсцисс, соответствующим этому отрезку участком графика функцииP(V) и проходящими через концы отрезка параллельными оси ординат прямыми.
Рис. 11.7 | Работа – это мера изменения внутренней энергии системы в процессе совершения работы. Работа является
функцией процесса, но не является
функцией состояния. |
Работа идеального газа при изопроцессах
Вычислим работу идеального газа при изопроцессах.
I. Рассмотрим изобарический процесс (рис. 11.8).
П
Рис. 11.8
ри изобарическом процессе. Если в результате этого процесса объём газа изменился отдо, то работа газа
; (11.9)
Построим график процесса в координатах . Работаграфически выражается площадью заштрихованного прямоугольника.
II. Рассмотрим изохорический процесс (рис. 11.9). При изохорическом процессе и изменение объёма газаdV = 0 равно нулю. Следовательно, согласно формулам (11.6) и (11.9) работа газа при изохорическом процессе равна нулю.
III. Рассмотрим изотермический процесс. При изотермическом процессе и внутренняя энергия газа
. (11.10)
(11.10)
Изменение внутренней энергии , т.к..
Если в результате этого процесса объём газа изменился от до, то работа газа равна:.
Но здесь . Найдём давлениеиз уравнения Менделеева – Клапейрона:
.
Тогда
, и
.
Итак, при изотермическом процессе:
. (11.11)
Строим график процесса в координатах .
Работа графически выражается заштрихованной площадью под изотермой.
11.3. Первое начало термодинамики
Рассмотрим газ в
теплоизолированном цилиндре
(теплоизолированную термодинамическую
систему), рис.
11.11. Цилиндр
разделен жесткой теплопроводящей
перегородкой на два отсека C и D.
Объём отсека С поддерживается постоянным, над этой
частью газа не может быть совершена
работа. Объём отсека D может меняться при помощи подвижного
поршня. За счет теплопроводящей
перегородки отсеки могут обмениваться
внутренней энергией.
За счет теплопроводящей
перегородки отсеки могут обмениваться
внутренней энергией.
Если в результате совершения над системой C+D внешними силами работы , система перешла из произвольного состояния1 в произвольное состояние 2, то при этом изменилась внутренняя энергия системы. Тогда .
Тогда, изменение внутренней энергии газа в отсекеС произошло за счет теплообмена без совершения работы и равно количеству теплоты Q, полученному газом через жёсткую перегородку. Обозначим изменение внутренней энергии газа в отсекеD. Тогда получим: . Это равенство является математическим выражениемпервого начала термодинамики. Оно подразумевает, что полученное термодинамической системой количество теплоты Q равно приращению её внутренней энергии за вычетом работы над системой внешних сил.
Если переход
системы из состояние 1 в состояние 2 является равновесным, то
=
–A,
где А – работа системы против внешних сил. В таком случае
В таком случае
. (11.12)
Это выражение представляет собой интегральную форму записи первого начала термодинамики.
Равенство подразумевает, что полученное термодинамической системой в равновесном процессе количество теплоты Q идет на приращение его внутренней энергии и совершение работы над внешними телами.
Для бесконечно малого (элементарного) равновесного процесса уравнение принимает вид:
. (11.13)
Это выражение представляет собой дифференциальную форму записи первого начала термодинамики.
Первое начало термодинамики – это закон сохранения и превращения энергии. I начало термодинамики – частный случай всеобщего закона сохранения энергии: полная энергия замкнутой системы может изменяться только качественно, количественно оставаясь неизменной.
Таким образом,
первое начало термодинамики является
фундаментальным постулатом, утверждающим
собой закон сохранения энергии.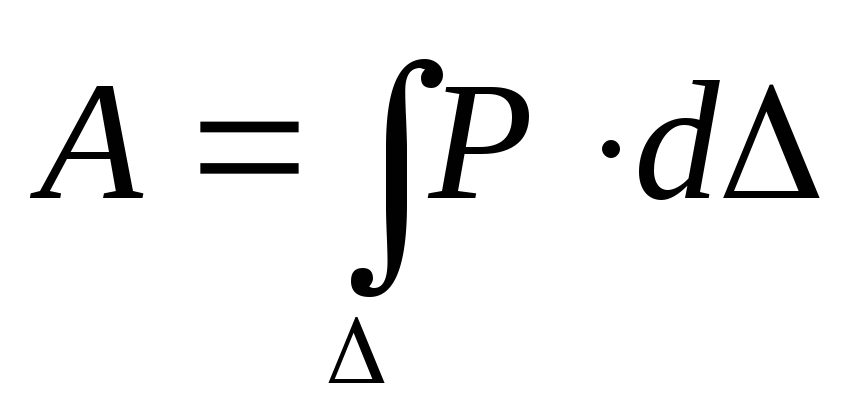 Оно
устанавливает закон взаимопревращения
теплоты, энергии и работы. За всю историю
развития науки не обнаружено опытных
фактов, которые противоречили бы этому
постулату.
Оно
устанавливает закон взаимопревращения
теплоты, энергии и работы. За всю историю
развития науки не обнаружено опытных
фактов, которые противоречили бы этому
постулату.
Дифференциальная форма записи закона подчеркивает важные свойства теплоты, энергии и работы. Обратим на это внимание.
Внутренняя энергия термодинамической системы (или тела) – это сумма всех видов энергии (энергии теплового движения атомов или молекул, потенциальная энергия их взаимодействия и т.п.), заключающихся в данной системе, за исключением энергии, которой система обладает в результате взаимодействия с другими телами. Внутреннюю энергию можно изменить двумя способами.
1. Газ находится под поршнем. Вдвигая поршень, совершаем работу. Газ сжимается и нагревается, его внутренняя энергия изменяется. Совершение работы – первый способ изменения внутренней энергии тела.
2. Но можно изменить
внутреннюю энергию тела и другим
способом, не совершая работы А,
а только подводя к телу тепло. Газ
находится под поршнем. Пусть поршень
закреплён. При подведении тепла к газу,
его внутренняя энергия меняется.
Газ
находится под поршнем. Пусть поршень
закреплён. При подведении тепла к газу,
его внутренняя энергия меняется.
Подведение некоторого количества теплоты – второй способ изменения внутренней энергии тела. Но тогда теплота и работа должны быть эквивалентными формами передачи энергии.
Работа – способ передачи энергии. В процессе работы происходит переход энергии из одного вида энергии в другой.
Теплота – тоже способ передачи энергии.
Внутренняя энергия является функцией состояния системы (или тела, если система состоит из одного тела). Это означает, чтооднозначно определяется термодинамическим состоянием тела, т.е. каждому состоянию тела соответствует одно значение.
Если тело в состоянии 1 имеет энергию
,
а в состоянии2 – энергию
,
то изменение энергиине зависит от того, каким путём совершается
переход из одного состояния в другое.
Следовательно, бесконечно малое изменениевнутренней энергии является полным
дифференциалом (11. 13).
13).
Количества теплоты и работы зависят от пути перехода системы из начального в конечное состояние, они не являются функциями состояния системы, их бесконечно малые изменения ине являются полными дифференциалами, что подчёркивается в записи этих величин в формуле (11.13).
В СИ количество теплоты, энергия и работа измеряются в джоулях (Дж).
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 22 из 28Следующая ⇒ Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A’. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = –A’. Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение. При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой: или в пределе при ΔVi → 0: В изохорном процессе (V = const) газ работы не совершает, A = 0. В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением:
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0. Первый закон термодинамики для изотермического процесса выражается соотношением Q = A. Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам. Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называютсяадиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими. Работа газа в адиабатическом процессе выражается через температуры T1 и T2 начального и конечного состояний:
М
Молярная и удельная теплоемкость газа. Молярная теплоемкость Молярная теплоемкость — теплоемкость 1 моля идеального газа. Теплоемкость идеального газа в изопроцессах Адиабатический В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть . При изменении объема температура и давление меняются, то есть . Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0. Изотермический В изотермическом процессе постоянна температура, то есть . При изменении объема газу передается (или отбирается) некоторое количество тепла. Изохорный В изохорическом процессе постоянен объем, то есть . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δA = δVP). Первое Начало Термодинамики для изохорического процесса имеет вид: А для идеального газа Таким образом, где i — число степеней свободы частиц газа. Изобарный В изобарном процессе ( ): CP=δQ/νΔT=CV+R=((i+2)/2)*R Уде́льная теплоёмкость (Удельная теплота нагревания на один градус, обозначается как c) вещества определяется как количество тепловой энергии, необходимой для повышениятемпературы одного килограмма вещества на один градус. Единицей СИ для удельной теплоёмкости является Джоуль на килограмм — Кельвин. Следовательно, удельную теплоёмкость можно рассматривать как теплоёмкость единицы массывещества. Формула расчёта удельной теплоёмкости: , где — удельная теплоёмкость, — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), — масса нагреваемого (охлаждающегося) вещества, — разность конечной и начальной температур вещества. Связь Cv и Cp : т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии одного моль газа при повышении его температуры на 1 К. Поскольку Um=(i/2)RT , то (5) Если газ нагревается при постоянном давлении, то выражение (3) можно представить в виде Учитывая, что (Um/dT) не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (4)), и дифференцируя уравнение Клапейрона — Менделеева pVm=RT (42. (6) Выражение (6) называется уравнением Майера; оно говорит о том, что Сp всегда больше СV ровно на величину молярной газовой постоянной. Это объясняется тем, чтобы осуществить нагревание газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (5), формулу (6) можно записать в виде (7) При исследовании термодинамических процессов важно знать характерное для каждого газа отношение Сp к СV : (8) Из формул (5) и (7) следует, что молярные теплоемкости зависят лишь от числа степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, которое проявляется в теплоемкости, зависит от температуры. По закону равномерного распределения энергии по степеням свободы, для комнатных температур СV = (7/2)R. Из качественной экспериментальной зависимости молярной теплоемкости СV водорода (рис. 1) следует, что СV следующим образом зависит от температуры: при низкой температуре (≈50 К) СV = (3/2)R, при комнатной — CV = (5/2)R (вместо расчетных (7/2)R) и при очень высокой — СV= (7/2)R. Это можно объяснить, сделав предположение, что при низких температурах наблюдается только поступательное движение молекул, при комнатных — добавляется их вращение, а при высоких — к данным двум видам движения добавляются еще колебания молекул.
II начало термодинамики Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Существуют несколько эквивалентных формулировок второго начала термодинамики: § Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему»[1] (такой процесс называется процессом Клаузиуса). § Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона). Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло Q1 у нагревателя, отдав Q2 холодильнику и совершив при этом работу A = Q1− Q2. После этого воспользуемся процессом Клаузиуса и вернем тепло Q2 от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен. С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Таким образом, постулаты Клаузиуса и Томсона эквивалентны. Другая формулировка второго начала термодинамики основывается на понятии энтропии: § «Энтропия изолированной системы не может уменьшаться» ( закон неубывания энтропии ). Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано. Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид[2]: Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния S = S(T,x,N), называемая энтропией, такая, что ее полный дифференциал dS = δQ / T. В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны. Ограничения С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существованиефлуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала. ⇐ Предыдущая17181920212223242526Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 2020; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Адиабатические, изотермические, изобарические и изохорные процессы
Автор Wojciech Sas, PhD кандидат
Отзыв от Bogna Szyk
Последнее обновление: 7 декабря 2021 г.
Содержание:- Что такое термодинамические процессы? Формула комбинированного газового закона
- Первый закон термодинамики
- Изохорный процесс
- Изобарический процесс
- Изотермический процесс
- Адиабатический процесс
- Пример расчета
- Цикл Карно
Калькулятор комбинированного газового закона — отличный инструмент для решения проблем, связанных с наиболее распространенными превращениями газов . Прочтите об изобарических, изохорных, изотермических и адиабатических процессах идеальных газов (газов, которые можно описать уравнением идеального газа). И как идеальные газы могут совершать работу или выделять/поглощать тепло. Проверьте точные значения для реальных газов и забудьте о термодинамических упражнениях!
И как идеальные газы могут совершать работу или выделять/поглощать тепло. Проверьте точные значения для реальных газов и забудьте о термодинамических упражнениях!
Что такое термодинамические процессы? Формула комбинированного газового закона
Идеальный газ можно описать несколькими параметрами: давлением p , объемом V , температурой T и количеством частиц n . Они соотносятся с уравнением: p * V = n * R * T , где R обозначает постоянную идеального газа и равняется 8,3144598 Дж/(моль * K) .
Во время любого процесса по крайней мере два из этих свойств изменяются , что можно представить в виде формулы комбинированного газового закона: p * V / T = k , где k — константа.
Из всех трансформаций можно выделить несколько, которые охватывают подавляющее большинство примеров из повседневной жизни, или их можно рассматривать как хорошие приближения.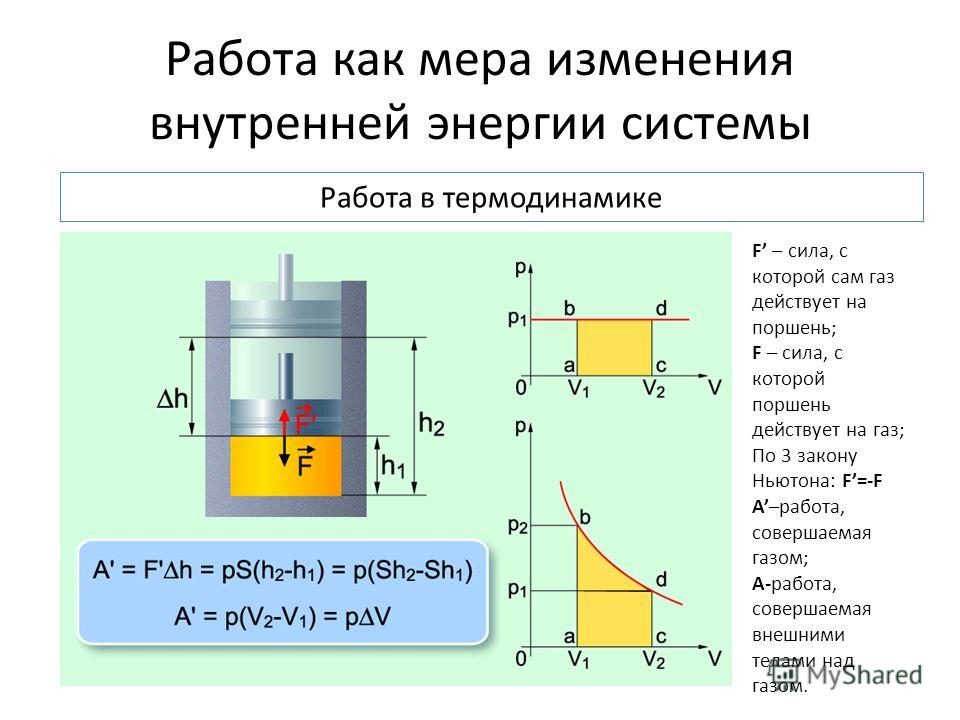 В этом калькуляторе комбинированного газового закона мы рассматриваем процессы, в которых количество частиц постоянно, поэтому мы можем представить себе газ в закрытом контейнере. Это:
В этом калькуляторе комбинированного газового закона мы рассматриваем процессы, в которых количество частиц постоянно, поэтому мы можем представить себе газ в закрытом контейнере. Это:
- изохорный процесс,
- изобарический процесс,
- изотермический процесс,
- адиабатический процесс.
Первый закон термодинамики
Внутренняя энергия U представляет собой сумму всех видов энергий, присутствующих в системе. Довольно сложно оценить точное значение внутренней энергии, но можно найти изменений тепловой энергии ΔU , которые описываются первым законом термодинамики: ΔU = Q - W , где Q обозначает тепло поглощается , а Вт равно работа, совершаемая газом . Изменение внутренней энергии пропорционально изменению температуры ΔT и типу газа по следующему уравнению: ΔU = Cv * n * ΔT , где Cv — молярная теплоемкость при постоянном объеме.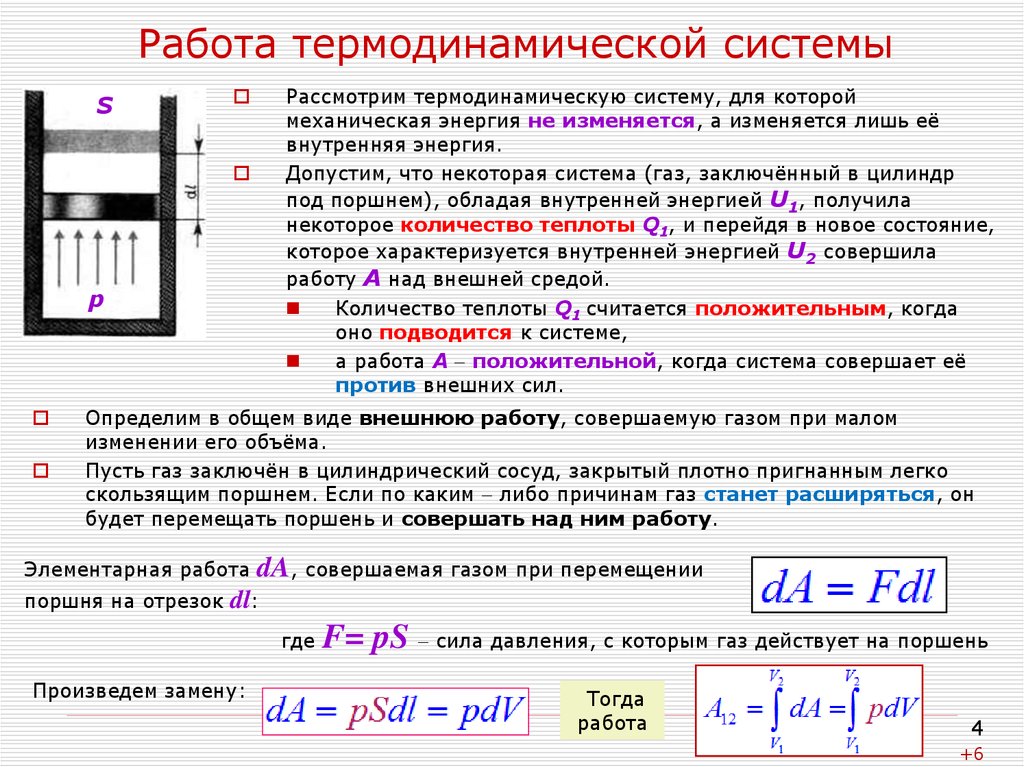 Для идеального газа принимает значения:
Для идеального газа принимает значения:
-
3/2 * Rдля одноатомного газа, -
5/2 * Rдля двухатомного газа, -
3 * Rдля газов с более сложными молекулами.
В реальных газах эти параметры отличаются от теоретических, но это уже содержится в нашем калькуляторе термодинамических процессов. Общая формула работы, совершаемой газом, выражается так: ∫p(V)dV если рассматривать давление как функцию объема . Хотя в целом это нетривиально, вы можете проверить, как формула упрощается для процессов, упомянутых ниже.
Изохорический процесс
Во время этого перехода Объем является постоянным параметром , так что начальные свойства P₁ , T₁ изменяются до P₂ , T₂ следующим образом: P₁ / T₁ / T₂ / T₂ . Неизменность объема означает, что газ не совершает никакой работы и теплота, поглощаемая газом, в точности равна изменению внутренней энергии: ΔU = Q = Cv * n * ΔT . Этот процесс можно визуализировать для газа, находящегося в жестком контейнере, но способного обмениваться теплом с окружающей средой. Закон Гей-Люссака соответствует этому термодинамическому процессу.
Этот процесс можно визуализировать для газа, находящегося в жестком контейнере, но способного обмениваться теплом с окружающей средой. Закон Гей-Люссака соответствует этому термодинамическому процессу.
Изобарический процесс
Предполагается, что давление является постоянным параметром газа во время этого перехода. Поэтому начальные параметры В₁ , T₁ преобразовать в V₂ , T₂ с помощью следующей формы формулы комбинированного газового закона: V₁ / T₁ = V₂ / T₂ . Ввиду неизменности давления формула работы, совершаемой газом, имеет вид: Вт = p * ΔV . Теплота, однако, может быть рассчитана как: Q = ΔU + W = Cv * n * ΔT + p * ΔV = Cp * n * ΔT . Cp известен как молярная теплоемкость при постоянном давлении, а для идеального газа ассоциируется с Cv , так что Cp = Cv + R . С этим переходом связан закон Шарля.
Изотермический процесс
Постоянный параметр в этом переходе составляет температуру , так что начальные свойства P₁ , V₁ изменение до P₂ , V₂ и корреляция: P₂ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ * v₁ ₁ . * В₂ . В представленном примере мы видим, что, согласно уравнению идеального газа, давление является следующей функцией объема:
* В₂ . В представленном примере мы видим, что, согласно уравнению идеального газа, давление является следующей функцией объема: p(V) = n * R * T / V = A / V , где A постоянно на протяжении всего процесса. Общее выражение для работы, совершаемой газом, можно оценить следующим образом: W = n * R * T * ln(V₂ / V₁) , где ln — натуральный логарифм данного числа. Из-за постоянства температуры начальная энергия не меняется , откуда следует равенство: Q = W . Можно сказать, что вся теплота, поглощаемая газом, превращается в совершаемую им работу, но, с другой стороны, этот переход, как известно, равен очень медленно на практике. Закон Бойля описывает термодинамические процессы такого рода.
Адиабатический процесс
При этом переходе изменяются все три параметра, но одновременно газ не обменивается теплотой с окружающей средой . Справедлива следующая формула: p₁ * V₁ γ = p₂ * V₂ γ , где γ = Cp / Cv известно как отношение теплоемкости .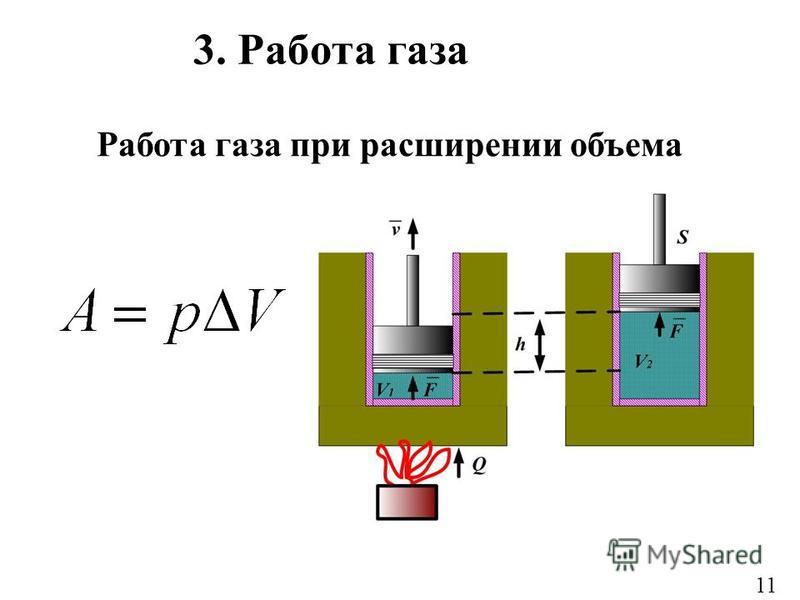 Работа, совершаемая газом, противоположна его начальному изменению внутренней энергии
Работа, совершаемая газом, противоположна его начальному изменению внутренней энергии Вт = -ΔU . Этот процесс описывает переходы, которые происходят быстро , и газ не успевает поглотить или отдать какое-либо тепло.
Расчетный пример
Предположим, что требуется найти изменение внутренней энергии, поглощенное тепло и работу, совершенную азотом, хранящимся внутри гибкого сосуда объемом 0,5 м³ при атмосферном давлении и температуре 250 К, нагретого до 300 К. В этом случае мы рассматриваем изобарический процесс.
Рассчитайте конечный объем:
V₂ = V₁ * T₂ / T₁ = 0,5 м³ * 300 K / 250 K = 0,6 м³,Рассчитать количество молекул:
n = p * V₁ / (R * T₁) = 101,325 кПа * 0,5 м³ / (8,314 Дж/(моль * K) * 250 K) = 24,375 моль,Найти теплоемкость
Cvазота, которая равна20,814 Дж/(моль*К)(для идеального двухатомного газа она должна быть равна20,786 Дж/(моль*К)),Оценка изменения внутренней энергии:
ΔU = 20,814 Дж/(моль * К) * 24,375 моль * 50 К = 25,367 кДж,Определить работу, совершаемую газом:
Вт = 101,325 кПа * 0,1 м³ = 10,133 кДж,А оцените теплоту, поглощенную азотом:
Q = 25,367 кДж + 10,133 кДж = 35,500 кДж
Вы всегда можете сэкономить свое время и воспользоваться нашим комбинированным газовым калькулятором!
Цикл Карно
Это один из циклов, который представляет модель идеального двигателя с максимально возможным КПД с точки зрения термодинамических законов.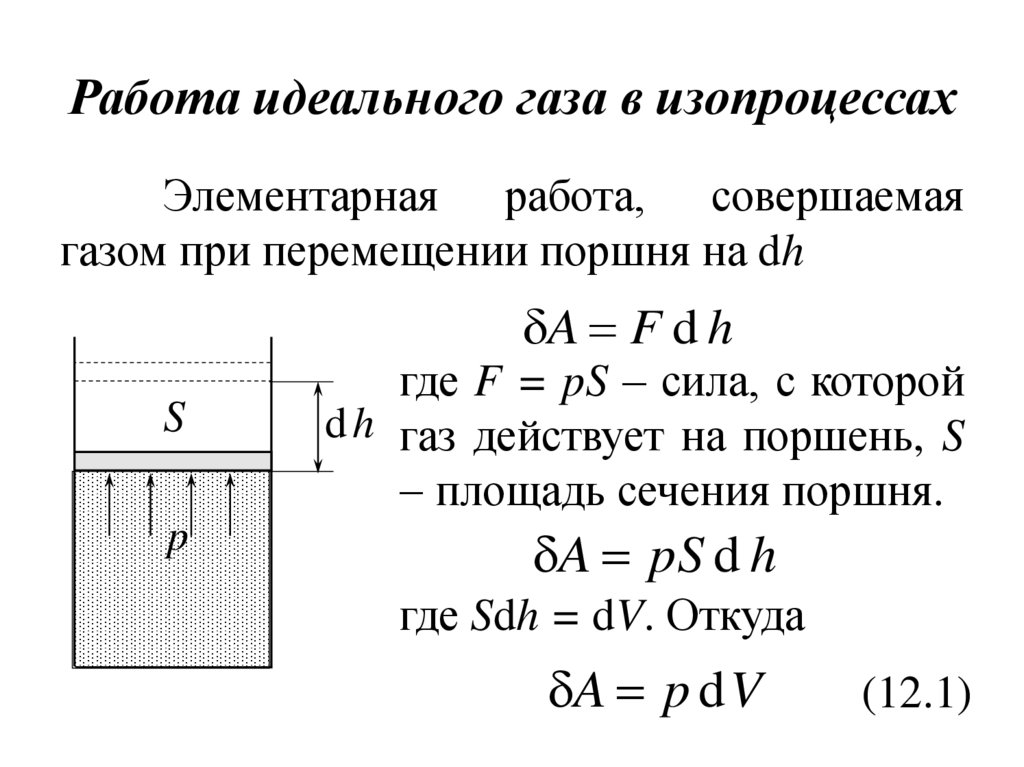 Он состоит из двух адиабатических и двух изотермических процессов. Этот двигатель поглощает тепло от горячего резервуара, преобразует его в работу и отдает оставшееся тепло холодному. С помощью этого калькулятора комбинированного газового закона вы можете спроектировать термодинамический цикл любого типа и узнать, как это изменение влияет на выходную эффективность!
Он состоит из двух адиабатических и двух изотермических процессов. Этот двигатель поглощает тепло от горячего резервуара, преобразует его в работу и отдает оставшееся тепло холодному. С помощью этого калькулятора комбинированного газового закона вы можете спроектировать термодинамический цикл любого типа и узнать, как это изменение влияет на выходную эффективность!
Войцех Сас, кандидат наук
Выберите тип процесса и газа
Процесс
Рабочий газ
Вставьте начальные параметры
Начальное давление (P₁)
Начальный объем (V₁)
Начальная температура (T₁)
)
Конечная температура (T₂)
Изменение внутренней энергии (ΔU)
Работа (Вт)
Теплота (Q)
Посмотреть 36 похожих термодинамических калькуляторов0003
Термодинамика — раздел физики
который имеет дело с энергией и работой системы.
Термодинамика занимается только
широкомасштабный ответ
системы, которую мы можем наблюдать
и измерить в опытах. Состояние газа определяется
значения некоторых измеряемых свойств
как давление,
температура,
а также
объем
которую занимает газ. Значения этих переменных и
состояние газа можно изменить. На этом рисунке мы показываем газ
в синей банке в двух разных состояниях. Слева, в штате
1 газ находится под более высоким давлением и занимает меньший объем, чем
в состоянии 2, справа. Мы можем изобразить состояние газа на графике
давления по отношению к объему, который
называется
диаграмма p-V
как показано справа.
Чтобы изменить состояние газа с состояния 1 на
Состояние 2, мы должны изменить условия в банке, либо нагревая
газ, или физически изменяющийся
объем, перемещая поршень, или изменяя давление, добавляя или удаляя
вес от поршня. В некоторых из этих изменений мы действительно работаем
на, или есть работа, выполненная газом, в других изменениях, которые мы добавляем, или
удалить тепло. Ученые определяют работу W как продукт силы F , действующей на расстоянии с : Вт = F * с Для газа работа есть произведение давление p и громкость V во время смены громкости. Вт = р * В Мы можем сделать быстрые единицы проверяют, чтобы увидеть, что давление сила / площадь умножить на объем площадь * длина дает единицы силы, умноженные на длину, которые являются единицами работы. W = (сила / площадь) * (площадь * длина) = сила * длина В метрической системе единицей работы является джоуль, в английской системе
единицей является фут-фунт. W = S [p] dV На графике зависимости давления от объема, работа – это площадь под кривой, описывает, как состояние изменяется с состояния 1 на состояние 2. Как упоминалось выше, существует несколько вариантов изменения состояния
газ из одного состояния в другое. Таким образом, мы можем ожидать, что количество
работа, совершаемая газом или газом, может быть разной в зависимости от того, как именно
изменен. В качестве примера на графике на рисунке изображена кривая
черная линия от состояния 1 до состояния 2 нашего ограниченного газа.
Эта линия представляет собой изменение, вызванное удалением весов
и уменьшая давление и позволяя объему регулироваться в соответствии с
по закону Бойля без подвода тепла. Обратите внимание, что не только работа, совершаемая газом, зависит от процесса, но и также тепло, переданное газу. В первом процессе кривая линия от из состояния 1 в состояние 2 теплота газу не передается; процесс был адиабатический . Но во втором процессе прямая линия из состояния 1 в состояние «а», а затем к Состояние 2, тепло передается газу в процессе постоянного давления. Теплота, передаваемая газу, зависит не только от начального и конечные состояния газа, но и процесс, используемый для изменения штат. Деятельность: Экскурсии с гидом
Навигация ..
|
12.2 Первый закон термодинамики: тепловая энергия и работа
Цели обученияДавление, объем, температура и закон идеального газаРабота давление–объемПервый закон термодинамикиРешение задач, связанных с первым законом термодинамикиПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать, как давление, объем и температура связаны друг с другом и работают на основе закона идеального газа
- Опишите работу давление-объем
- Опишите первый закон термодинамики словесно и математически
- Решить задачи, связанные с первым законом термодинамики
Давление, объем, температура и закон идеального газа
Перед рассмотрением первого закона термодинамики важно понять связь между давлением, объемом и температурой. Давление, P , определяется как
12.1P=FA,P=FA,
, где F — это сила, приложенная к площади A , которая перпендикулярна силе.
В зависимости от области, на которую она воздействует, данная сила может иметь существенно разный эффект, как показано на рис. 12.3.
Рис. 12.3 (а) Хотя человек, которого тыкают пальцем, может испытывать раздражение, сила не имеет длительного эффекта. (b) Напротив, та же самая сила, приложенная к участку размером с острый конец иглы, достаточно велика, чтобы повредить кожу.
(b) Напротив, та же самая сила, приложенная к участку размером с острый конец иглы, достаточно велика, чтобы повредить кожу.
Единицей измерения давления в системе СИ является паскалей , где 1 Па=1 Н/м2,1 Па=1 Н/м2.
Давление определяется для всех состояний вещества, но особенно важно при обсуждении жидкостей (например, воздуха). Вы, наверное, слышали, что слово давление используется по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления). Это только два из многих примеров давлений в жидкостях.
Связь между давлением, объемом и температурой идеального газа определяется законом идеального газа. Газ считается идеальным при низком давлении и достаточно высокой температуре, и силами между составляющими его частицами можно пренебречь. Закон идеального газа гласит, что
12.2PV=NkT.PV=NkT.
, где P — давление газа, V — занимаемый им объем, N — число частиц (атомов или молекул) в газе, а T — его абсолютная температура.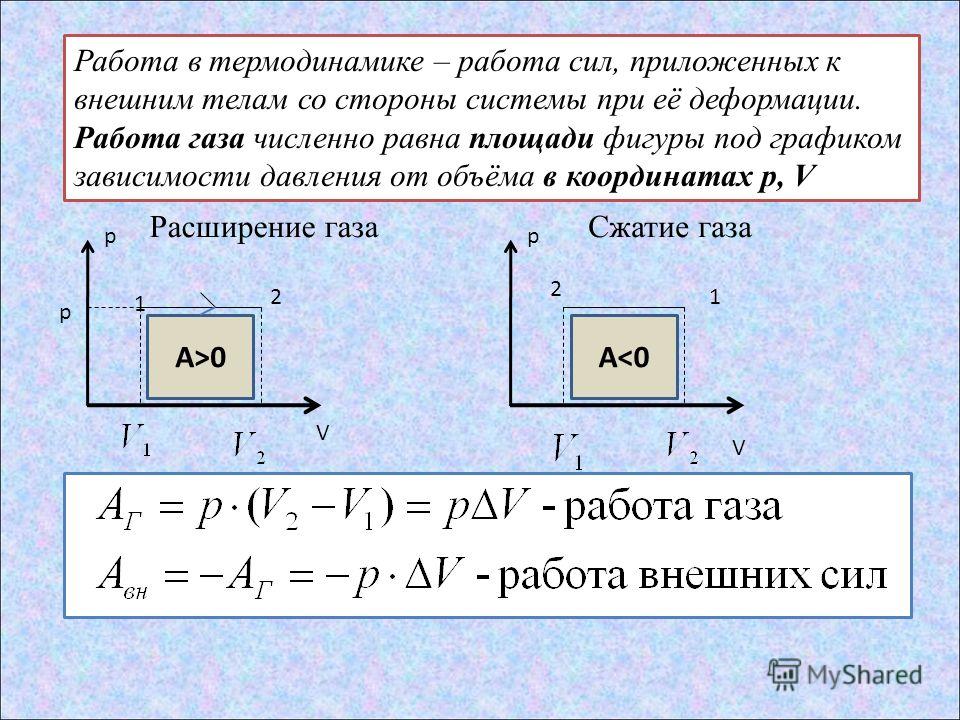 Константа k называется постоянной Больцмана и имеет значение k=1,38×10−23 Дж/К, k=1,38×10−23 Дж/К. газовый закон. Вместо этого нам важно заметить из уравнения, что для данной массы газа верно следующее:
Константа k называется постоянной Больцмана и имеет значение k=1,38×10−23 Дж/К, k=1,38×10−23 Дж/К. газовый закон. Вместо этого нам важно заметить из уравнения, что для данной массы газа верно следующее:
- Когда объем постоянный, давление прямо пропорционально температуре.
- Когда температура постоянна, давление обратно пропорционально объему.
- Когда давление постоянно, объем прямо пропорционален температуре.
Этот последний пункт описывает тепловое расширение — изменение размера или объема данной массы при изменении температуры. Что является основной причиной теплового расширения? Повышение температуры означает увеличение кинетической энергии отдельных атомов. Газы особенно подвержены тепловому расширению, хотя жидкости расширяются в меньшей степени при аналогичном повышении температуры, и даже твердые тела имеют незначительное расширение при более высоких температурах. Вот почему железнодорожные пути и мосты имеют компенсаторы, которые позволяют им свободно расширяться и сужаться при изменении температуры.
Чтобы получить некоторое представление о том, как связаны друг с другом давление, температура и объем газа, представьте, что происходит, когда вы накачиваете воздух в спущенную шину. Объем шины сначала увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине. Как только шина расширяется почти до своего полного размера, стенки ограничивают объемное расширение. Если вы продолжите накачивать воздух в шину (которая теперь имеет почти постоянный объем), давление будет увеличиваться с повышением температуры (см. рис. 12.4).
Рисунок 12.4 (а) Когда воздух нагнетается в спущенную шину, ее объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается по мере добавления воздуха. (c) Когда шина полностью накачана, давление в ней увеличивается с температурой.
Давление–Объем Работа
Работа давление-объем — это работа, совершаемая при сжатии или расширении жидкости.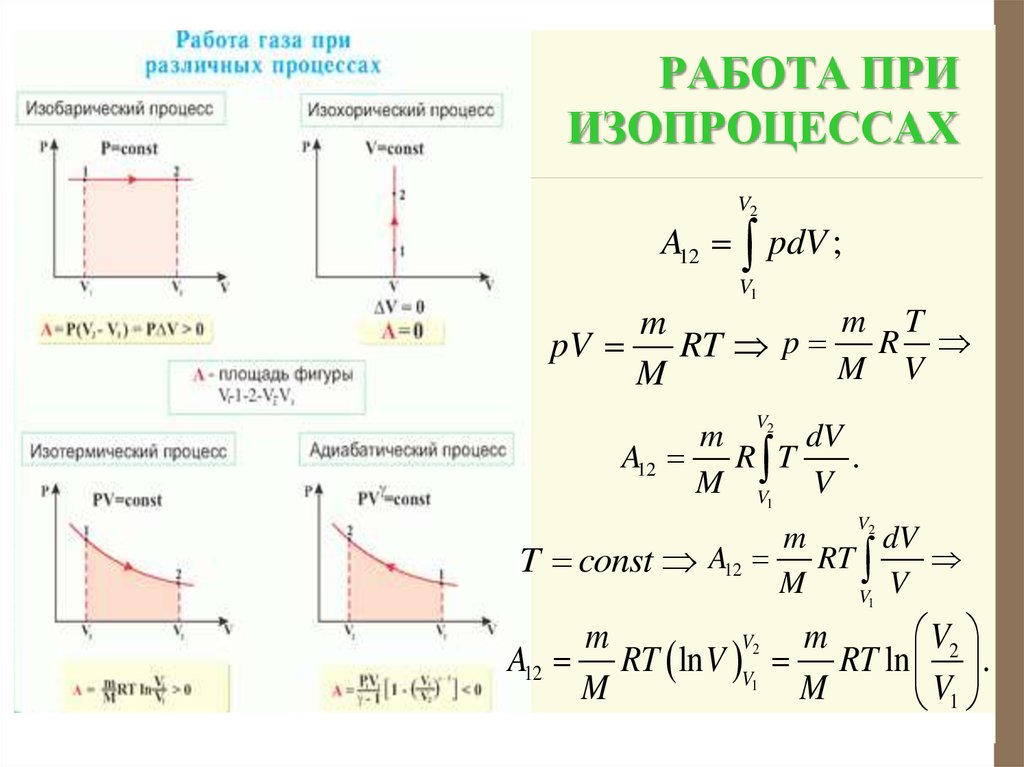 Всякий раз, когда происходит изменение объема, а внешнее давление остается постоянным, происходит работа давление-объем. При сжатии уменьшение объема увеличивает внутреннее давление в системе при совершении работы на систему. Во время расширения (рис. 12.5) увеличение объема снижает внутреннее давление в системе, поскольку система выполняет работу .
Всякий раз, когда происходит изменение объема, а внешнее давление остается постоянным, происходит работа давление-объем. При сжатии уменьшение объема увеличивает внутреннее давление в системе при совершении работы на систему. Во время расширения (рис. 12.5) увеличение объема снижает внутреннее давление в системе, поскольку система выполняет работу .
Рис. 12.5 Расширение газа требует передачи энергии для поддержания постоянного давления. Поскольку давление постоянно, совершаемая работа равна P∆VP∆V.
Напомним, что формула работы W=Fd.W=Fd. Мы можем изменить определение давления, P=FA,P=FA, чтобы получить выражение для силы через давление.
12.3F=ПАФ=ПА
Подставляя это выражение для силы в определение работы, получаем
12.4W=PAd.W=PAd.
Поскольку площадь, умноженная на смещение, представляет собой изменение объема, W=PΔVW=PΔV , математическое выражение для работы «давление-объем» равно
.
12,5W=PΔV.W=PΔV.
Точно так же, как мы говорим, что работа — это сила, действующая на расстоянии, для жидкостей мы можем сказать, что работа — это давление, действующее через изменение объема. Для работы давление-объем давление аналогично силе, а объем аналогичен расстоянию в традиционном определении работы.
Watch Physics
Работа с расширением
В этом видео описывается работа с расширением (или работа давление-объем). Сал комбинирует уравнения W=P∆VW=P∆V и ∆U=Q-W∆U=Q-W, чтобы получить ∆U=Q-P∆V∆U=Q-P∆V.
Воспроизвести видео «Работа из дополнения».
Проверка захвата
Если объем системы увеличивается, а давление остается постоянным, является ли значение работы, выполненной системой Вт , положительной или отрицательной? Приведет ли это к увеличению или уменьшению внутренней энергии системы?
- Положительный; внутренняя энергия уменьшится
- Положительный; внутренняя энергия увеличится
- Отрицательный; внутренняя энергия уменьшится
- Отрицательный; внутренняя энергия увеличится
Первый закон термодинамики
Теплота ( Q ) и работа ( W ) — два способа добавления или удаления энергии из системы. Процессы очень разные. Тепло вызывается разницей температур, а работа связана с силой, действующей на расстоянии. Тем не менее, теплота и работа могут давать одинаковые результаты. Например, оба могут вызвать повышение температуры. Тепло передает энергию в систему, например, когда солнце нагревает воздух в велосипедной шине и повышает температуру воздуха. Точно так же над системой может совершаться работа, например, когда велосипедист накачивает воздух в шину. После того, как произошло повышение температуры, невозможно сказать, было ли оно вызвано теплом или работой. И теплота, и работа представляют собой энергию в пути — ни одна из них не хранится как таковая в системе. Однако оба могут изменять внутреннюю энергию, U , системы.
Процессы очень разные. Тепло вызывается разницей температур, а работа связана с силой, действующей на расстоянии. Тем не менее, теплота и работа могут давать одинаковые результаты. Например, оба могут вызвать повышение температуры. Тепло передает энергию в систему, например, когда солнце нагревает воздух в велосипедной шине и повышает температуру воздуха. Точно так же над системой может совершаться работа, например, когда велосипедист накачивает воздух в шину. После того, как произошло повышение температуры, невозможно сказать, было ли оно вызвано теплом или работой. И теплота, и работа представляют собой энергию в пути — ни одна из них не хранится как таковая в системе. Однако оба могут изменять внутреннюю энергию, U , системы.
Внутренняя энергия представляет собой сумму кинетической и потенциальной энергий атомов и молекул системы. Ее можно разделить на множество подкатегорий, таких как тепловая и химическая энергия, и она зависит только от состояния системы (т.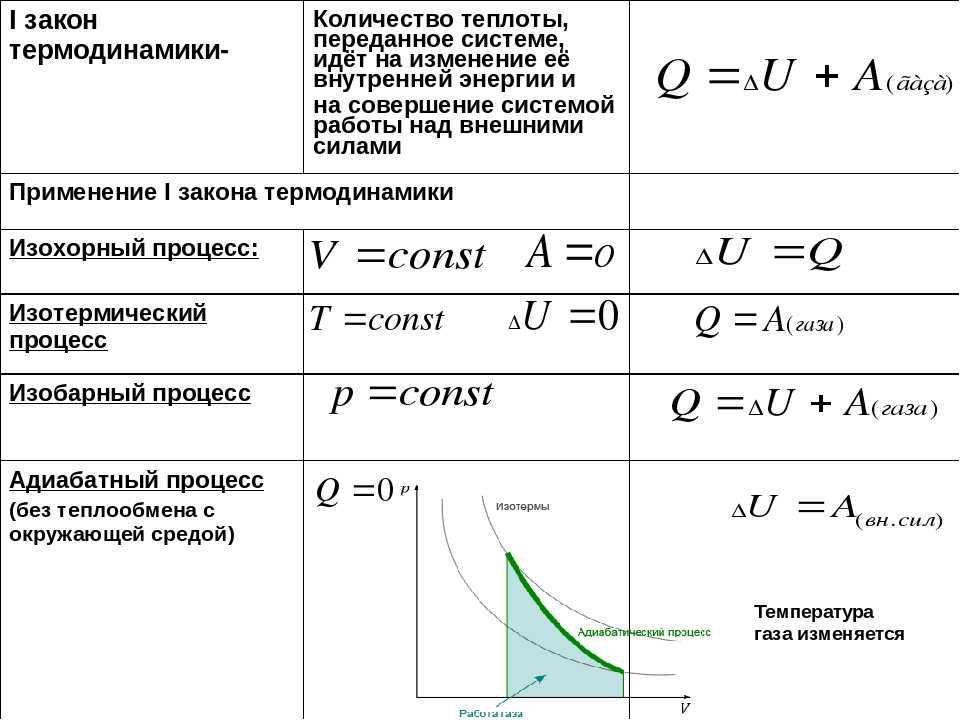 система.
система.
Чтобы понять взаимосвязь между теплом, работой и внутренней энергией, мы используем первый закон термодинамики. Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых теплота и работа являются методами передачи энергии в системы и из них. Его также можно использовать для описания того, как энергия, передаваемая теплом, преобразуется и снова передается за счет работы.
Советы для достижения успеха
Вспомним, что принцип сохранения энергии гласит, что энергия не может быть создана или уничтожена, но ее можно преобразовать из одной формы в другую.
Первый закон термодинамики гласит, что изменение внутренней энергии замкнутой системы равно чистой передаче тепла в систему минус сетевая работа, выполненная на систему. В форме уравнения первый закон термодинамики равен
.12,6ΔU=Q−W.ΔU=Q−W.
Здесь ΔUΔU — изменение внутренней энергии , U , системы. Как показано на рис. 12.6, Q представляет собой полезного тепла, переданного в систему , то есть Q представляет собой сумму всех теплопередач в систему и из нее. W — чистая работа, выполненная системой — то есть W — это сумма всей работы, проделанной системой или над ней. По соглашению, если Q положительное, то в систему имеет место чистый перенос тепла; если W положительно, то система выполняет чистую работу. Таким образом, положительный Q добавляет энергию в систему за счет тепла, а положительный W забирает энергию из системы за счет работы. Обратите внимание, что если тепло передает в систему больше энергии, чем та, которая совершается за счет работы, разница запасается в виде внутренней энергии.
Как показано на рис. 12.6, Q представляет собой полезного тепла, переданного в систему , то есть Q представляет собой сумму всех теплопередач в систему и из нее. W — чистая работа, выполненная системой — то есть W — это сумма всей работы, проделанной системой или над ней. По соглашению, если Q положительное, то в систему имеет место чистый перенос тепла; если W положительно, то система выполняет чистую работу. Таким образом, положительный Q добавляет энергию в систему за счет тепла, а положительный W забирает энергию из системы за счет работы. Обратите внимание, что если тепло передает в систему больше энергии, чем та, которая совершается за счет работы, разница запасается в виде внутренней энергии.
Рис. 12.6 Первый закон термодинамики — это принцип сохранения энергии, сформулированный для системы, где теплота и работа — это методы передачи энергии в систему и из нее. Q представляет чистую теплопередачу — это сумма всех передач энергии в виде тепла в систему и из нее. Q положителен для чистой теплопередачи в систему. WoutWout — это работа, проделанная системой, а WinWin — это проделанная работа на систему. W — это общая работа, выполненная в системе или на . W является положительным, когда на система выполняет больше работы, чем на на ней. Изменение внутренней энергии системы ΔUΔU связано с выделением тепла и работой согласно первому закону термодинамики: ΔU=Q−W. ΔU=Q−W.
ΔU=Q−W.
Из этого также следует, что отрицательный Q указывает на то, что энергия передается от из системы за счет тепла и, таким образом, уменьшает внутреннюю энергию системы, тогда как отрицательный W это работа над системой, которая увеличивает внутреннюю энергию.
Смотреть физику
Первый закон термодинамики/Внутренняя энергия
В этом видео объясняется первый закон термодинамики, сохранение энергии и внутренняя энергия. В нем рассматривается пример преобразования энергии между кинетической энергией, потенциальной энергией и теплопередачей из-за сопротивления воздуха.
Воспроизвести видео «Первый закон термодинамики».
Проверка захвата
Рассмотрим пример подбрасывания мяча при наличии сопротивления воздуха. Что, по вашему мнению, произойдет с конечной скоростью и конечной кинетической энергией мяча по мере увеличения сопротивления воздуха? Почему?
- Оба будут уменьшаться.
 Энергия передается воздуху за счет тепла из-за сопротивления воздуха.
Энергия передается воздуху за счет тепла из-за сопротивления воздуха. - Оба увеличатся. Энергия передается от воздуха к мячу за счет сопротивления воздуха.
- Конечная скорость увеличится, но конечная кинетическая энергия уменьшится. Энергия передается в виде тепла воздуху от мяча за счет сопротивления воздуха.
- Конечная скорость уменьшится, но конечная кинетическая энергия увеличится. Энергия передается теплом от воздуха к мячу за счет сопротивления воздуха.
Смотреть физику
Подробнее о внутренней энергии
В этом видео более подробно рассказывается о внутренней энергии и о том, как использовать уравнение ΔU=Q−W.ΔU=Q−W. Обратите внимание, что Сал использует уравнение ΔU=Q+WΔU=Q+W , где W — это работа, проделанная над системой, тогда как мы используем W для представления работы, выполненной системой .
Проиграть видео «Внутренняя энергия».
Проверка захвата
Если 5 Дж отводится теплом из системы, и система совершает 5 Дж работы, как изменится внутренняя энергия системы?
- −10 Дж
- 0Дж
- 10Дж
- 25Дж
Решение задач, связанных с первым законом термодинамики
Рабочий пример
Расчет изменения внутренней энергии
Предположим, что 40,00 Дж энергии передается системе в виде тепла, а система совершает 10,00 Дж работы. Далее из системы передается 25,00 Дж теплоты, а за счет работы над системой совершается 4,00 Дж. Каково чистое изменение внутренней энергии системы?
СТРАТЕГИЯ
Сначала необходимо рассчитать полезное тепло и чистую работу. Затем, используя первый закон термодинамики ΔU=Q−W, ΔU=Q−W, найдите изменение внутренней энергии.
Решение
Чистая теплота представляет собой передачу тепла в систему минус передачу тепла из системы, или
12,7Q=40,00 Дж-25,00 Дж=15,00 Дж. Q=40,00 Дж-25,00 Дж=15,00 Дж.
Q=40,00 Дж-25,00 Дж=15,00 Дж.
Полная работа – это работа, выполненная системой, за вычетом работы, выполненной над системой, или
12,8 Вт=10,00 Дж−4,00 Дж=6,00 Дж. Вт=10,00 Дж−4,00 Дж=6,00 Дж.
Изменение внутренней энергии определяется первым законом термодинамики.
12,9ΔU=Q−W=15,00 Дж−6,00 Дж=9,00 ДжΔU=Q−W=15,00 Дж−6,00 Дж=9.00 Дж
Обсуждение
Другой способ решения этой задачи состоит в том, чтобы найти изменение внутренней энергии для каждого из двух шагов в отдельности, а затем сложить два изменения, чтобы получить общее изменение внутренней энергии. Этот подход будет выглядеть следующим образом:
Для 40,00 Дж тепла и 10,00 Дж работы изменение внутренней энергии равно W1=40,00 Дж−10,00 Дж=30,00 Дж.
Для 25,00 Дж тепловыделения и 4,00 Дж работы изменения внутренней энергии равно
12,11ΔU2=Q2-W2=-25,00 Дж-(-4,00 Дж)=-21,00 Дж. ΔU2=Q2-W2=-25,00 Дж-(-4,00 Дж)=-21,00 Дж.
Общее изменение равно
12,12ΔU=ΔU1+ΔU2=30,00 Дж+(−21,00 Дж)=9,00 Дж. ΔU=ΔU1+ΔU2=30,00 Дж+(−21,00 Дж)=9,00 Дж. на ступени изменение внутренней энергии одинаково.
ΔU=ΔU1+ΔU2=30,00 Дж+(−21,00 Дж)=9,00 Дж. на ступени изменение внутренней энергии одинаково.
Рабочий пример
Расчет изменения внутренней энергии: одно и то же изменение в
U производится двумя разными процессамиКак изменится внутренняя энергия системы, если в общей сложности 150,00 Дж передано теплотой от системы и 159,00 Дж произведена работой над системой?
СТРАТЕГИЯ
Чистое тепло и работа уже даны, поэтому просто используйте эти значения в уравнении ΔU=Q−W.ΔU=Q−W.
Решение
Здесь чистая теплота и полная работа задаются непосредственно как Q=-150,00 Дж и W=-159,00 Дж, Q=-150,00 Дж и W=-159,00 Дж, так что
12,13ΔU=Q- Вт=-150,00 Дж-(-1590,00 Дж)=9,00 Дж.ΔU=Q-W=-150,00 Дж-(-159,00 Дж)=9,00 Дж.
Обсуждение
Рис. 12.8. Два разных процесса вызывают одно и то же изменение в системе. (а) Всего в систему поступает 15,00 Дж теплоты, а работа отнимает всего 6,00 Дж. Изменение внутренней энергии равно ΔU = Q – W = 9,00 Дж. (б) Теплопередачей отводится 150,00 Дж из система при работе вкладывает в нее 159,00 Дж, производя увеличение внутренней энергии на 9,00 Дж. Если система начинается в одном и том же состоянии в (а) и (б), она в конечном итоге окажется в одном и том же конечном состоянии в любом случае — ее конечное состояние связано с внутренней энергией, а не с тем, как эта энергия была приобретена.
Изменение внутренней энергии равно ΔU = Q – W = 9,00 Дж. (б) Теплопередачей отводится 150,00 Дж из система при работе вкладывает в нее 159,00 Дж, производя увеличение внутренней энергии на 9,00 Дж. Если система начинается в одном и том же состоянии в (а) и (б), она в конечном итоге окажется в одном и том же конечном состоянии в любом случае — ее конечное состояние связано с внутренней энергией, а не с тем, как эта энергия была приобретена.
Совершенно другой процесс во втором рабочем примере приводит к тому же изменению внутренней энергии на 9,00 Дж, что и в первом рабочем примере. Обратите внимание, что изменение в системе в обеих частях связано с ΔUΔU, а не с отдельными задействованными Q или W . Система оказывается в том же состоянии в обеих задачах. Обратите внимание, что, как обычно, на рис. 12.8 выше WoutWout — это работа, выполненная 90 439 на 90 440 системе, а WinWin — это работа, выполненная 90 439 на 90 440 системе.
Практические задачи
Какова работа давление-объем, совершаемая системой, если давление 20 Па вызывает изменение объема 3,0 м3?
- 0,15 Дж
- 6,7 Дж
- 23Дж
- 60Дж
Какова чистая теплота, выделяемая системой, если 25 Дж передается теплом в систему, а 45 Дж передается из нее?
- −70 Дж
- −20J
- 20Дж
- 70Дж
Проверьте свое понимание
Упражнение 3
Что такое давление?
- Давление равно силе, деленной на длину.
- Давление — это сила, деленная на площадь.
- Давление равно силе, деленной на объем.

- Давление — это сила, деленная на массу.
Упражнение 4
Что такое единица СИ для давления?
- паскалей или Н/м 3
- кулон
- ньютонов
- паскалей или Н/м 2
Упражнение 5
Что такое работа давление-объем?
- Работа, совершаемая при сжатии или расширении жидкости.
- Это работа, совершаемая силой над объектом для получения определенного перемещения.
- Это работа, которую совершают поверхностные молекулы жидкости.
- Это работа, которую совершают высокоэнергетические молекулы жидкости.
Упражнение 6
Когда считается, что работа давление-объем совершается В системе?
- При увеличении как объема, так и внутреннего давления.

- При снижении как объема, так и внутреннего давления.
- При снижении объема и повышении внутреннего давления.
- При увеличении объема и снижении внутреннего давления.
Упражнение 7
Какими способами можно добавить или убрать энергию из системы?
- Передача энергии с помощью тепла является единственным способом добавления энергии в систему или удаления энергии из нее.
- Выполнение работы сжатия — единственный способ добавить энергию в систему или убрать ее из системы.
- Выполнение работ по расширению — единственный способ добавить или убрать энергию из системы.
- Передача энергии с помощью тепла или выполнения работы — это способы добавления энергии в систему или удаления энергии из нее.
Упражнение 8
Что такое внутренняя энергия?
- Это сумма кинетических энергий атомов и молекул системы.

- Это сумма потенциальных энергий атомов и молекул системы.
- Это сумма кинетической и потенциальной энергий атомов и молекул системы.
- Это разница между величинами кинетической и потенциальной энергии атомов и молекул системы.
- Печать
- Поделиться
Работа
РаботаРабота
| Определение работы | Тепло и работа | Сохранение энергии | Внутренняя энергия |
| Взаимное превращение тепла и работы | Функции состояния | Калориметр | |
Определение работы
Работа может быть определена как произведение силы, используемой для перемещения
объект, умноженный на расстояние, на которое перемещается объект.
ш = F x г
Представьте себе систему, состоящую из образца аммиака, запертого в поршне и цилиндре, как показано на рисунке ниже. Предположим, что давление газа, давит на поршень просто уравновешивает вес поршня, так что объем газа остается постоянным. В настоящее время считать, что газ разлагается с образованием азота и водорода, увеличивая количество газа частицы в контейнере. Если температура и давление газа остаются постоянными, это означает, что объем газа должен увеличиться.
2 NH 3 ( г ) N 2 ( г ) + 3 Н 2 ( г )
Объем газа можно увеличить, частично вытолкнув поршень из цилиндра.
Совершаемая работа равна произведению силы, действующей на поршень, на
расстояние, на которое перемещается поршень.
ш = F x г
Давление ( P ), которое газ оказывает на поршень, равно силе (F) с которой он давит на поршень, деленную на площадь поверхности ( A ) поршень.
Таким образом, сила, действующая на газ, равна произведению его давления на площадь поверхности поршня.
F = P x A
Подстановка этого выражения в уравнение, определяющее работу, дает следующее результат.
w = ( P x A ) x d
Произведение площади поршня на расстояние, на которое перемещается поршень, равно изменение объема системы при расширении газа. Условно, изменение объема представлено символом В .
В = А х д
Таким образом, величина работы, совершаемой при расширении газа, равна произведению
давление газа, умноженное на изменение объема газа.
| с | = П В
Джоуль – измерение теплоты и работы
По определению, один джоуль — это работа, совершаемая, когда сила в один ньютон используется для перемещения объект один метр.
1 Дж = 1 Н·м
Поскольку работа может быть преобразована в теплоту и наоборот, система СИ использует джоуль для измерять энергию в виде теплоты и работы.
Первый закон термодинамики: сохранение Энергия
Первый закон термодинамики гласит, что энергия не может быть создана или
уничтожен. Система может получать или терять энергию. Но любое изменение энергии системы
должно сопровождаться эквивалентным изменением энергии его окружения, потому что
полная энергия Вселенной постоянна. Первый закон термодинамики можно описать
следующим уравнением.
E унив = E сис + E входящий = 0
(Индексы univ , sys и surr обозначают вселенную, системы и ее окружения.)
Внутренняя энергия
Энергию системы часто называют ее внутренней энергией , потому что она представляет собой сумму кинетической и потенциальной энергий частиц, образующих систему. Потому что отсутствие взаимодействия между частицами, единственный вклад во внутреннюю энергию идеального газа есть кинетическая энергия частиц. Внутренняя энергия идеального газа равна следовательно, прямо пропорциональна температуре газа.
(В этом уравнении R — постоянная идеального газа, а T — температура газа в единицах Кельвина.)
Хотя трудно, если вообще возможно, написать уравнение для более сложных
системы, внутренняя энергия системы по-прежнему прямо пропорциональна ее
температура. Поэтому мы можем использовать изменения температуры системы для мониторинга.
изменение его внутренней энергии.
Поэтому мы можем использовать изменения температуры системы для мониторинга.
изменение его внутренней энергии.
Величина изменения внутренней энергии системы определяется как разница между начальным и конечным значениями этой величины.
Е сис = E окончательная — E начальная
Поскольку внутренняя энергия системы пропорциональна ее температуре, E положительна при повышении температуры системы.
Первый закон термодинамики: взаимопревращение тепла и работы
Энергия может передаваться между системой и ее окружением до тех пор, пока энергия энергия, полученная одним из этих компонентов Вселенной, равна энергии, потерянной Другой.
Е сис = — E исп.
Энергия может передаваться между системой и ее окружением в виде либо
тепло ( q ) или рабочий ( w ).
Е сис = ч + ш
Когда тепло поступает в систему, это может привести к повышению температуры системы или Работа.
q = E сис — с
Правила знаков для связи между внутренней энергией системы и тепла , которое пересекает границу между системой и ее окружением, задано на рисунке ниже.
- Когда тепло, поступающее в систему, увеличивает температуру системы, внутренний энергия системы увеличивается, и E положительный.
- Когда температура системы снижается из-за выхода тепла из системы, E отрицательно.
Соглашение о знаках для отношения между работой и внутренней энергией система показана в левой части рисунка ниже.
- Когда система воздействует на окружающую среду, энергия теряется, и E отрицательно.

- Когда окружающая среда воздействует на систему, внутренняя энергия системы становится больше, поэтому E положительный.
Соотношение между величиной работы, совершаемой системой при ее расширении, и изменение объема системы ранее описывалось следующим уравнением.
| с | = П В
На приведенном выше рисунке показано, что можно включить соглашение о знаках для работы расширения. записав это уравнение следующим образом.
w = — P В
Функции состояния
Когда уравнения связывают два или более свойств, описывающих гос. системы, они называются уравнениями состояния . Например, закон идеального газа уравнение состояния.
PV = нРТ
Функция состояния s зависит только от состояния системы, а не от
путь, используемый для достижения этого состояния.
Температура является функцией состояния. Сколько бы раз мы ни нагревали, ни охлаждали, ни расширяли, сжать или иным образом изменить систему, чистое изменение температуры зависит только от на начальное и конечное состояния системы.
Т = T окончательный — T начальный
То же самое можно сказать об объеме, давлении и числе молей газа в образец. Все эти величины являются функциями состояния.
Теплота и работа являются , а не функциями состояния. Работа не может быть функцией государства, потому что она
пропорциональна расстоянию, на которое перемещается объект, которое зависит от пути, по которому он двигался
от начального до конечного состояния. Если работа не является функцией состояния, то теплота не может быть
государственная функция либо. Согласно первому закону термодинамики изменение
внутренняя энергия системы равна сумме переданной теплоты и работы
между системой и ее окружением.
Е сис = ч + ш
Если E зависит не от пути перехода от начального состояния к конечному, а от количества работы зависит от используемого пути, количество отдаваемой или поглощаемой теплоты должно зависеть на пути.
Термодинамические свойства системы, являющиеся функциями состояния обычно обозначаются заглавными буквами ( T , V , P , E и так далее на). Термодинамические свойства, не являющиеся функциями состояния, часто описываются формулой строчные буквы ( q и w ).
| Практическая задача 3: Что из следующего свойства газа являются функциями состояния? (а) Температура, T (б) Объем, В (с) Давление, P (d) Количество молей газа, n (e) Внутренняя энергия, E Нажмите здесь, чтобы проверить свой ответ на практическое задание 3 |
Измерение тепла с помощью калориметра
Количество теплоты, выделяемой или поглощаемой в ходе химической реакции, можно измерить с помощью
калориметр, как показано на рисунке ниже.
Поскольку реакция происходит в закрытом сосуде при постоянном объеме, никакая работа расширение происходит во время реакции. Теплота, выделяемая или поглощаемая в результате реакции, равна равно изменению внутренней энергии системы за время реакция:
Е сис = q В .
Количество теплоты, отдаваемое или поглощаемое водой в калориметре, может быть рассчитывается исходя из теплоемкости воды.
| Практическая задача 4: Природный газ в метан реагирует с кислородом с образованием углекислого газа и воды. CH 4 ( г ) + 2 O 2 ( г ) CO 2 ( г ) + 2 H 2 O(4) Рассчитайте теплоту, выделяющуюся при взаимодействии 0,160 г метана с избытком кислорода в
бомбовый калориметр, если температура 1000 кг воды в ванне, окружающей
бомба увеличивается на 1,918 или С. Нажмите здесь, чтобы проверить свой ответ на практическое задание 4 Нажмите здесь, чтобы увидеть решение практической задачи 4 |
Тепло — это экстенсивное количество . Наиболее распространенный способ преобразования Измерение теплоты в интенсивную величину заключается в вычислении теплоты реакции в единиц килоджоулей на моль. Результатом этого расчета является величина, известная как молярный теплота реакции . По определению, молярная теплота реакции – это теплота, выделяемая или поглощается реакцией, выраженной в килоджоулях на моль одного из реагентов в реакции.
Закон идеального газа | безграничная физика |
Уравнения состояния
Закон идеального газа — это уравнение состояния гипотетического идеального газа (в котором нет взаимодействия между молекулами).
Цели обучения
Расскажите, как был выведен закон идеального газа.
Основные выводы
Ключевые моменты
Ключевые термины
- моль : В Международной системе единиц — основная единица количества вещества; количество вещества системы, которая содержит столько элементарных частиц, сколько атомов содержится в 12 г углерода-12. Символ: мол.
- идеальный газ : Гипотетический газ, молекулы которого не взаимодействуют друг с другом и испытывают упругие столкновения друг с другом и со стенками сосуда.
- Число Авогадро : количество составляющих частиц (обычно атомов или молекул) в одном моле данного вещества. Он имеет размерность, обратную молям, и его значение равно 6,02214129·1023 моль-1
Закон идеального газа – это уравнение состояния гипотетического идеального газа (иллюстрация приведена в ). В идеальном газе межмолекулярное взаимодействие отсутствует, и допускаются только упругие столкновения. Это хорошее приближение к поведению многих газов во многих условиях, хотя оно имеет несколько ограничений. Впервые он был сформулирован Эмилем Клапейроном в 1834 году как комбинация закона Бойля и закона Шарля.
В идеальном газе межмолекулярное взаимодействие отсутствует, и допускаются только упругие столкновения. Это хорошее приближение к поведению многих газов во многих условиях, хотя оно имеет несколько ограничений. Впервые он был сформулирован Эмилем Клапейроном в 1834 году как комбинация закона Бойля и закона Шарля.
Атомы и модули в газе : Атомы и молекулы в газе обычно сильно разделены, как показано. Поскольку на этих расстояниях силы между ними довольно слабы, их часто описывают законом идеального газа.
Эмпирический вывод
Закон Бойля утверждает, что давление P и объем V данной массы замкнутого газа обратно пропорциональны:
P∝1V\text{P} \propto \frac{1}{\text{V}}P∝V1
,
, а закон Шарля гласит, что объем газа пропорционален абсолютной температуре T газа при постоянном давлении
V∝T\text{V} \propto \text{T}V∝T
.
Комбинируя два закона, мы получаем
PVT=C\frac{\text{PV}}{\text{T}} = \text{C}TPV=C
,
где C константа, которая прямо пропорциональна количеству газа n (представляющему количество молей).
Коэффициент пропорциональности представляет собой универсальную газовую постоянную R, т. е. C = nR.
Следовательно, закон идеального газа
PV=nRT\text{PV} = \text{nRT}PV=nRT
.
Эквивалентно это может быть записано как
PV=NkT\text{PV} = \text{NkT}PV=NkT
,
, где k — постоянная Больцмана, а N — число молекул.
(Поскольку N = nN A , вы можете видеть, что
R=NAk\text{R} = \text{N}_\text{Ak}R=NAk
, где N A равно Число Авогадро. )
Обратите внимание, что эмпирический вывод не учитывает микроскопические детали. Однако уравнение можно вывести из первых принципов классической термодинамики (что выходит за рамки этого атома). 92}PV=31Nmv2
92}PV=31Nmv2
.
Изотермы
Изотермический процесс – это изменение системы, при котором температура остается постоянной: ΔT = 0.
Цели обучения
Укажите условия, при которых могут протекать изотермические процессы.
Ключевые выводы
Ключевые моменты
- Изотермические процессы обычно происходят, когда система находится в контакте с внешним тепловым резервуаром (тепловой баней), и изменение происходит достаточно медленно, чтобы позволить системе постоянно приспосабливаться к температуре резервуара за счет теплообмена.
- Для идеального газа, согласно закону идеального газа PV = NkT, PV остается постоянным в изотермическом процессе. Кривая на диаграмме PV, порожденная уравнением PV = const, называется изотермой.
- Для изотермического обратимого процесса работа, совершаемая газом, равна площади под соответствующей изотермой давление-объем.
 Он задается как
Он задается какWA→B=NkTlnVBVA\text{W}_{\text{A}\to \text{B}} = \text{NkT}\ln{\frac{\text{V}_ \text{B}}{\text{V}_\text{A}}}WA→B=NkTlnVAVB
.
Ключевые термины
- адиабатический : Возникающий без поступления или потери тепла.
- внутренняя энергия : Сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно энергии, необходимой для создания системы, за исключением энергии, необходимой для смещения ее окружения.
- идеальный газ : Гипотетический газ, молекулы которого не взаимодействуют друг с другом и испытывают упругие столкновения друг с другом и со стенками сосуда.
Изотермический процесс — это изменение системы, при котором температура остается постоянной: ΔT = 0. Обычно это происходит, когда система находится в контакте с внешним тепловым резервуаром (тепловой баней), и изменение происходит достаточно медленно, чтобы позволить системе постоянно подстраиваться под температуру резервуара посредством теплообмена. Напротив, адиабатический процесс происходит, когда система не обменивается теплом с окружающей средой (Q = 0). Другими словами, в изотермическом процессе значение ΔT = 0, но Q ≠ 0, а в адиабатическом процессе ΔT ≠ 0, но Q = 0,9.0003
Напротив, адиабатический процесс происходит, когда система не обменивается теплом с окружающей средой (Q = 0). Другими словами, в изотермическом процессе значение ΔT = 0, но Q ≠ 0, а в адиабатическом процессе ΔT ≠ 0, но Q = 0,9.0003
Для идеального газа произведение PV (P: давление, V: объем) является константой, если газ поддерживается в изотермических условиях (закон Бойля). Согласно закону идеального газа значение константы равно NkT, где N — число молекул газа, а k — постоянная Больцмана.
Это означает, что
p=NkTV=ConstantV\text{p} = {\text{N} \text{k} \text{T} \over \text{V}} = {\text{Constant} \ over \text{V}}p=VNkT=VConstant
.
Семейство кривых, генерируемых этим уравнением, показано на графике, представленном в . Каждая кривая называется изотермой. Такие графики называются индикаторными диаграммами — они впервые использовались Джеймсом Уаттом и другими для контроля эффективности двигателей. Температура, соответствующая каждой кривой на рисунке, увеличивается от левого нижнего угла к правому верхнему. 9{\text{V}_\text{B}}\text{P}\,\text{dV}WA→B=∫VAVBPdV
9{\text{V}_\text{B}}\text{P}\,\text{dV}WA→B=∫VAVBPdV
.
(Это уравнение получено в нашем атоме для «постоянного давления» в соответствии с кинетической теорией. Обратите внимание, что P = F/A. Это определение согласуется с нашим определением работы как силы, умноженной на расстояние.)
Для изотермического обратимого процесса , этот интеграл равен площади под соответствующей изотермой давление-объем и показан синим цветом для идеального газа. Опять же, применяется P = nRT / V, и при постоянной T (поскольку это изотермический процесс) мы имеем: 9{\ text {V} \ text {\ textunderscore} \ text {B}} \ frac {\ text {NkT}} {\ text {V}} \ text {dV} \\ &= \ text {NkT} \ ln {\ frac {\ text {V} \ text {\ textunderscore} \ text {B}} {\ text {V} \ text {\ textunderscore} \ text {A}}} \ end {align} W_A → B= ∫_V_AV_BpdV=∫_V_AV_BVNkTdV=NkTlnV_AV_B
.
По соглашению работа определяется как работа, которую система выполняет в своей среде. Если, например, система расширяется поршнем, движущимся в направлении силы, приложенной внутренним давлением газа, то работа считается положительной. Поскольку эта работа выполняется с использованием внутренней энергии системы, в результате внутренняя энергия уменьшается. И наоборот, если среда воздействует на систему так, что ее внутренняя энергия увеличивается, эта работа считается отрицательной (подробности о внутренней энергии см. в нашем атоме «Внутренняя энергия идеального газа»).
Если, например, система расширяется поршнем, движущимся в направлении силы, приложенной внутренним давлением газа, то работа считается положительной. Поскольку эта работа выполняется с использованием внутренней энергии системы, в результате внутренняя энергия уменьшается. И наоборот, если среда воздействует на систему так, что ее внутренняя энергия увеличивается, эта работа считается отрицательной (подробности о внутренней энергии см. в нашем атоме «Внутренняя энергия идеального газа»).
Постоянное давление
Изобарический процесс — это термодинамический процесс, при котором давление остается постоянным (при постоянном давлении работа, совершаемая газом, равна
PΔV\text{P} \Delta \text{V}PΔV
).
Цели обучения
Описать поведение одноатомного газа при изобарических процессах.
Ключевые выводы
Ключевые моменты
- Газы могут расширяться или сжиматься при определенных ограничениях.
 В зависимости от ограничения конечное состояние газа может измениться.
В зависимости от ограничения конечное состояние газа может измениться. - Тепло, переданное системе, совершает работу, но также изменяет внутреннюю энергию системы. В изобарическом процессе для одноатомного газа теплота и изменение температуры удовлетворяют следующему уравнению:
Q=52NkΔT\text{Q} = \frac{5}{2} \text{N} \text{k} \Delta \ текст{T}Q=25NkΔT
. - Для одноатомного идеального газа удельная теплоемкость при постоянном давлении равна
52R\frac{5}{2} \text{R}25R
.
Ключевые термины
- первый закон термодинамики : Вариант закона сохранения энергии: изменение внутренней энергии замкнутой системы равно количеству тепла, подведенного к системе, за вычетом количества работы, совершаемой системой над окружающей средой.
- удельная теплоемкость : Отношение количества теплоты, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству теплоты, необходимому для повышения температуры той же массы воды на ту же величину.

При определенном ограничении (например, давлении) газы могут расширяться или сжиматься; в зависимости от типа ограничения конечное состояние газа может измениться. Например, идеальный газ, расширяющийся при неизменной температуре (так называемый изотермический процесс), будет существовать в другом состоянии, чем газ, который расширяется при постоянном давлении (так называемый изобарический процесс). Этот атом посвящен изобарическому процессу и связанным с ним терминам. Мы обсудим изотермический процесс в следующем атоме.
Изобарический процесс
Изобарический процесс — это термодинамический процесс, при котором давление остается постоянным: ΔP = 0. Для идеального газа это означает, что объем газа пропорционален его температуре (исторически это называется законом Шарля). Давайте рассмотрим случай, когда газ действует на поршень при постоянном давлении P, ссылаясь на рис. 1 в качестве иллюстрации. Поскольку давление постоянно, прилагаемая сила постоянна, а выполненная работа определяется как W = Fd, где F (= PA) — сила, действующая на поршень под действием давления, а d — смещение поршня. Следовательно, работа, совершаемая газом (W), равна:
Поскольку давление постоянно, прилагаемая сила постоянна, а выполненная работа определяется как W = Fd, где F (= PA) — сила, действующая на поршень под действием давления, а d — смещение поршня. Следовательно, работа, совершаемая газом (W), равна:
W=PAd\text{W} = \text{PAd}W=PAd
.
Поскольку изменение объема цилиндра равно площади его поперечного сечения A, умноженной на смещение d, мы видим, что Ad=ΔV, изменение объема. Таким образом,
W=PΔV\text{W}= \text{P} \Delta \text{V}W=PΔV
(как видно на рис. 2 — изобарический процесс). Примечание: если ΔV положительно, то и W положительно, а это означает, что работа совершается газом во внешнем мире. Используя закон идеального газа PV=NkT (P=const),
Рис. 2 : График зависимости давления от объема для процесса с постоянным давлением или изобарического процесса. Площадь под кривой равна работе, совершаемой газом, поскольку W=PΔV.
W=NkΔT\text{W} = \text{Nk}\Delta \text{T}W=NkΔT
(уравнение 1) для идеального газа, подвергающегося изобарическому процессу.
Одноатомный газ
Согласно первому закону термодинамики,
Q=ΔU+W \text{Q} = \Delta \text{U} + \text{W}\,Q=ΔU+W
(уравнение 2), где W — работа, совершаемая системой, U — внутренняя энергия, Q — теплота. Закон гласит, что тепло, переданное системе, совершает работу, но также изменяет внутреннюю энергию системы. С
U=32NkT\text{U} = \frac{3}{2}\text{NkT}U=23NkT
для одноатомного газа получаем
ΔU=32NkΔT\Delta \text{U} = \frac{3}{2} \text{Nk} \Delta \text{T}ΔU=23NkΔT
(уравнение 3; подробности о внутренней энергии см. в нашем атоме в статье «Внутренняя энергия идеального Газ»). Используя уравнения 1 и 3, уравнение. 2 можно записать как:
Q=52NkΔT\text{Q} = \frac{5}{2} \text{N} \text{k} \Delta \text{T}Q=25NkΔT
для одноатомный газ в изобарическом процессе.
Удельная теплоемкость
Удельная теплоемкость при постоянном давлении определяется следующим уравнением:
Q=ncPΔT\text{Q} = \text{n} \text{c}_\text{P} \Delta \text{T}Q=ncP ΔТ
.
Здесь n — количество частиц в газе, выраженное в молях. Отметив, что N=N A n и R = kN A (N A : число Авогадро, R: универсальная газовая постоянная), получаем:
cP=52kNA=52R\text{c}_\ text{P} = \frac{5}{2} \text{kN}_\text{A} = \frac{5}{2} \text{R}cP=25kNA=25R
для одноатомного газа.
Решение проблем
С помощью закона идеального газа мы можем рассчитать давление, объем или температуру, а также количество молей газа в идеальных термодинамических условиях.
Цели обучения
Назовите шаги, используемые для решения уравнения идеального газа.
Ключевые выводы
Ключевые моменты
- Запишите всю известную вам информацию о газе и при необходимости переведите известные значения в единицы СИ.
- Выберите соответствующее уравнение газового закона, которое позволит вам рассчитать неизвестную переменную, и подставьте известные значения в уравнение.
 Затем вычислите неизвестную переменную.
Затем вычислите неизвестную переменную. - Общее газовое уравнение применяется только в том случае, если молярное количество газа фиксировано.
Ключевые термины
- идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и испытывают упругие столкновения друг с другом и со стенками сосуда.
- Единицы СИ : Международная система единиц (сокращенно СИ от французского: Le Système international d’unités). Это современная форма метрической системы.
Закон идеального газа — это уравнение состояния гипотетического идеального газа. Это хорошее приближение к поведению многих газов во многих условиях, хотя оно имеет несколько ограничений. Он наиболее точен для одноатомных газов при высоких температурах и низких давлениях.
Закон идеального газа имеет вид:
PV=nRT\text{PV}= \text{nRT}PV=nRT
,
где R — универсальная газовая постоянная, по ней можно найти значения давления P, объема V, температуры T, или количество молей n при определенных идеальных термодинамических условиях . Как правило, вам дается достаточно параметров для вычисления неизвестного. Вариации уравнения идеального газа могут помочь легко решить проблему. Вот несколько общих советов.
Как правило, вам дается достаточно параметров для вычисления неизвестного. Вариации уравнения идеального газа могут помочь легко решить проблему. Вот несколько общих советов.
Закон идеального газа также может быть представлен в виде:
PV=NkT\text{PV}= \text{NkT}PV=NkT
,
где N — число частиц в газе, k — постоянная Больцмана.
Чтобы решить уравнение идеального газа:
- Запишите всю информацию, которую вы знаете о газе.
- При необходимости переведите известные значения в единицы СИ.
- Выберите соответствующее уравнение газового закона, которое позволит вам рассчитать неизвестную переменную.
- Подставьте известные значения в уравнение. Вычислите неизвестную переменную.
Помните, что общее газовое уравнение применимо только в том случае, если молярное количество газа фиксировано. Например, если газ смешивается с другим газом, вам, возможно, придется применить уравнение отдельно для отдельных газов.
Пример
Представим, что в начале пути шина грузового автомобиля имеет объем 30 000 см 3 и внутреннее давление 170 кПа. Температура шины 16 ∘ С. К концу поездки объем шины увеличился до 32 000 см 3 и температура воздуха внутри шины 40 ∘ С. Какое давление в шинах в конце пути?
Давление в шинах : Давление в шинах может значительно меняться во время эксплуатации автомобиля. В основном это связано с изменением температуры воздуха в шинах.
Решение:
Шаг 1. Запишите всю известную вам информацию о газе: P 1 = 170 кПа и P 2 неизвестно. V 1 = 30 000 см 3 и V 2 = 32 000 см 3 . T 1 = 16 ∘ C и T 2 = 40 ∘ C.
Шаг 2. При необходимости преобразуйте известные значения в единицы СИ: Здесь температура должна быть преобразована в кельвины. Следовательно, T 1 = 16 + 273 = 289 K, T 2 = 40 + 273 = 313 K
Следовательно, T 1 = 16 + 273 = 289 K, T 2 = 40 + 273 = 313 K
Шаг 3. Выберите соответствующее уравнение газового закона, которое позволит вам вычислить неизвестную переменную: Мы можем использовать общее уравнение газа для решения этой задачи:
P1V1T1=P2V2T2\frac{\text{P}_1 \text{V}_1}{\text{T}_1} = \frac{\text{P}_2 \text{V}_2}{\text{ T}_2}T1P1V1=T2P2V2
.
Следовательно,
P2=P1×V1×T2T1×V2\text{P}_2 = \frac{\text{P}_1 \times \text{V}_1 \times \text{T}_2}{\ text{T}_1 \times \text{V}_2}P2=T1×V2P1×V1×T2
.
Шаг 4. Подставьте известные значения в уравнение. Вычислите неизвестную переменную:
P2 = 170 × 30 000 × 313 289 × 32 000 = 173 кПа\text{P}_2 = \frac{170\times 30 000 \times 313}{289\times 32 000} = 173~\text{кПа}P2=289×32 000170×30 000×313=173 кПа
.
Давление в шине в конце пути 173 кПа.
Обратите внимание, что на шаге 2 мы не удосужились преобразовать значения объема в m 3 . На шаге 4 давление появляется как в числителе, так и в знаменателе. В этом случае преобразование не требовалось.
Номер Авогадора
Число молекул в моле называется числом Авогадро (N A ) и определяется как 6,02 x 10 9 .0198 23 моль -1 .
Цели обучения
Объясните связь между числом Авогадро и родинкой.
Ключевые выводы
Ключевые моменты
- Авогадро выдвинул гипотезу о том, что равные объемы газа при одинаковых давлении и температуре содержат одинаковое количество молекул независимо от типа газа.
- Постоянная Авогадро является масштабным коэффициентом между макроскопическими и микроскопическими (в атомном масштабе) наблюдениями за природой. Он обеспечивает связь между другими физическими константами и свойствами.

- Альберт Эйнштейн предположил, что число Авогадро можно определить на основе величин, наблюдаемых в броуновском движении. Числовая апертура впервые была измерена Жаном Батистом Перреном в 1908 году.
Ключевые термины
- газовая постоянная : Универсальная постоянная R, фигурирующая в законе идеального газа (PV = nRT), полученная из двух фундаментальных констант, постоянной Больцмана и числа Авогадро (R = NAk). .
- Постоянная Фарадея : Величина электрического заряда на моль электронов.
- Броуновское движение : Беспорядочное движение взвешенных в жидкости частиц, возникающее в результате столкновения этих частиц с отдельными молекулами жидкости.
При измерении количества вещества иногда проще работать с единицей, отличной от количества молекул. Моль (сокращенно моль) — основная единица Международной системы единиц (СИ). Он определяется как любое вещество, содержащее столько атомов или молекул, сколько содержится ровно в 12 граммах (0,012 кг) углерода-12. Фактическое число атомов или молекул в одном моле называется 9.0932 Постоянная Авогадро (N A ) , по признанию итальянского ученого Амедео Авогадро.
Фактическое число атомов или молекул в одном моле называется 9.0932 Постоянная Авогадро (N A ) , по признанию итальянского ученого Амедео Авогадро.
Амадео Авогадро : Амедео Авогадро (1776–1856). Он установил, что соотношение между массами одного и того же объема различных газов (при одинаковых температуре и давлении) соответствует соотношению между их соответствующими молекулярными массами.
Число Авогадро (N) относится к числу молекул в одной грамм-молекуле кислорода. Это указывает на количество вещества, а не на независимое измерение измерения. В 1811 г. Амедео Авогадро впервые предположил, что объем газа (при данном давлении и температуре) пропорционален числу атомов или молекул независимо от природы газа (т. е. это число универсально и не зависит от типа газа). газ). В 1926 января Жан Перрен получил Нобелевскую премию по физике в основном за свою работу по определению постоянной Авогадро (несколько различных методов). Значение постоянной Авогадро N A равно 6,02×10 23 моль -1 .
Значение постоянной Авогадро N A равно 6,02×10 23 моль -1 .
Роль в науке
Постоянная Авогадро — это масштабный коэффициент между макроскопическими и микроскопическими (в атомном масштабе) наблюдениями за природой. Таким образом, он обеспечивает связь между другими физическими константами и свойствами. Например, он устанавливает связь между газовой постоянной R и постоянной Больцмана k, 9{-1}}F=NAe=96485,3383(83) смоль−1
.
Измерительный N
A Определение N A имеет решающее значение для расчета массы атома, поскольку последняя получается путем деления массы моля газа на постоянную Авогадро. В своем исследовании броуновского движения в 1905 году Альберт Эйнштейн предположил, что эту константу можно определить на основе величин, наблюдаемых в броуновском движении. Впоследствии идея Эйнштейна была проверена, что привело к первому определению N A в 1908 году благодаря экспериментальной работе Жана Батиста Перрена.
Абсолютная температура
Абсолютная температура является наиболее часто используемой термодинамической единицей температуры и является стандартной единицей температуры.
Цели обучения
Опишите зависимость между абсолютной температурой и кинетической энергией.
Ключевые выводы
Ключевые моменты
- Температура возникает из-за кинетической энергии случайных движений составляющих частиц материи, таких как молекулы или атомы. Поэтому разумно выбрать в качестве точки отсчета абсолютный нуль, где все классическое движение прекращается.
- По международному соглашению единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой стандартной воды.
- При абсолютном нуле частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее. Они сохраняют минимальное квантово-механическое движение.
Ключевые термины
- абсолютный ноль : Самая низкая возможная температура: ноль по шкале Кельвина и приблизительно -273,15°C и -4590,67°F.
 Полное отсутствие тепла; температура, при которой движение всех молекул прекратится.
Полное отсутствие тепла; температура, при которой движение всех молекул прекратится. - Международная система единиц : (SI): Стандартный набор основных единиц измерения, используемый в научной литературе по всему миру.
- Венский стандарт среднего значения морской воды : Стандарт, определяющий стандартизованный изотопный состав воды.
Термодинамическая температура является абсолютной мерой температуры. Это один из основных параметров термодинамики и кинетической теории газов. Термодинамическая температура является «абсолютной» шкалой, потому что она является мерой фундаментального свойства, лежащего в основе температуры: ее нулевая или нулевая точка («абсолютный ноль») — это температура, при которой частицы, составляющие материю, имеют минимальное движение и не могут стать еще холоднее. То есть они имеют минимальное движение, сохраняя только квантово-механическое движение, как показано на схеме 9. 0003
0003
График зависимости давления от температуры : График зависимости давления от температуры для различных газов при постоянном объеме. Обратите внимание, что все графики экстраполированы на нулевое давление при той же температуре
В простейшем случае «температура» возникает из-за кинетической энергии случайных движений составляющих частиц материи, таких как молекулы или атомы, как показано на рис. (T=0) нашей температурной системы. Используя абсолютную шкалу температур (система Кельвина), которая является наиболее часто используемой термодинамической температурой, мы показали, что средняя поступательная кинетическая энергия (КЭ) частицы в газе имеет простую связь с температурой:
Поступательное движение гелия : Реальные газы не всегда ведут себя в соответствии с идеальной моделью при определенных условиях, таких как высокое давление. Здесь показано, что размер атомов гелия относительно расстояния между ними увеличивается при давлении 1950 атмосфер.
KE‾=32kT\overline{\text{KE}} = \frac{3}{2}\text{kT}KE=23kT
.
Обратите внимание, что это уравнение не выглядело бы так элегантно, если бы вместо него использовалась шкала Фаренгейта.
Шкала Кельвина
Кельвин (или «абсолютная температура») является стандартной термодинамической единицей измерения температуры. Это одна из семи основных единиц Международной системы единиц (СИ), и ей присвоен символ единицы K. По международному соглашению единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой Венского стандарта. Средняя океанская вода (вода с определенной смесью изотопов водорода и кислорода). Абсолютный ноль, самая низкая возможная температура, определяется точно как 0 K и -273,15 ° C. Тройная точка воды определяется точно как 273,16 К и 0,01 °С.
Лицензии и ссылки
Контент под лицензией CC, совместно используемый ранее
- Курирование и пересмотр.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретная атрибуция
- идеальный газ. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Закон об идеальном газе. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Номер Авогадро. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- моль. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- идеальный газ.
 Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/ideal_gas. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/ideal_gas. Лицензия : CC BY-SA: Attribution-ShareAlike - Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- адиабатический. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Изотермический процесс. Предоставлено : Википедия.
 Расположен по адресу : https://en.wikipedia.org/wiki/Isothermal_process. Лицензия : CC BY: Attribution
Расположен по адресу : https://en.wikipedia.org/wiki/Isothermal_process. Лицензия : CC BY: Attribution - Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Изобарический процесс. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- первый закон термодинамики. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Удельная теплоемкость. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе.
 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[электронная почта защищена]. Лицензия : CC BY: Attribution
4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[электронная почта защищена]. Лицензия : CC BY: Attribution - Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- идеальный газ. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/ideal_gas. Лицензия : CC BY-SA: Attribution-ShareAlike
- Закон об идеальном газе.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Проект бесплатных научных текстов для старших классов, тепловые свойства и идеальные газы: закон идеального газа и общее уравнение газа. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Изотермический процесс.
 Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
Предоставлено : Википедия. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Шина. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Броуновское движение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Константа Авогадро. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Броуновское движение. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Постоянная Фарадея. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- газовая постоянная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Isothermal_process. Лицензия : CC BY: Attribution
- Изотермический процесс.
 Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
Предоставлено : Википедия. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Шина. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Авогадро Амедео. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- абсолютный ноль. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Термодинамическая температура. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Международная система единиц.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Венский стандарт среднего значения морской воды. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Изотермический процесс. Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.
 org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Лицензия : CC BY: Attribution - Шина. Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
- Авогадро Амедео. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/File:Avogadro_Amedeo.jpg. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Температура. 28 апреля 2014 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Кинетическая теория. Предоставлено : Википедия. Лицензия : Общественное достояние: Неизвестно Авторские права
Вопрос Видео: Расчет работы, затраченной на сжатие идеального газа
Стенограмма видео
Цилиндр с подвижной крышкой
содержит воздух объемом 0,042 кубических метра при давлении 101 кПа. Крышка цилиндра опущена вниз
внешней силой 𝐅, как показано на схеме. Сила включает в себя крышку
масса. В результате крышка опускается.
на 10 сантиметров, а давление воздуха увеличивается на 28 килопаскалей. Затем крышка перестает двигаться, когда
давление над ним и под ним выравнивается. Давление изменяется линейно как
крышка двигается и температура воздуха не меняется во время
сжатие. Какую работу совершили, чтобы сжать
газ? Дайте ответ ближайшему
джоуль.
Крышка цилиндра опущена вниз
внешней силой 𝐅, как показано на схеме. Сила включает в себя крышку
масса. В результате крышка опускается.
на 10 сантиметров, а давление воздуха увеличивается на 28 килопаскалей. Затем крышка перестает двигаться, когда
давление над ним и под ним выравнивается. Давление изменяется линейно как
крышка двигается и температура воздуха не меняется во время
сжатие. Какую работу совершили, чтобы сжать
газ? Дайте ответ ближайшему
джоуль.
Этот вопрос просит нас найти работу, совершаемую над крышкой этого цилиндра с воздухом. Есть о чем подумать в этот вопрос. Начнем с того, что разберем все информацию, которую нам предоставили. И тогда мы можем решить, что метод, который мы собираемся использовать, чтобы найти ответ.
Для начала у нас есть цилиндр
содержащий воздух объемом 0,042 м3 при давлении 101
килопаскалей. Это первоначальная настройка перед
крышка цилиндра движется. Поэтому мы обозначим эти количества 𝑉
один и 𝑃 один. Нам также говорят, что есть 101
килопаскалей атмосферного давления, которые мы обозначим 𝑃 sub a. Первоначально давление газа
в цилиндре равно атмосферному давлению, а это означает, что крышка не
шаг.
Это первоначальная настройка перед
крышка цилиндра движется. Поэтому мы обозначим эти количества 𝑉
один и 𝑃 один. Нам также говорят, что есть 101
килопаскалей атмосферного давления, которые мы обозначим 𝑃 sub a. Первоначально давление газа
в цилиндре равно атмосферному давлению, а это означает, что крышка не
шаг.
Вызов формулы для
давление. Давление равно силе
деленная на площадь, на которую действует сила. Таким образом, равное давление означает, что существует
равной силы от воздуха вне цилиндра, атмосферного давления и от
воздух внутри цилиндра. Это уравновешенные силы, поэтому
крышка не двигается. Тогда внешняя сила 𝐅 равна
прикладывается к крышке цилиндра, заставляя ее сместиться вниз на 10 сантиметров
поскольку силы больше не уравновешены. Есть дополнительный нисходящий
сила. Мы видим, что это вызывает
объем воздуха в цилиндре уменьшается. Мы назовем этот новый том 𝑉
два. Когда крышка опускается, это вызывает
давление воздуха возрастет на 28 кПа. Итак, новое давление в цилиндре
𝑃 два равно начальному давлению 101 килопаскаль плюс 28 килопаскалей. Это равно 129килопаскалей.
Мы видим, что это вызывает
объем воздуха в цилиндре уменьшается. Мы назовем этот новый том 𝑉
два. Когда крышка опускается, это вызывает
давление воздуха возрастет на 28 кПа. Итак, новое давление в цилиндре
𝑃 два равно начальному давлению 101 килопаскаль плюс 28 килопаскалей. Это равно 129килопаскалей.
Мы также знаем, что крышка останавливается движется потому, что давление над ним и под ним уравнивается. Другими словами, крышка останавливается. движется, когда 𝑃 два становится равным сумме атмосферного давления и давление за счет силы 𝐅, которую мы назовем 𝑃 sub F. Мы знаем, что эта сила увеличивает давление газа 28 кПа. Это означает, что сама сила необходимо приложить давление 28 килопаскалей через крышку цилиндра.
Теперь мы поняли настройку,
давайте подумаем над вопросом, который нам задали. Нам нужно найти работу, совершенную
эта сила 𝐅, когда она перемещает крышку вниз. Сила 𝐅 и давление на нее
применяются, связаны формулой 𝑃 sub F равно 𝐅, деленному на 𝐴, где 𝐴 — это
площадь поверхности крышки. Поскольку это сила, которую мы
действительно интересно, давайте изменим это, чтобы сделать 𝐅 предметом. Для этого нам нужно всего лишь
умножьте обе части уравнения на площадь 𝐴. Это дает нам 𝐅 равно 𝑃 sub F
раз 𝐴.
Сила 𝐅 и давление на нее
применяются, связаны формулой 𝑃 sub F равно 𝐅, деленному на 𝐴, где 𝐴 — это
площадь поверхности крышки. Поскольку это сила, которую мы
действительно интересно, давайте изменим это, чтобы сделать 𝐅 предметом. Для этого нам нужно всего лишь
умножьте обе части уравнения на площадь 𝐴. Это дает нам 𝐅 равно 𝑃 sub F
раз 𝐴.
Нам нужно найти работу, выполненную
сила. Напомним, что совершенная работа 𝑊 равна
равна силе, умноженной на расстояние, на которое она действует 𝑑. В этом случае сила действует на
сдвиньте крышку вниз. Итак, 𝑑 равно расстоянию
через который движется крышка, 10 сантиметров. Если мы подставим наше выражение вместо
силу 𝐅 в уравнение для проделанной работы, находим, что проделанная работа равна
давление 𝑃 sub F, умноженное на площадь крышки, умноженное на расстояние, пройденное
крышка. Мы знаем значения давления
𝑃 sub F и расстояние 𝑑, поэтому нам нужно найти площадь 𝐴.
Мы знаем значения давления
𝑃 sub F и расстояние 𝑑, поэтому нам нужно найти площадь 𝐴.
Чтобы найти значение 𝐴, мы просто
нужно использовать простую геометрию. Напомним, что объем
цилиндра равна площади поверхности его круглой грани, умноженной на его
высота. Если мы преобразуем это уравнение в
делаем 𝐴 предметом, находим, что 𝐴 равно объему цилиндра, разделенному
по высоте. Нам не говорят высоту
либо начальный цилиндр газа, либо его высота после перемещения крышки. Однако мы знаем высоту
вот этот воображаемый цилиндр, 10 сантиметров. Мы также знаем, что объем
этот цилиндр, который мы назовем Δ𝑉, равен разности между
начальный объем цилиндра и его конечный объем. Итак, Δ𝑉 равно 𝑉 один минус 𝑉
два. Итак, площадь поверхности цилиндра
Крышка должна быть равна 𝑉 один минус 𝑉 два, деленное на расстояние 𝑑.
Теперь вернемся к уравнению за работу, совершенную силой. Если мы подставим в наше выражение для 𝐴 мы находим, что проделанная работа равна давлению 𝑃 sub F, умноженному на изменение объема разделить на 𝑑 умножить на 𝑑. Мы видим, что эти факторы 𝑑 отменить, что упрощает выражение до 𝑊 равно давлению 𝑃 меньше F раз 𝑉 один минус 𝑉 два.
Теперь осталось только
вычислить значение 𝑉 два. Напомним, что для газа постоянной
массы, мы можем использовать формулу 𝑃 один 𝑉 один разделить на 𝑇 один равно 𝑃 два 𝑉 два
разделить на 𝑇 два, где величины, отмеченные единицей, относятся к
начальное состояние, а величины, отмеченные цифрой двойка, относятся к конечному состоянию газа.
государство. Нам говорят, что когда газ
сжимается, его температура не меняется. Это означает, что 𝑇 единица равна 𝑇
два, и мы можем исключить их из наших уравнений. Это оставляет нас с 𝑃 один раз 𝑉
один равен 𝑃 два раза 𝑉 два. Мы можем изменить это, чтобы сделать 𝑉
два субъекта, разделив обе части уравнения на 𝑃 два. Отсюда мы находим, что 𝑉 два равно
равно 𝑃 один раз 𝑉 один разделить на 𝑃 два.
Это оставляет нас с 𝑃 один раз 𝑉
один равен 𝑃 два раза 𝑉 два. Мы можем изменить это, чтобы сделать 𝑉
два субъекта, разделив обе части уравнения на 𝑃 два. Отсюда мы находим, что 𝑉 два равно
равно 𝑃 один раз 𝑉 один разделить на 𝑃 два.
Теперь нам просто нужно подставить ценности, которые мы нашли в начале нашей работы. 𝑃 один равен 101 килопаскалю, 𝑉 один равен 0,042 кубометра, а 𝑃 два равен 129 кПа. Если мы закончим расчет, то найти, что 𝑉 два равно 0,03288 кубических метров.
Наконец, мы готовы к расчету
значение работы, совершаемой силой. 𝑊 равно давлению 𝑃 sub
F умножить на 𝑉 один минус 𝑉 два. Для преобразования давления из
килопаскалей в единицу СИ паскалей, мы просто умножаем на 1000, что дает нам 𝑃 sub F
равняется 28000 паскалей. Мы также знаем, что 𝑉 единица равна 0,042.
кубических метров и 𝑉 два равно 0,03288 кубических метров.

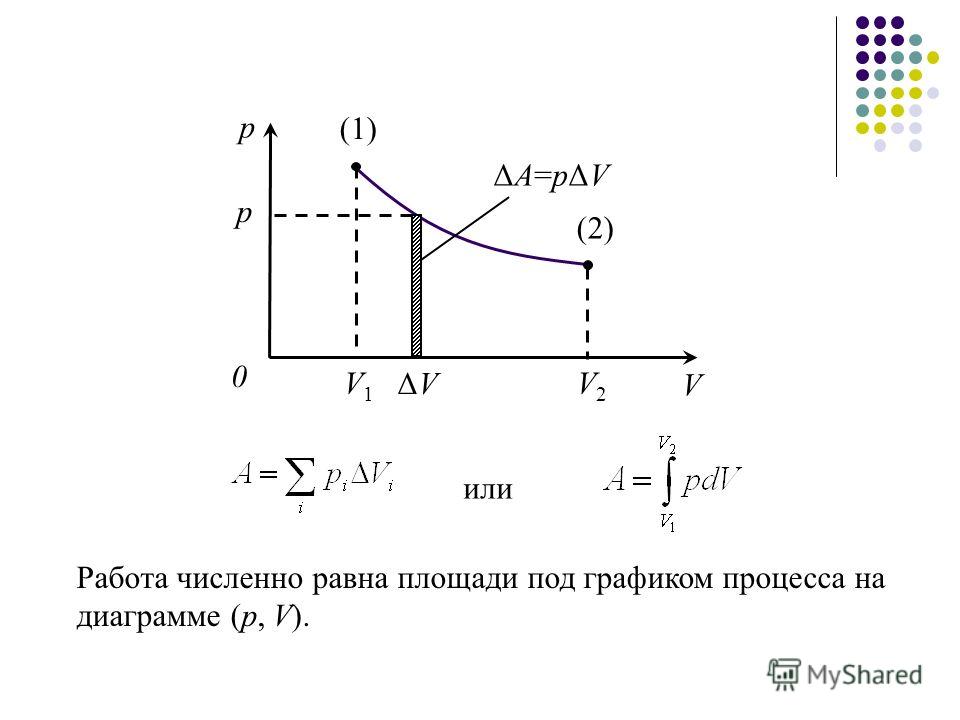 3 Законы сохранения
3 Законы сохранения СТО
СТО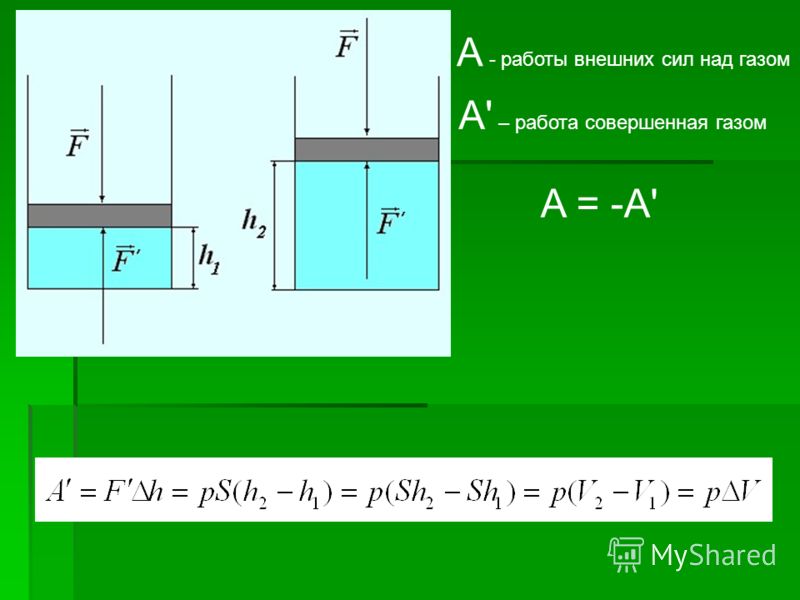

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

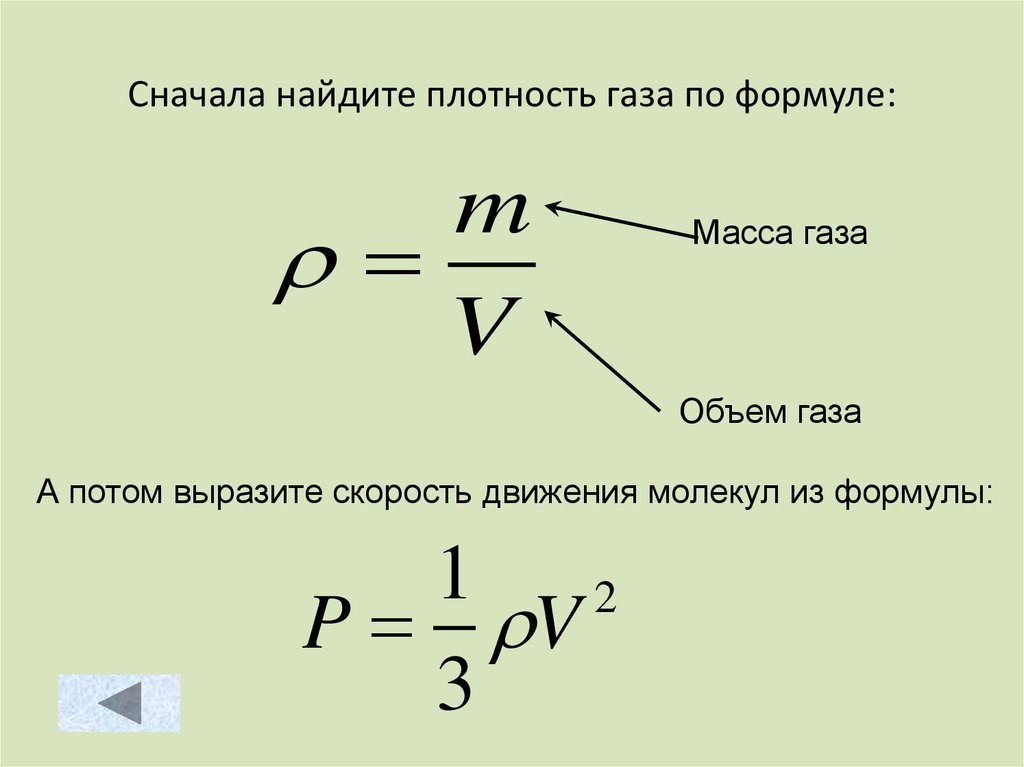
 Следовательно, теплоемкость идеального газа стремится к бесконечности:
Следовательно, теплоемкость идеального газа стремится к бесконечности: На значение удельной теплоёмкости влияет температура вещества. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C.
На значение удельной теплоёмкости влияет температура вещества. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C. 4) по T (p=const), получаем
4) по T (p=const), получаем Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы.
Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы.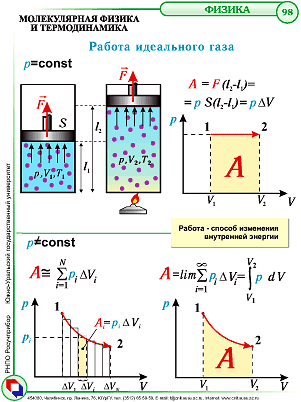
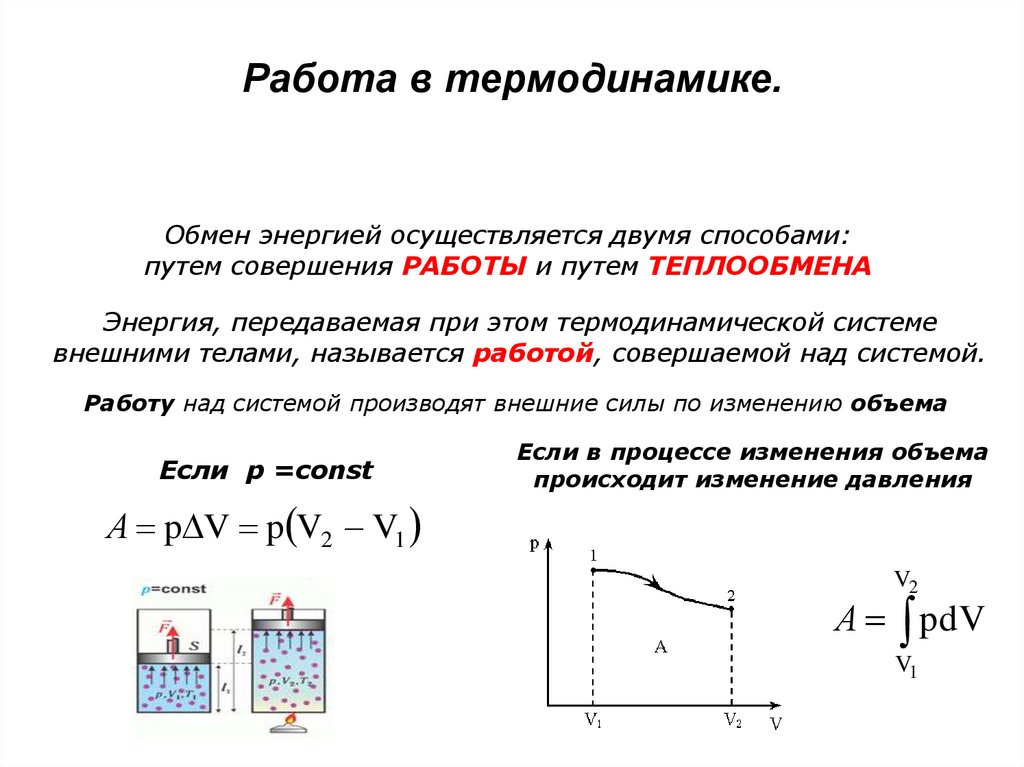
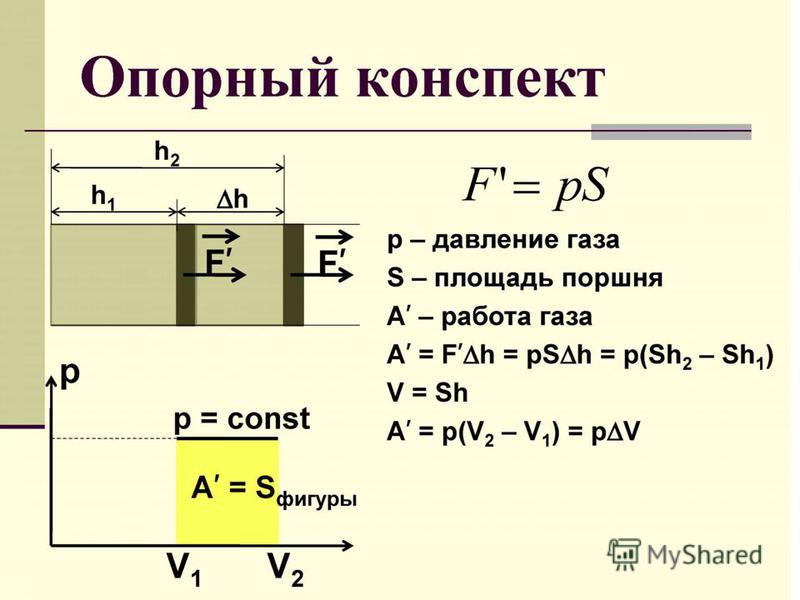 Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.
Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.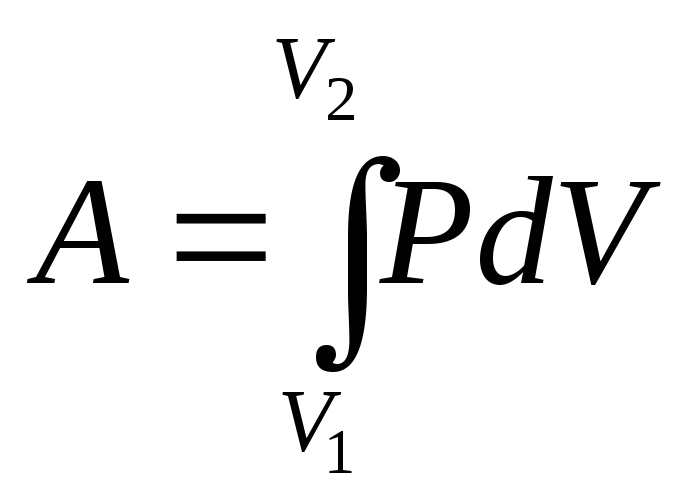
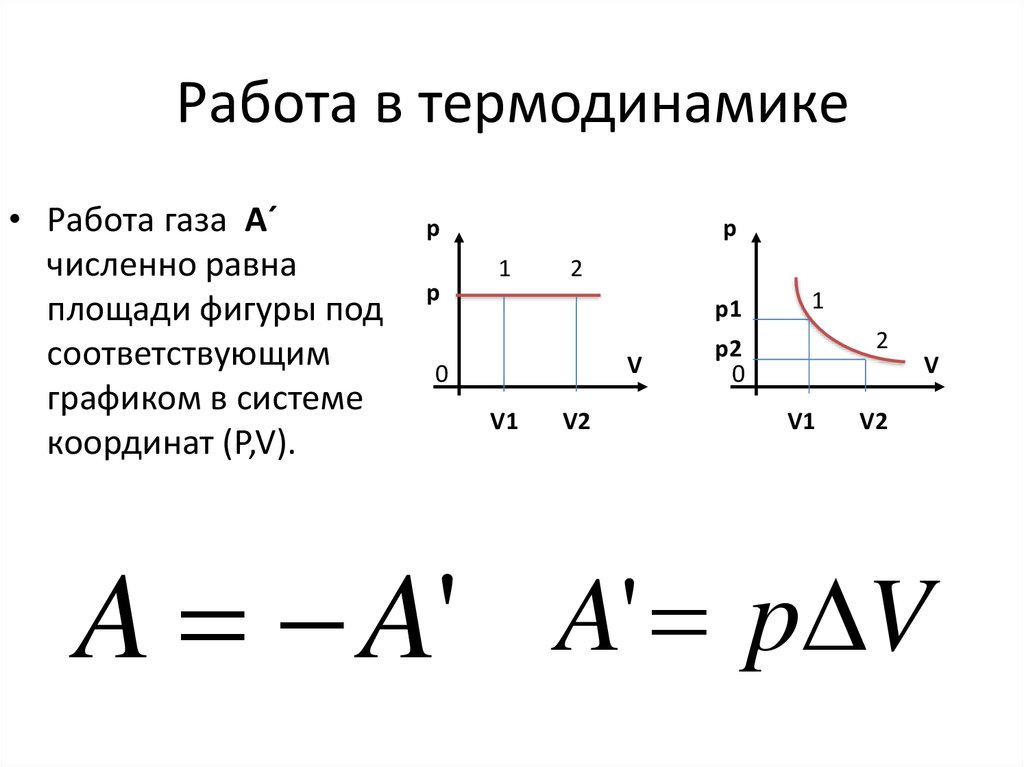 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.011 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.011 с.) В аэродинамике мы больше всего
интересует термодинамика
потоки с высокой скоростью, а в
двигательные установки
которые создают тягу за счет
ускоряющий газ. Чтобы понять, как создается тяга, полезно
изучать основы термодинамики газов.
В аэродинамике мы больше всего
интересует термодинамика
потоки с высокой скоростью, а в
двигательные установки
которые создают тягу за счет
ускоряющий газ. Чтобы понять, как создается тяга, полезно
изучать основы термодинамики газов. Термодинамика помогает нам определить объем работы
и количество теплоты, необходимое для изменения состояния газа. Обратите внимание, что в этом примере у нас есть фиксированная масса газа. Мы можем
поэтому постройте либо
физический том
или
удельный объем, объем, деленный на массу,
так как изменение одинаково для постоянной массы. На фигуре,
мы используем физический том.
Термодинамика помогает нам определить объем работы
и количество теплоты, необходимое для изменения состояния газа. Обратите внимание, что в этом примере у нас есть фиксированная масса газа. Мы можем
поэтому постройте либо
физический том
или
удельный объем, объем, деленный на массу,
так как изменение одинаково для постоянной массы. На фигуре,
мы используем физический том.  Как правило, при изменении состояния громкость
и изменение давления. Поэтому правильнее определить работу как
интегрированное или суммированное переменное давление, умноженное на изменение объема
из состояния 1 в состояние 2. Если мы используем символ S [ ] ds для интеграла, тогда:
Как правило, при изменении состояния громкость
и изменение давления. Поэтому правильнее определить работу как
интегрированное или суммированное переменное давление, умноженное на изменение объема
из состояния 1 в состояние 2. Если мы используем символ S [ ] ds для интеграла, тогда: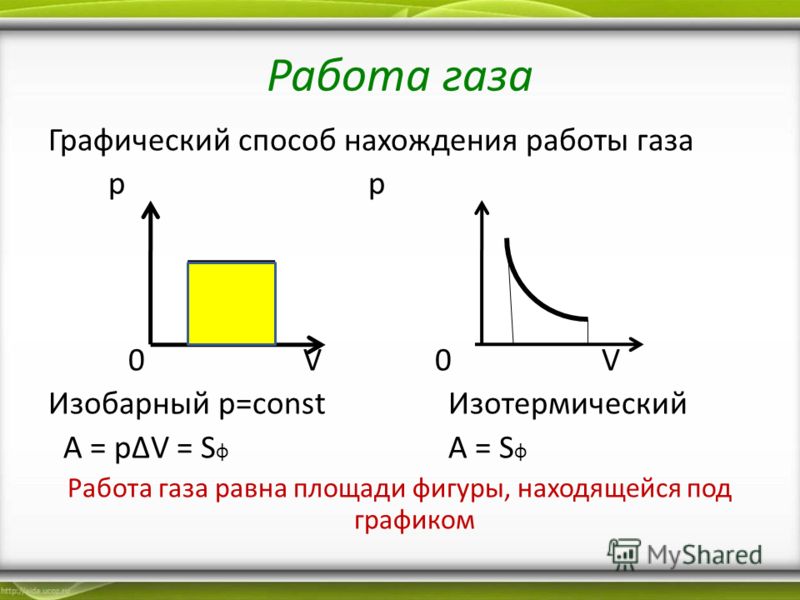 Линия
изогнута, а количество работы, проделанной над газом, показано красным
заштрихованная область ниже этой кривой. Однако мы могли бы перейти из состояния 1
в состояние 2, удерживая
постоянное давление и увеличение объема на
нагревание газа по закону Шарля.
результирующее изменение состояния происходит из состояния 1 в промежуточное
Обозначьте «а» на графике. Состояние «а» находится под тем же давлением, что и состояние 1,
но с другой громкостью. Если мы затем удалим веса, удерживая
постоянного объема, мы переходим к состоянию 2. Работа, выполненная в этом
процесс показан желтой заштрихованной областью. Используя либо процесс меняем состояние газа с State 1 на State
2. Но работа для
процесс при постоянном давлении больше, чем работа при криволинейном
линейный процесс. Работа, совершаемая газом, зависит не только от начального
и конечные состояния газа, но и процесс, используемый для изменения
штат. Различные процессы могут создавать одно и то же состояние, но
производят разный объем работы.
Линия
изогнута, а количество работы, проделанной над газом, показано красным
заштрихованная область ниже этой кривой. Однако мы могли бы перейти из состояния 1
в состояние 2, удерживая
постоянное давление и увеличение объема на
нагревание газа по закону Шарля.
результирующее изменение состояния происходит из состояния 1 в промежуточное
Обозначьте «а» на графике. Состояние «а» находится под тем же давлением, что и состояние 1,
но с другой громкостью. Если мы затем удалим веса, удерживая
постоянного объема, мы переходим к состоянию 2. Работа, выполненная в этом
процесс показан желтой заштрихованной областью. Используя либо процесс меняем состояние газа с State 1 на State
2. Но работа для
процесс при постоянном давлении больше, чем работа при криволинейном
линейный процесс. Работа, совершаемая газом, зависит не только от начального
и конечные состояния газа, но и процесс, используемый для изменения
штат. Различные процессы могут создавать одно и то же состояние, но
производят разный объем работы.
 Энергия передается воздуху за счет тепла из-за сопротивления воздуха.
Энергия передается воздуху за счет тепла из-за сопротивления воздуха.