Методы регрессии — CoderLessons.com
Регрессия – это статистический метод, который помогает квалифицировать отношения между взаимосвязанными экономическими переменными. Первый шаг включает в себя оценку коэффициента независимой переменной, а затем измерение достоверности оцененного коэффициента. Это требует формулирования гипотезы, и на основе гипотезы мы можем создать функцию.
Если менеджер хочет определить взаимосвязь между рекламными расходами фирмы и доходами от продаж, он подвергнется проверке гипотезы. Предполагая, что более высокие расходы на рекламу приводят к увеличению продаж для фирмы. Менеджер собирает данные о расходах на рекламу и о выручке от продаж за определенный период времени. Эта гипотеза может быть переведена в математическую функцию, где она приводит к –
Y = A + Bx
Где Y – продажи, x – расходы на рекламу, A и B – постоянные.
После перевода гипотезы в функцию основание для этого должно найти связь между зависимой и независимой переменными. Значение зависимой переменной имеет наибольшее значение для исследователей и зависит от значения других переменных. Независимая переменная используется для объяснения изменения зависимой переменной. Это может быть классифицировано в два типа –
Значение зависимой переменной имеет наибольшее значение для исследователей и зависит от значения других переменных. Независимая переменная используется для объяснения изменения зависимой переменной. Это может быть классифицировано в два типа –
Простая регрессия – одна независимая переменная
Множественная регрессия – несколько независимых переменных
Простая регрессия
Ниже приведены шаги для построения регрессионного анализа –
- Укажите модель регрессии
- Получить данные о переменных
- Оценить количественные отношения
- Проверьте статистическую значимость результатов
- Использование результатов в принятии решений
Формула для простой регрессии –
Y = a + bX + u
Y = зависимая переменная
X = независимая переменная
а = перехват
б = уклон
и = случайный фактор
Данные поперечного сечения предоставляют информацию о группе объектов в данный момент времени, тогда как данные временных рядов предоставляют информацию об одном объекте с течением времени. Когда мы оцениваем уравнение регрессии, оно включает в себя процесс определения наилучшей линейной зависимости между зависимой и независимой переменными.
Когда мы оцениваем уравнение регрессии, оно включает в себя процесс определения наилучшей линейной зависимости между зависимой и независимой переменными.
Метод обыкновенных наименьших квадратов (OLS)
Обычный метод наименьших квадратов предназначен для подгонки линии через разброс точек таким образом, чтобы сумма квадратов отклонений точек от линии сводилась к минимуму. Это статистический метод. Обычно программные пакеты выполняют оценку OLS.
Y = a + bX
Коэффициент определения (R
2 )Коэффициент детерминации – это мера, которая показывает процент изменения зависимой переменной из-за изменений в независимых переменных. R 2 является показателем качества модели соответствия. Ниже приведены методы –
Общая сумма квадратов (TSS)
Сумма квадратов отклонений значений выборки Y от среднего значения Y.
TSS = SUM (Y i – Y) 2
Y i = зависимые переменные
Y = среднее значение зависимых переменных
я = количество наблюдений
Регрессия Сумма квадратов (RSS)
Сумма квадратов отклонений расчетных значений Y от среднего значения Y.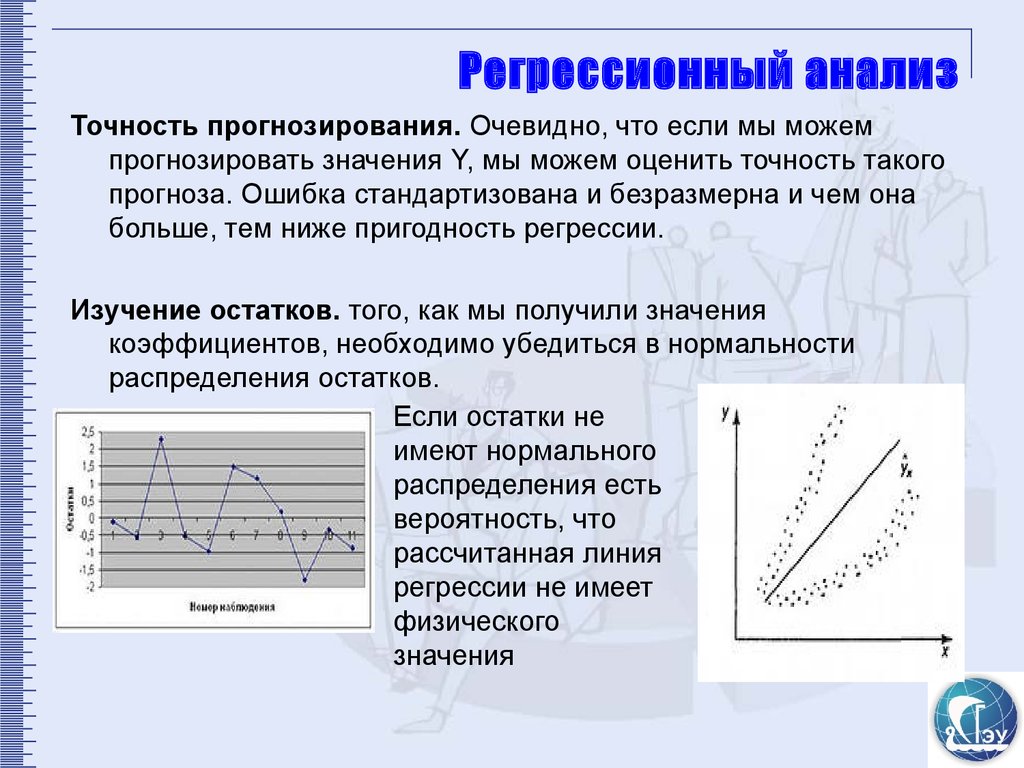
RSS = СУММА (Ỷ i – uY) 2
Ỷ i = оценочное значение Y
Y = среднее значение зависимых переменных
я = количество вариантов
Ошибка суммы квадратов (ESS)
Сумма квадратов отклонений выборочных значений Y от расчетных значений Y.
ESS = СУММА (Y i – Ỷ i ) 2
Ỷ i = оценочное значение Y
Y i = зависимые переменные
я = количество наблюдений
R2 =
RSS / TSS
= 1 –
ESS / TSS
R 2 измеряет долю общего отклонения Y от его среднего значения, что объясняется регрессионной моделью. Чем ближе R 2 к единице, тем больше объясняющая сила уравнения регрессии. Значение R 2, близкое к 0, указывает на то, что уравнение регрессии будет иметь очень мало объяснительной силы.
Для оценки коэффициентов регрессии используется выборка из совокупности, а не всей совокупности.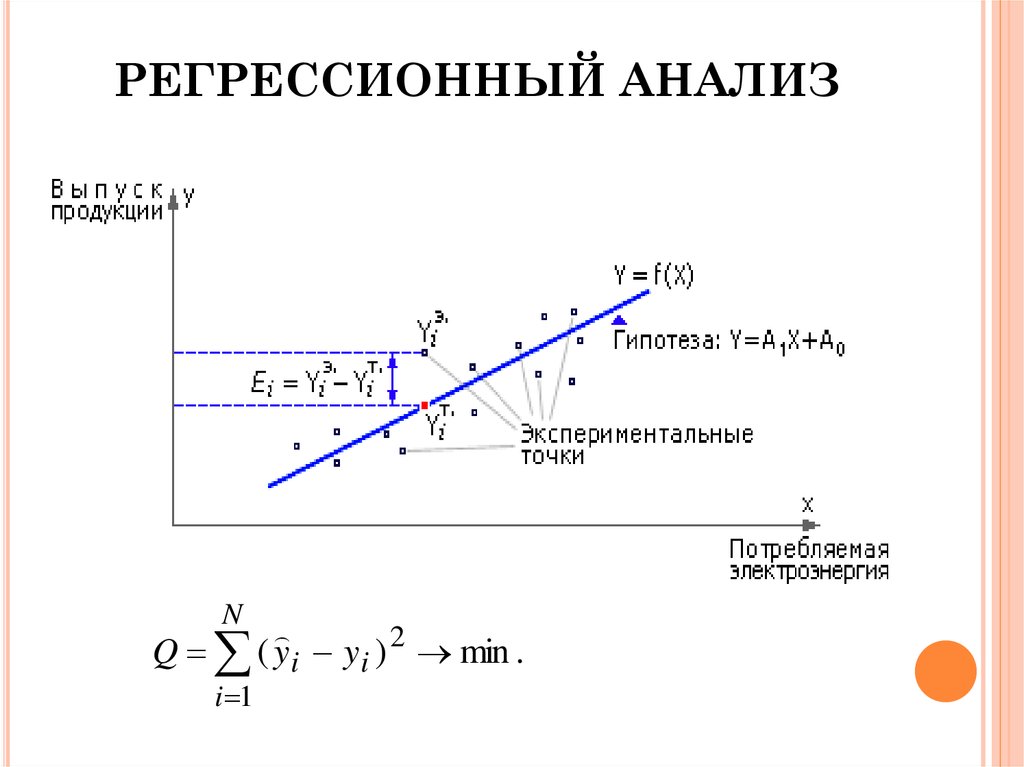
Оценка коэффициентов регрессии
Каждая выборка из населения генерирует свой собственный перехват. Для расчета статистической разницы можно использовать следующие методы:
Двуххвостый тест –
Нулевая гипотеза: H 0 : b = 0
Альтернативная гипотеза: H a : b ≠ 0
Один хвостатый тест –
Нулевая гипотеза: H 0 : b> 0 (или b <0)
Альтернативная гипотеза: H a : b <0 (или b> 0)
Статистический тест –
т =
(b – E (b)) / SE b
б = расчетный коэффициент
E (b) = b = 0 (нулевая гипотеза)
SE b = стандартная ошибка коэффициента
,
Значение t зависит от степени свободы, одного или двух неудачных испытаний и уровня значимости.
Множественный регрессионный анализ
В отличие от простой регрессии в множественном регрессионном анализе, коэффициенты указывают на изменение зависимых переменных, предполагая, что значения других переменных постоянны.
Тест статистической значимости называется F-тестом . F-тест полезен, поскольку он измеряет статистическую значимость всего уравнения регрессии, а не только для отдельного человека. Здесь В нулевой гипотезе нет никакой связи между зависимой переменной и независимыми переменными совокупности.
Формула – H 0 : b1 = b2 = b3 =…. = bk = 0
Не существует никакой связи между зависимой переменной и k независимыми переменными для совокупности.
F-тест статический –
F= frac left( fracR2K right) frac(1−R2)(nk−1)
Критическое значение F зависит от числителя и знаменателя, степени свободы и уровня значимости. F-таблица может быть использована для определения критического значения F. По сравнению с F – значением с критическим значением (F *) –
Если F> F *, нам нужно отвергнуть нулевую гипотезу.
Если F <F *, не отклоняйте нулевую гипотезу, так как нет существенной связи между зависимой переменной и всеми независимыми переменными.
Линейная регрессия | BaseGroup Labs
Назначение
Линейная регрессия предназначена для получения прогноза непрерывных числовых переменных. Кроме того, реализованный в аналитической платформе Deductor доработанный вариант линейной регрессии позволяет также решать и задачу классификации.
Достоинства линейной регрессии:
- Скорость и простота получения модели.
- Интерпретируемость модели. Линейная модель является прозрачной и понятной для аналитика.
 По полученным коэффициентам регрессии можно судить о том, как тот или иной фактор влияет на результат, сделать на этой основе дополнительные полезные выводы.
По полученным коэффициентам регрессии можно судить о том, как тот или иной фактор влияет на результат, сделать на этой основе дополнительные полезные выводы. - Широкая применимость. Большое количество реальных процессов в экономике и бизнесе можно с достаточной точностью описать линейными моделями.
- Изученность данного подхода. Для линейной регрессии известны типичные проблемы (например, мультиколлинеарность) и их решения, разработаны и реализованы тесты оценки статической значимости получаемых моделей.
Примеры применения
Анализ эластичности спроса по цене, характеризующей реакцию потребительского спроса на изменение цены товара. Обработчик позволяет построить модель продаж, где в качестве входной переменной будет использоваться цена, а в качестве выходной – объем продаж.
Прогнозирования объема продаж. Регрессия строится на основе временного ряда продаж за репрезентативный период. Данная модель является базисом для формирования оптимального плана закупок и товарно-финансовых планов.
Прогнозирование стоимости ценных бумаг. Регрессионная модель строится на основе таких показателей, как чистая прибыль компании, доход, рентабельность выручки компании, балансовой стоимости и прочее.
Прогнозирование загруженности веб-сервиса. Резкие всплески интереса могут повысить нагрузку на серверы и отрицательно сказаться на качестве работы веб-сервиса. Эта задача особенно актуальная, если вычислительные ресурсы арендуются в облаке, где имеется возможность гибко управлять мощностями доступных серверов.
Описание алгоритма
Регрессия – это условное математическое ожидание непрерывной зависимой (выходной) переменной при наблюдаемых значениях независимых (входных) переменных. Линейная регрессия основана на гипотезе, что искомая зависимость – линейная. Каждая независимая переменная вносит аддитивный вклад в результирующее значение с некоторым весом, называемом коэффициентом регрессии.
Регрессия называется простой, если входная переменная одна. Однако такая модель является слишком грубым приближением действительности, и на практике, как правило, интересны зависимости от нескольких переменных (множественная регрессия).
Однако такая модель является слишком грубым приближением действительности, и на практике, как правило, интересны зависимости от нескольких переменных (множественная регрессия).
Построение линейной регрессии заключается в расчете её коэффициентов методом наименьших квадратов.
Несмотря на свою универсальность, линейная регрессионная модель не всегда пригодна для качественного предсказания зависимой переменной. Например, если выходная переменная является категориальной или бинарной, приходится использовать различные модификации регрессии.
Одной из таких модификаций является логистическая регрессия, предназначенная для оценки вероятности того, что зависимая переменная примет значение от 0 до 1.
Множественная линейная регрессия (MLR) Определение, формула и пример
Что такое множественная линейная регрессия (MLR)?
Множественная линейная регрессия (MLR), также известная как множественная регрессия, представляет собой статистический метод, который использует несколько независимых переменных для прогнозирования результата переменной отклика.
Ключевые выводы
- Множественная линейная регрессия (MLR), также известная как множественная регрессия, представляет собой статистический метод, использующий несколько независимых переменных для прогнозирования результата переменной отклика.
- Множественная регрессия — это расширение линейной (OLS) регрессии, в котором используется только одна независимая переменная.
- MLR широко используется в эконометрике и финансовых выводах.
Формула и расчет множественной линейной регрессии
у я «=» β 0 + β 1 Икс я 1 + β 2 Икс я 2 + . . . + β п Икс я п + ϵ где, для я «=» н наблюдения: у я «=» зависимая переменная Икс я «=» пояснительные переменные β 0 «=» y-перехват (постоянный термин) β п «=» коэффициенты наклона для каждой независимой переменной ϵ «=» член ошибки модели (также известный как остатки) \begin{align}&y_i = \beta_0 + \beta _1 x_{i1} + \beta _2 x_{i2} + .
О чем может рассказать множественная линейная регрессия
Простая линейная регрессия — это функция, которая позволяет аналитику или статистику делать прогнозы относительно одной переменной на основе информации, известной о другой переменной. Линейную регрессию можно использовать только при наличии двух непрерывных переменных — независимой переменной и зависимой переменной. Независимая переменная — это параметр, который используется для вычисления зависимой переменной или результата. Модель множественной регрессии распространяется на несколько независимых переменных.
Независимая переменная — это параметр, который используется для вычисления зависимой переменной или результата. Модель множественной регрессии распространяется на несколько независимых переменных.
Модель множественной регрессии основана на следующих предположениях:
- Существует линейная зависимость между зависимыми переменными и независимыми переменными
- Независимые переменные не слишком сильно коррелируют друг с другом
- y i наблюдения выбираются независимо и случайным образом из совокупности
- Остатки должны быть нормально распределены со средним значением 0 и дисперсией σ
Коэффициент детерминации (R-квадрат) — это статистическая метрика, которая используется для измерения того, какая часть вариации результата может быть объяснена вариацией независимых переменных. R 2 всегда увеличивается по мере того, как в модель MLR добавляется больше предикторов, даже если предикторы могут быть не связаны с переменной результата.
Таким образом, R 2 сам по себе не может использоваться для определения того, какие предикторы следует включить в модель, а какие следует исключить. р 2 может принимать значения только от 0 до 1, где 0 означает, что результат не может быть предсказан ни одной из независимых переменных, а 1 означает, что результат может быть предсказан без ошибок на основе независимых переменных.
При интерпретации результатов множественной регрессии бета-коэффициенты действительны при условии, что все остальные переменные остаются постоянными («все остальные равны»). Выходные данные множественной регрессии могут отображаться горизонтально в виде уравнения или вертикально в виде таблицы.
Пример использования множественной линейной регрессии
Например, аналитик может захотеть узнать, как движение рынка влияет на цену ExxonMobil (XOM). В этом случае их линейное уравнение будет иметь значение индекса S&P 500 в качестве независимой переменной, или предиктора, и цену XOM в качестве зависимой переменной.
На самом деле исход события предсказывают многочисленные факторы. Движение цен ExxonMobil, например, зависит не только от общего состояния рынка. Другие предикторы, такие как цена на нефть, процентные ставки и динамика цен на нефтяные фьючерсы, могут влиять на цену XOM и цены акций других нефтяных компаний. Чтобы понять взаимосвязь, в которой присутствует более двух переменных, используется множественная линейная регрессия.
Множественная линейная регрессия (MLR) используется для определения математической взаимосвязи между несколькими случайными величинами. Другими словами, MLR исследует, как несколько независимых переменных связаны с одной зависимой переменной. Как только каждый из независимых факторов определен для прогнозирования зависимой переменной, информация о нескольких переменных может быть использована для создания точного прогноза уровня их влияния на результирующую переменную. Модель создает зависимость в виде прямой линии (линейной), которая наилучшим образом соответствует всем отдельным точкам данных.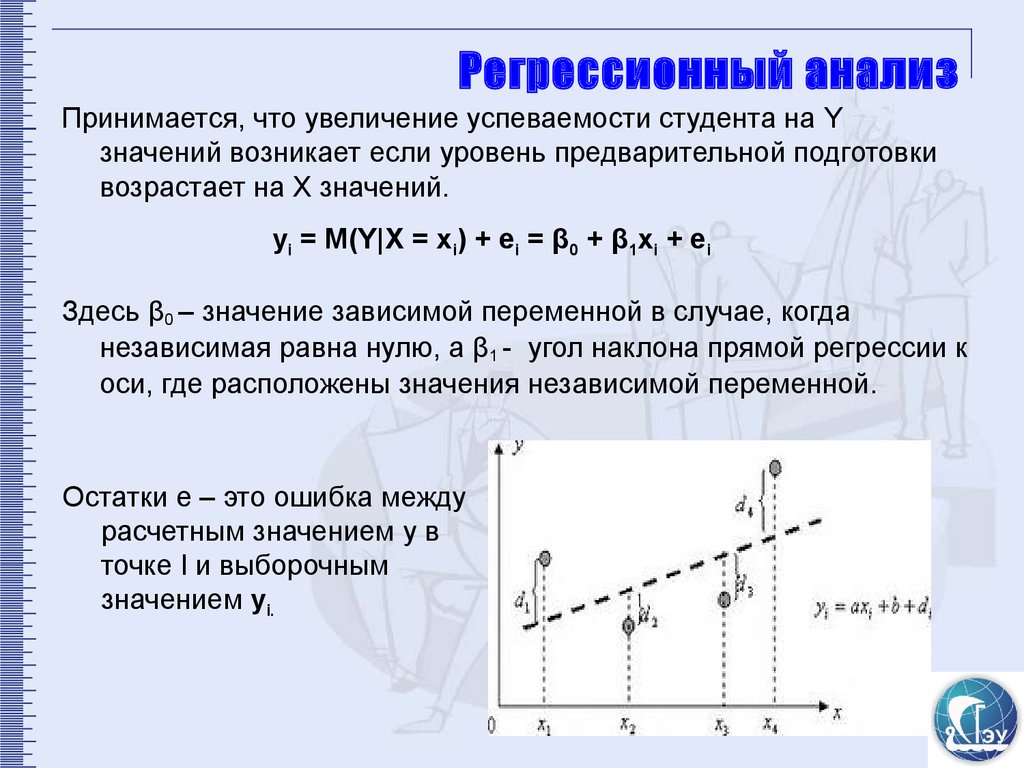
Ссылаясь на приведенное выше уравнение MLR, в нашем примере:
- y i = зависимая переменная — цена XOM
- x i1 = процентные ставки
- x i2 = цена на нефть
- x i3 = значение индекса S&P 500
- x i4 = цена фьючерса на нефть
- B 0 = пересечение оси Y в нулевое время
- B 1 = коэффициент регрессии, который измеряет единичное изменение зависимой переменной, когда x i1 changes — изменение цены XOM при изменении процентных ставок
- B 2 = значение коэффициента, измеряющего единичное изменение зависимой переменной при изменении x i2 — изменение цены XOM при изменении цен на нефть
Оценки методом наименьших квадратов — B 0 , B 1 , B 2 … B p — обычно вычисляются с помощью статистического программного обеспечения. Сколько переменных может быть включено в регрессионную модель, в которой каждая независимая переменная дифференцируется числом — 1,2, 3, 4. ..p. Модель множественной регрессии позволяет аналитику прогнозировать результат на основе информации, предоставленной несколькими независимыми переменными.
..p. Модель множественной регрессии позволяет аналитику прогнозировать результат на основе информации, предоставленной несколькими независимыми переменными.
Тем не менее, модель не всегда идеально точна, поскольку каждая точка данных может немного отличаться от результата, предсказанного моделью. Остаточное значение E, представляющее собой разницу между фактическим результатом и прогнозируемым результатом, включено в модель для учета таких незначительных отклонений.
Предположим, что мы запускаем нашу модель ценовой регрессии XOM через программное обеспечение для расчета статистики, которое возвращает следующий результат:
Изображение Сабрины Цзян © Investopedia 2020 Аналитик интерпретировал бы этот результат как означающий, что если другие переменные остаются постоянными, цена XOM увеличится на 7,8%, если цена на нефть на рынках увеличится на 1%. Модель также показывает, что цена XOM снизится на 1,5% после повышения процентных ставок на 1%. р 2 указывает, что 86,5% колебаний курса акций Exxon Mobil можно объяснить изменениями процентной ставки, цен на нефть, нефтяных фьючерсов и индекса S&P 500.
Разница между линейной и множественной регрессией
Регрессия с помощью обычных линейных квадратов (OLS) сравнивает реакцию зависимой переменной на изменение некоторых независимых переменных. Однако зависимая переменная редко объясняется только одной переменной. В этом случае аналитик использует множественную регрессию, которая пытается объяснить зависимую переменную, используя более одной независимой переменной. Множественные регрессии могут быть линейными и нелинейными.
Множественные регрессии основаны на предположении, что между зависимыми и независимыми переменными существует линейная связь. Он также предполагает отсутствие значительной корреляции между независимыми переменными.
Что делает множественную регрессию множественной?
Множественная регрессия рассматривает влияние более чем одной объясняющей переменной на некоторый интересующий результат. Он оценивает относительное влияние этих объясняющих или независимых переменных на зависимую переменную, когда все остальные переменные в модели остаются постоянными.
Зачем использовать множественную регрессию вместо простой регрессии МНК?
Зависимая переменная редко объясняется только одной переменной. В таких случаях аналитик использует множественную регрессию, которая пытается объяснить зависимую переменную, используя более одной независимой переменной. Модель, однако, предполагает, что между независимыми переменными нет серьезных корреляций.
Можно ли выполнить множественную регрессию вручную?
Маловероятно, поскольку модели множественной регрессии сложны и становятся еще более сложными, когда в модель включается больше переменных или когда увеличивается объем данных для анализа. Для выполнения множественной регрессии вам, вероятно, потребуется использовать специализированное статистическое программное обеспечение или функции в таких программах, как Excel.
Что означает линейность множественной регрессии?
При множественной линейной регрессии модель вычисляет линию наилучшего соответствия, которая минимизирует дисперсии каждой из включенных переменных по отношению к зависимой переменной. Поскольку он соответствует линии, это линейная модель. Существуют также модели нелинейной регрессии с несколькими переменными, такие как логистическая регрессия, квадратичная регрессия и пробит-модели.
Поскольку он соответствует линии, это линейная модель. Существуют также модели нелинейной регрессии с несколькими переменными, такие как логистическая регрессия, квадратичная регрессия и пробит-модели.
Как модели множественной регрессии используются в финансах?
Любая эконометрическая модель, учитывающая более одной переменной, может быть кратной. Факторные модели сравнивают два или более факторов для анализа взаимосвязей между переменными и результирующей производительностью. Фама и французский трехфакторный мод — это такая модель, которая расширяет модель ценообразования капитальных активов (CAPM), добавляя факторы риска размера и риска стоимости к фактору рыночного риска в CAPM (которая сама по себе является регрессионной моделью). Включая эти два дополнительных фактора, модель адаптируется к этой тенденции превосходства, что, как считается, делает ее лучшим инструментом для оценки эффективности менеджера.
Что такое регрессионный анализ? » Учебники по экономике
В эконометрике мы используем инструмент регрессионного анализа, чтобы понять экономические отношения посредством количественной оценки.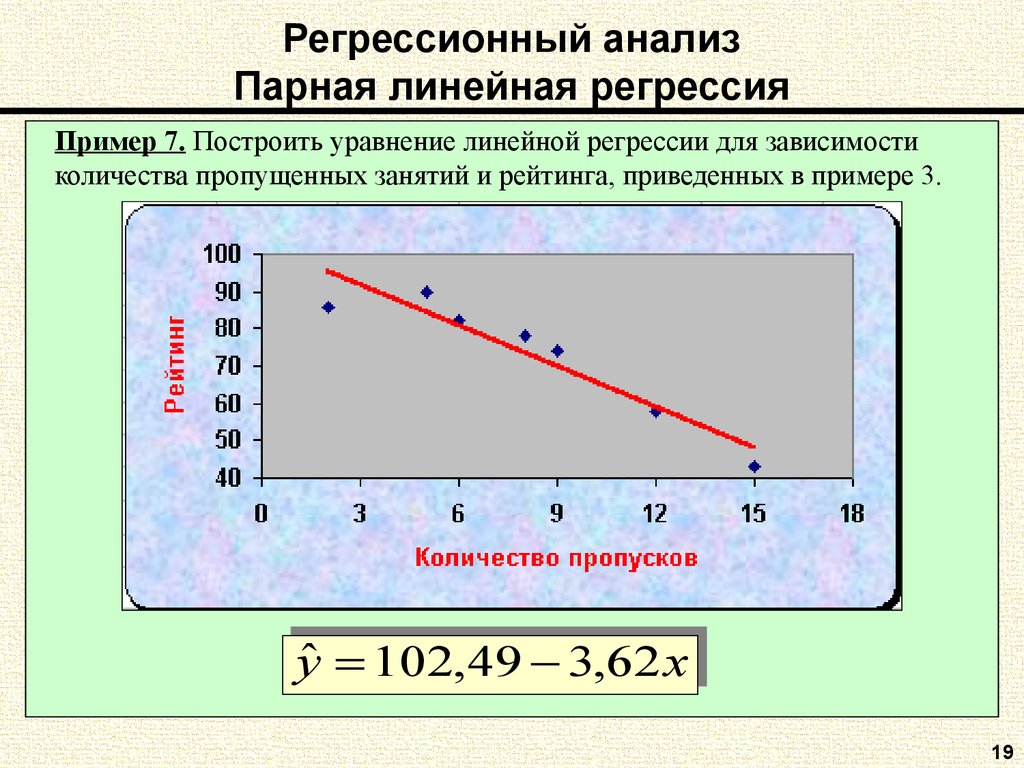 Эта количественная оценка выполняется с помощью регрессии, которая является одним из наиболее частых и важных инструментов, используемых для понимания экономических теорий. Следовательно, легко описать зависимость в теоретической форме, но было бы трудно записать ее в виде уравнения и оценить теорию по заданным данным. Кроме того, мы находим не только взаимосвязь переменных, но и направление и величину изменения переменных, используемых в теории. Таким образом, чтобы предсказать оба фактора: 1) количество изменений 2) направление изменений, а также значимость взаимосвязи между переменными, мы используем регрессионный анализ.
Эта количественная оценка выполняется с помощью регрессии, которая является одним из наиболее частых и важных инструментов, используемых для понимания экономических теорий. Следовательно, легко описать зависимость в теоретической форме, но было бы трудно записать ее в виде уравнения и оценить теорию по заданным данным. Кроме того, мы находим не только взаимосвязь переменных, но и направление и величину изменения переменных, используемых в теории. Таким образом, чтобы предсказать оба фактора: 1) количество изменений 2) направление изменений, а также значимость взаимосвязи между переменными, мы используем регрессионный анализ.
Определение регрессионного анализа
Регрессионный анализ — это статистический метод, который фактически объясняет изменение зависимой переменной из-за движения других независимых переменных.
Это метод предсказания неизвестной переменной через известные переменные.
Зависимая переменная, независимая переменная и причинно-следственная связь в регрессионном анализе:
Зависимая переменная — это переменная, которая зависит от действия независимой переменной. Любые изменения, сделанные в независимой переменной, приведут к изменению зависимой переменной. Это причинно-следственная связь между переменными.
Любые изменения, сделанные в независимой переменной, приведут к изменению зависимой переменной. Это причинно-следственная связь между переменными.
Важный момент: Другие имена зависимой и независимой переменной.
Зависимая переменная = Независимая переменная = Регрессия
Независимая переменная = Переменная-причина = Регрессор
Чтобы понять взаимосвязь зависимой и независимой переменных в регрессионном анализе: Поясним это на примере:
Q=ƒ(P,Ps,Yd)
Где Q есть объем спроса и зависимая переменная, на которую влияет независимая переменная P = цена, Ps = цена заменителей и Yd = доход
Это уравнение объясняет, что объем спроса является функцией всех этих переменных. Любое изменение этих переменных повлечет за собой изменение требуемого количества (остальные параметры остаются неизменными).
Причина использования слова «сохранение других вещей постоянными» заключается в том, что мы не сможем понять влияние одной независимой переменной на независимую переменную, если все переменные и их эффекты проверяются одновременно.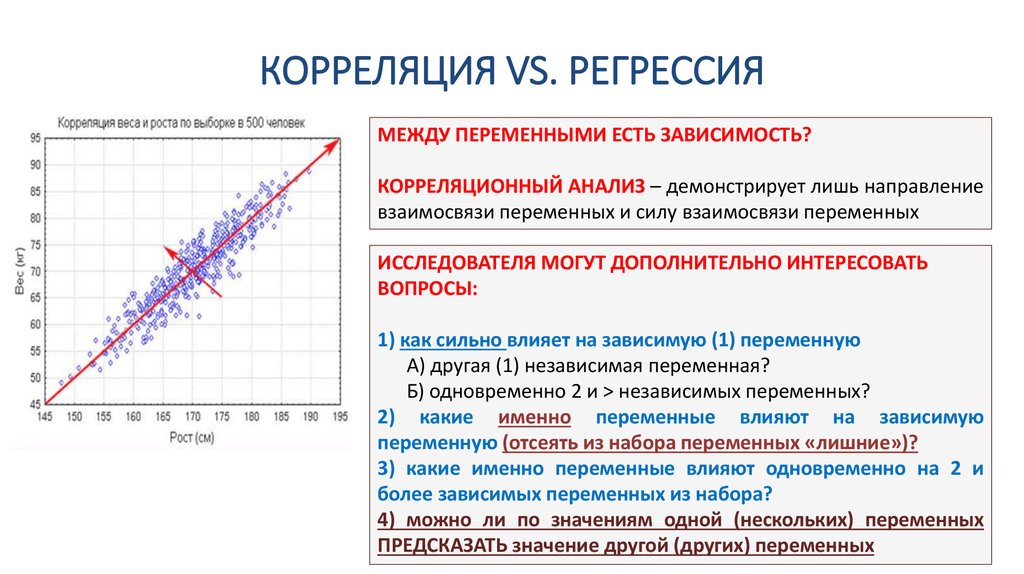 Вот почему мы оцениваем переменную таким образом, чтобы другие вещи оставались постоянными при анализе влияния одной переменной на зависимую переменную.
Вот почему мы оцениваем переменную таким образом, чтобы другие вещи оставались постоянными при анализе влияния одной переменной на зависимую переменную.
Обратите внимание, что большая часть эконометрического анализа связана с причинно-следственными связями. Тем не менее, вы должны помнить, что регрессионный анализ заключается не только в доказательстве связи между случаем и следствием. это скорее понимание силы и направления эффекта при условии, что переменная действительно имеет значимую связь или нет.
Простая регрессионная модель
Простая регрессионная модель представляет собой линейную модель с одним уравнением, которую можно объяснить следующим образом:
Y=β* + β¹X
Приведенные выше уравнения утверждают, что Y является зависимой переменной и представляет собой линейную функцию одного уравнения от независимой переменной X.
Почему мы называем это линейным?
Модель является линейной по следующим причинам:
- Если мы построим уравнения, это будет прямая линия.

- Это простое линейное уравнение с одной переменной, поскольку оно включает только один коэффициент переменной β1 . Это будет многомерная регрессионная модель, если она включает более одного коэффициента переменной.
- Это будет не кривая, а прямая линия, а прямая линия показывает постоянный наклон или скорость изменения в каждой точке.
- Коэффициент наклона показывает, что Y изменится, когда X увеличится на одну единицу.
Простой график линейной регрессии
Источник: Studenmund, Книга по эконометрике, глава 2, Простой регрессионный анализ .
Также обратите внимание, что в регрессионном анализе упор делается больше на коэффициенты наклона, такие как β1. В приведенной выше прямолинейной регрессии наклон постоянен на протяжении всей функции. а постоянный наклон означает, что изменение X на одну единицу приведет к такому же изменению Y.
Всякий раз, когда вы запускаете регрессию в любом программном обеспечении, суть всего уравнения заключается в том, что оно должно быть линейным.
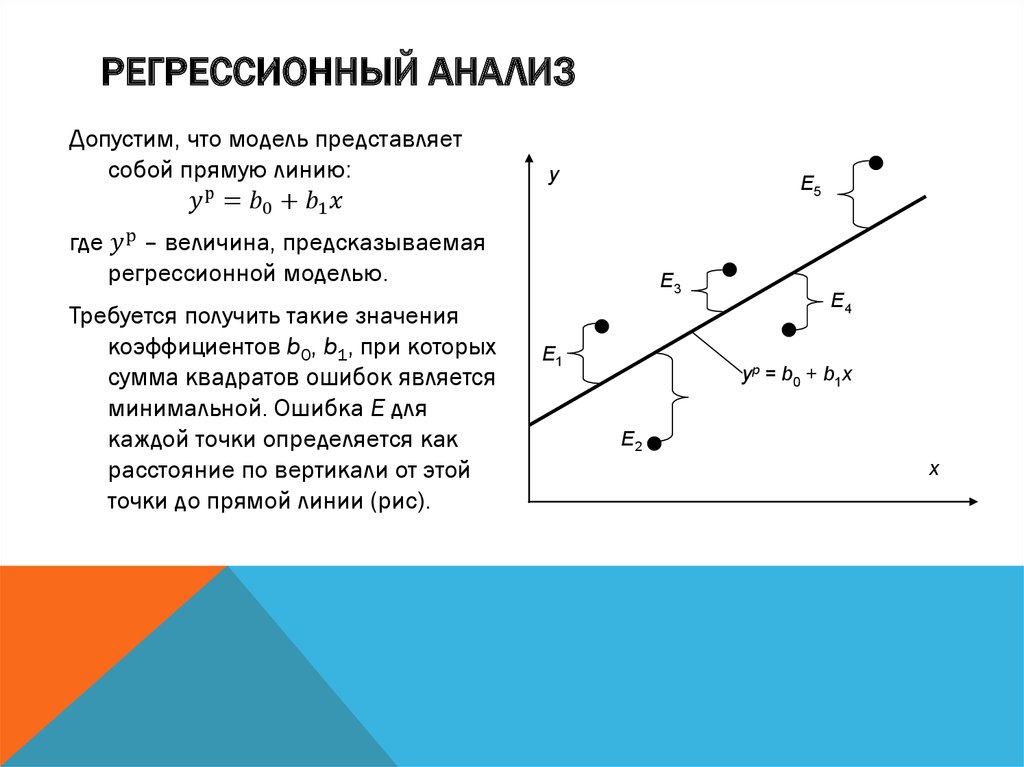 По полученным коэффициентам регрессии можно судить о том, как тот или иной фактор влияет на результат, сделать на этой основе дополнительные полезные выводы.
По полученным коэффициентам регрессии можно судить о том, как тот или иной фактор влияет на результат, сделать на этой основе дополнительные полезные выводы.