3DNews Offсянка Логистическая регрессия и дары машинного… Самое интересное в новостях Продолжаем закладывать основы, необходимые для понимания современных технологий ИИ. Вы узнаете больше базовых терминов, разберетесь в рабочих процессах, и уже близок тот день, когда вы сможете подобрать алгоритм под вашу задачу ⇣ Содержание Математическая истина, независимо от того, в Париже или в Тулузе, одна и та же. Блез Паскаль Логистическая регрессия – алгоритм с секретом. Нам понадобится небольшое предисловие о задачах машинного обучения в целом, чтобы понять, для какой цели применяется этот алгоритм. Это же регрессия, верно? Давайте разбираться. Какие задачи решает машинное обучение:
⇡#Что такое логистическая регрессия?Логистическая регрессия, как и линейная, была заимствована из статистики. Отличительной чертой логистической регрессии является то, что значением функции является вероятность. Вероятность чего? Закономерный вопрос. Давайте обо всем по порядку. На входе логистическая регрессия, как и линейная, принимает одну или несколько независимых переменных (признаков набора данных) и подсчитывает их взаимосвязь с зависимой переменной. Теперь наступает время ответить на вопросы, поставленные выше. Логистическая регрессия вычисляет вероятность того, что данное исходное значение принадлежит к определенному классу. Она используется для задач классификации: оценивает апостериорные вероятности принадлежности данного объекта к тому или иному классу. Для оценки модели логистическая регрессия применяет метод максимального правдоподобия. Он основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Попытаемся «на пальцах» сформулировать его принцип действия. Цель метода – оценить параметры распределения вероятностей. P(θ)=P(x=X|θ), где θ — значение параметра модели, P(θ) — вероятность появления значения θ, X — значение независимой переменной x, для которого определяется условная вероятность θ. Задача заключается в поиске таких значений параметров Θ = (θ1, θ2,…,θn), которые максимизируют функцию правдоподобия L(x|Θ). Для этого определяются оценки максимального правдоподобия (maximum likelihood estimates), для которых значения параметров являются наиболее «правдоподобными» по отношению к наблюдаемым данным. Если хочется еще больше математики, рекомендуем почитать про линейный дискриминант Фишера. ⇡#Линейная регрессия и логистическая регрессия: часто спрашивают на интервью сходство и различияОба этих алгоритма как альфа и бета машинного обучения и науки о данных. Сходство Обе модели являются контролируемыми алгоритмами машинного обучения и используют линейные уравнения для прогнозов. Вот и всё сходство. ⇡#Различия
⇡#Почему логистическая регрессия и какое нам до неё дело?Во-первых, это отличный способ старта в машинном обучении. Возьмите любой курс машобуча и посмотрите, с чего он начинается. Скорее всего, это будет линейная, а затем логистическая регрессия. Дело в том, что они воплощают два главных метода обучения с учителем – классификацию и регрессию. Таким образом, можно изучить всё необходимое без сложной и нагроможденной архитектуры. Если вы потратите на это время, досконально разберетесь в линейной и логистической регрессии и напишете код, вам по плечу будут и мощные новейшие алгоритмы ИИ. И да, машобуч — это подмножество искусственного интеллекта. Массачусетский институт технологий также придерживается этой позиции. Нейронные сети тоже вам покорятся, потому что каждый отдельный нейрон — своего рода логистическая регрессия. Искусственный нейрон имитирует работу живой нервной клетки, которая суммирует все входящие влияния, и если электрический потенциал суммы больше некоторого порога, то через принимающий нейрон будет распространяться потенциал действия («спайк»). Это же и есть бинарная классификация, где предсказываются 0 и 1, а в биологии этот принцип называется «все или ничего». Поэтому часто оказывается, что логистической регрессии вполне достаточно для решения проблемы. Благодаря удобству интерпретации результатов, а также своей способности выявлять наиболее весомые, значительные признаки набора данных, ЛР успешно применяется, например, в финансах и бизнесе для оценки платежеспособности заемщиков, сегментации пользователей (приобретет – не приобретет товар или услугу), классификации текстов (спам – не спам, токсичный комментарий – не токсичный и т. Этой информации должно быть достаточно, чтобы самостоятельно начать изучать логистическую регрессию. Рекомендуем использовать библиотеку scikit-learn и поэкспериментировать. Желаем успехов! Другие материалы цикла:
Источники:
⇣ Содержание
Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER. Материалы по теме Постоянный URL: https://3dnews.ru/1061487/logisticheskaya-regressiya-i-dari-mashinnogo-obucheniya Теги: машинное обучение, нейронная сеть, ии ⇣ Комментарии |
Что такое линейная регрессия?
Что такое линейная регрессия?Это модель машинного обучения, основанная на предположении, что зависимость в наблюдаемых данных можно описать простой прямой. Оказывается, такой моделью можно объяснить большое количество явлений. Помимо этого линейная регрессия хорошо изучена, имеет ряд полезных теоретических свойств, и ввиду своей простоты легко поддаётся интерпретации.
Оказывается, такой моделью можно объяснить большое количество явлений. Помимо этого линейная регрессия хорошо изучена, имеет ряд полезных теоретических свойств, и ввиду своей простоты легко поддаётся интерпретации.
Одна из главных задач машинного обучения – выявить закономерность между наблюдаемыми
переменными (их также называют регрессорами, признаками) и целевой. Например, по дозировке препарата и температуре пациента нужно спрогнозировать его давление (наблюдаемые переменные – дозировка и температура, целевая – давление), по дню месяца и влажности воздуха (наблюдаемые переменные) – температуру воздуха (целевая переменная).Задача восстановления зависимости между такими парами переменных называется регрессией (regressio — обратное движение, отход).
Зависимости между наблюдаемыми и целевой переменными могут быть любыми, в том числе сколь угодно сложными. Поэтому будем подбирать модель, которая по значениям наблюдаемых переменных будет выдавать значение целевой переменной, “близкое” к истинному, из ограниченного конкретного набора моделей Одним из наиболее простых классов (наборов) моделей является класс линейных моделей.
Линейная модель – модель, которая выражается линейной функцией. Слово “линейная” в названии объясняется тем, что графиком такой функции является прямая. В общем виде линейные функции одной переменной записываются так: h(x) = k*x + b, где k и b – произвольные числа. Пример линейной зависимости – зависимость расстояния от времени (s = v*t).
График линейной функции одной переменной
В случае, когда имеются несколько наблюдаемых переменных, линейные функции имеют вид: h(x_1, x_2, …, x_N) = a_0 + a_1*x_1 + a_2*x_2 + … + a_N*x_N, где a_0, a_1, …, a_N – также произвольные числа. График этой функции – тоже прямая, но уже в N-мерном пространстве.
График линейной функции двух переменныхТеперь соберём всё вместе:
Линейная регрессия – моделирование зависимости между наблюдаемыми и целевыми переменными с помощью линейных функций.
Есть модель, есть данные – пары, состоящие из наборов x-ов (наблюдаемых переменных) и соответствующих y (целевых переменных), последнее, что осталось – подобрать оптимальные коэффициенты, которые стоят перед переменными (например, числа k и b в случае одной наблюдаемой переменной). Оптимальность коэффициентов определяется функцией потерь, которая отображает, насколько прогнозы модели близки к целевым переменным. Их подбор называется обучением модели и производится специальными алгоритмами оптимизации (например, градиентным спуском). Эти коэффициенты называют весами модели, поскольку по значению коэффициента можно понять, насколько значима наблюдаемая переменная при нём (вспомним, что предсказание равно сумме произведений коэффициентов и соответствующих наблюдаемых переменных): чем больше коэффициент, тем больший вес имеет наблюдаемая переменная при нём, и наоборот, если коэффициент близок к 0, то переменная при нём практически никак не влияет на прогноз. Поэтому говорят, что линейная регрессия легко интерпретируема, то есть по модели легко можно, какие наблюдаемые переменные важны, а какие – нет.
После этапа обучения модель готова для использования – в полученную функцию (модель) нужно подставить интересующий набор x-ов и вычислить её значение, которое и будет являться прогнозом.
ПримерПредставьте, что вы предприниматель, который хочет прорекламировать свой продукт. В рамках рекламной кампании в разные месяцы вы тратите разные суммы денег и получаете соответственно разные показатели прироста выручки. В конце очередного месяца вы планируете бюджет на следующий и задаётесь вопросом: “Даст ли увеличение затрат на рекламу больший прирост выручки?” Зная ответ на этот вопрос, вы сможете более эффективно распределять ваши средства.
Наблюдаемой переменной в этом случае является бюджет на рекламу, то есть данные, которые известны, а целевой переменной – прирост выручки по окончании месяца, то есть данные, которые неизвестны и которые вы хотите спрогнозировать. Пусть x_1, x_2, …, x_10 – количество денег, которые были потрачены на рекламу в прошлых 10 месяцах, а y_1, y_2, …, y_10 – прирост выручки, зафиксированный в конце соответствующего месяца. Если предположить, что зависимость между x и y – линейная, то можно воспользоваться линейной регрессией.
Если предположить, что зависимость между x и y – линейная, то можно воспользоваться линейной регрессией.
Если предположение верно, то обучив линейную регрессию, можно довольно точно описать данные. Как можно видеть на графике выше, все красные точки (пары бюджет-прирост) расположены близко к синей прямой (модели). То, что точки не лежат на прямой, объясняется шумом в обучающих данных, который может быть вызван ошибками при измерениях или сборе данных.
ПрименимостьВзглянув на график выше, вы можете сделать вывод, что чем больше денег тратится на рекламу, тем больший прирост выручки вы получаете. Однако такое заключение довольно наивно и полагаться на него кажется сомнительной идеей. С большой долей вероятности, начиная с какого-то момента, увеличение трат не будет приводить к значимому приросту. Собрав ещё немного данных, вы заново строите график и получаете следующее:
Визуализация модели и дополненных данныхДействительно, модель сильно ошибается на новых данных – зелёные точки очень далеки от синей прямой. Более того, можно увидеть, что простой прямой недостаточно, чтобы объяснить все имеющиеся данные: невозможно провести прямую через красные и зелёные точки. В таких случаях говорят, что модель недостаточно выразительна. Данный пример иллюстрирует, что линейная регрессия не всегда применима. Однако существует множество явлений (и довольно сложных), которые ею можно описать. Например, линейная регрессия является фундаментальной моделью в экономике, её также часто применяют в медицине. Для сложных, нелинейных зависимостей используют в том числе и обобщённые линейные модели.
Более того, можно увидеть, что простой прямой недостаточно, чтобы объяснить все имеющиеся данные: невозможно провести прямую через красные и зелёные точки. В таких случаях говорят, что модель недостаточно выразительна. Данный пример иллюстрирует, что линейная регрессия не всегда применима. Однако существует множество явлений (и довольно сложных), которые ею можно описать. Например, линейная регрессия является фундаментальной моделью в экономике, её также часто применяют в медицине. Для сложных, нелинейных зависимостей используют в том числе и обобщённые линейные модели.
- Градиентный спуск
- Обобщённые линейные модели
Теги:глоссарий, линейная регрессия
Руководство для клинициста по интерпретации регрессионного анализа
Введение
Когда исследователи проводят клинические исследования для изучения факторов, связанных с заболеванием или его лечением, и состояний для улучшения ухода за пациентами и клинической практики, часто необходима статистическая оценка данных. Регрессионный анализ является важным статистическим методом, который обычно используется для определения взаимосвязи между несколькими факторами и исходами заболевания или для выявления соответствующих прогностических факторов для заболеваний [1].
Регрессионный анализ является важным статистическим методом, который обычно используется для определения взаимосвязи между несколькими факторами и исходами заболевания или для выявления соответствующих прогностических факторов для заболеваний [1].
Данная редакционная статья познакомит читателей с основными принципами и подходом к интерпретации результатов двух видов регрессионного анализа, широко используемых в офтальмологии: линейной и логистической регрессии.
Линейный регрессионный анализ
Линейная регрессия используется для количественной оценки линейной зависимости или ассоциации между непрерывной переменной ответа/результата или зависимой переменной по крайней мере с одной независимой или объясняющей переменной путем подгонки линейного уравнения к наблюдаемым данным [1]. Переменная, для которой решается уравнение, являющееся интересующим результатом или реакцией, называется зависимой переменной [1]. Переменная, которая используется для объяснения значения зависимой переменной, называется предикторной, объяснительной или независимой переменной [1].
В модели линейной регрессии зависимая переменная должна быть непрерывной (например, внутриглазное давление или острота зрения), тогда как независимая переменная может быть непрерывной (например, возраст), бинарной (например, пол), категориальной (например, возрастная макулярная стадия дегенерации или шкала тяжести диабетической ретинопатии), или их комбинация [1].
При исследовании влияния или ассоциации одной независимой переменной на непрерывную зависимую переменную этот тип анализа называется простой линейной регрессией [2]. Однако во многих случаях одной независимой переменной может быть недостаточно для адекватного объяснения зависимой переменной. Часто необходимо контролировать вмешивающиеся факторы, и в этих ситуациях можно выполнить многомерную линейную регрессию, чтобы изучить влияние или связь нескольких независимых переменных на зависимую переменную [1, 2]. При включении множества независимых переменных регрессионная модель оценивает влияние или вклад каждой независимой переменной, сохраняя при этом значения всех других независимых переменных постоянными [3].
При интерпретации результатов линейной регрессии есть несколько ключевых результатов для каждой независимой переменной, включенной в модель:
- 1.
Расчетный коэффициент регрессии — Расчетный коэффициент регрессии указывает направление и силу взаимосвязи или ассоциации между независимыми и зависимыми переменными [4]. В частности, коэффициент регрессии описывает изменение зависимой переменной для каждого изменения независимой переменной на одну единицу, если оно непрерывно [4]. Например, при изучении взаимосвязи между непрерывной прогностической переменной и внутриглазным давлением (зависимая переменная) коэффициент регрессии, равный 2, означает, что на каждую единицу увеличения предиктора приходится две единицы увеличения внутриглазного давления. давление. Если независимая переменная является бинарной или категориальной, то изменение на одну единицу представляет собой переход из одной категории в референтную [4].
 Например, при изучении взаимосвязи между бинарной переменной-предиктором, такой как пол, где «женский» установлен в качестве эталонной категории, и внутриглазным давлением (зависимая переменная), коэффициент регрессии, равный 2, означает, что в среднем мужчины у них внутриглазное давление на 2 мм рт. ст. выше, чем у женщин.
Например, при изучении взаимосвязи между бинарной переменной-предиктором, такой как пол, где «женский» установлен в качестве эталонной категории, и внутриглазным давлением (зависимая переменная), коэффициент регрессии, равный 2, означает, что в среднем мужчины у них внутриглазное давление на 2 мм рт. ст. выше, чем у женщин. - 2.
Доверительный интервал (ДИ) — ДИ, обычно устанавливаемый на уровне 95%, является мерой точности оценки коэффициента независимой переменной [4]. Большой ДИ указывает на низкий уровень точности, тогда как маленький ДИ указывает на более высокую точность [5].
- 3.
Значение P — значение p для коэффициента регрессии указывает, является ли взаимосвязь между независимыми и зависимыми переменными статистически значимой [6].

Логистический регрессионный анализ
Как и линейная регрессия, логистическая регрессия используется для оценки связи между одной или несколькими независимыми переменными и зависимой переменной [7]. Однако отличительной особенностью логистической регрессии является то, что зависимая переменная (результат) должна быть бинарной (или дихотомической), что означает, что переменная может принимать только два разных значения или уровня, например «1 против 0» или «да против нет». [2, 7]. Величина эффекта предикторов на зависимую переменную лучше всего объясняется с помощью отношения шансов (OR) [2]. ОШ используются для сравнения относительных шансов возникновения интересующего исхода с учетом воздействия интересующей переменной [5]. ОШ, равное 1, означает, что шансы события в одной группе такие же, как шансы события в другой группе; разницы нет [8]. ОШ > 1 означает, что одна группа имеет более высокие шансы возникновения события по сравнению с контрольной группой, тогда как ОШ < 1 означает, что одна группа имеет более низкие шансы возникновения события по сравнению с контрольной группой [8]. При интерпретации результатов логистической регрессии ключевые выходные данные включают ОШ, ДИ и p-значение для каждой независимой переменной, включенной в модель.
При интерпретации результатов логистической регрессии ключевые выходные данные включают ОШ, ДИ и p-значение для каждой независимой переменной, включенной в модель.
Клинический пример
Sen et al. исследовали связь между несколькими факторами (независимые переменные) и исходами остроты зрения (зависимая переменная) у пациентов, получающих антиваскулярную терапию эндотелиальным фактором роста по поводу макулярного отека (DMO) с помощью как линейной, так и логистической регрессии [9]. Многофакторная линейная регрессия продемонстрировала, что возраст (оценка –0,33, 95% ДИ – 0,48 до –0,19, p < 0,001) был значительно связан с остротой зрения с максимальной коррекцией (BCVA) через 100 недель при уровне значимости альфа = 0,05 [9].]. Коэффициент регрессии -0,33 означает, что МКОЗ в 100 недель снижается на 0,33 с каждым дополнительным годом старшего возраста.
Многопараметрическая логистическая регрессия также продемонстрировала, что возраст и состояние эллипсоидной зоны статистически значимо связаны с достижением буквенной оценки BCVA >70 букв через 100 недель при уровне значимости альфа = 0,05. Пациенты в возрасте ≥75 лет имели меньшие шансы достичь МКОЗ >70 букв в 100 недель по сравнению с пациентами моложе 50 лет, поскольку ОШ меньше 1 (ОШ 0,9).6, 95% ДИ от 0,94 до 0,98, p = 0,001) [9]. Точно так же у пациентов в возрасте от 50 до 74 лет также были меньшие шансы достичь МКОЗ >70 букв через 100 недель по сравнению с пациентами моложе 50 лет, поскольку ОШ меньше 1 (ОШ 0,15, 95). % ДИ от 0,04 до 0,48, p = 0,001) [9]. Кроме того, у пациентов с неинтактной эллипсоидной зоной были меньшие шансы достичь оценки букв BCVA >70 букв через 100 недель по сравнению с теми, у кого была интактная эллипсоидная зона (ОШ 0,20, 9).5% ДИ от 0,07 до 0,56; p = 0,002). С другой стороны, пациенты с неоцениваемой/сомнительной эллипсоидной зоной имели повышенные шансы достичь МКОЗ >70 букв через 100 недель по сравнению с пациентами с интактной эллипсоидной зоной, поскольку ОШ больше 1 (ОШ 2,26, 95% ДИ от 1,14 до 4,48; p = 0,02) [9].
Пациенты в возрасте ≥75 лет имели меньшие шансы достичь МКОЗ >70 букв в 100 недель по сравнению с пациентами моложе 50 лет, поскольку ОШ меньше 1 (ОШ 0,9).6, 95% ДИ от 0,94 до 0,98, p = 0,001) [9]. Точно так же у пациентов в возрасте от 50 до 74 лет также были меньшие шансы достичь МКОЗ >70 букв через 100 недель по сравнению с пациентами моложе 50 лет, поскольку ОШ меньше 1 (ОШ 0,15, 95). % ДИ от 0,04 до 0,48, p = 0,001) [9]. Кроме того, у пациентов с неинтактной эллипсоидной зоной были меньшие шансы достичь оценки букв BCVA >70 букв через 100 недель по сравнению с теми, у кого была интактная эллипсоидная зона (ОШ 0,20, 9).5% ДИ от 0,07 до 0,56; p = 0,002). С другой стороны, пациенты с неоцениваемой/сомнительной эллипсоидной зоной имели повышенные шансы достичь МКОЗ >70 букв через 100 недель по сравнению с пациентами с интактной эллипсоидной зоной, поскольку ОШ больше 1 (ОШ 2,26, 95% ДИ от 1,14 до 4,48; p = 0,02) [9].
Чем уже ДИ, тем точнее оценка; и чем меньше значение p (относительно альфа = 0,05), тем больше доказательств против нулевой гипотезы об отсутствии эффекта или связи.
Заключение
Проще говоря, линейная и логистическая регрессия являются полезными инструментами для оценки взаимосвязи между предикторными/объяснительными и исходными переменными для непрерывных и дихотомических исходов, соответственно, которые можно применять в клинической практике, например, для понимания риска факторы, связанные с интересующим заболеванием.
Ссылки
Шнайдер А., Хоммель Г., Блеттнер М. Линейная регрессия. Anal Dtsch Ärztebl Int. 2010; 107: 776–82.
Google Scholar
Бендер Р. Введение в использование моделей регрессии в эпидемиологии. В: Верма М, редактор. Эпидемиология рака. Методы молекулярной биологии. Хумана Пресс; 2009: 179–95.
Шобер П., Веттер ТР. Смешение в наблюдательных исследованиях. Анест Анальг. 2020;130:635.
Артикул Google Scholar
«>Шумилас М. Объяснение соотношения шансов. J Can Acad Детская подростковая психиатрия. 2010;19:227–9.
Артикул Google Scholar
Тизе М.С., Ронна Б., Отт Ю. П. Интерпретация ценностей и соображения. Дж. Торак Дис. 2016;8:E928–31.
Артикул Google Scholar
Шобер П., Веттер ТР. Логистическая регрессия в медицинских исследованиях. Анест Анальг. 2021; 132: 365–6.
Артикул Google Scholar
Zabor EC, Reddy CA, Tendulkar RD, Patil S. Логистическая регрессия в клинических исследованиях. Int J Radiat Oncol Biol Phys. 2022; 112: 271–7.

Артикул Google Scholar
Сен П., Гурудас С., Раму Дж., Патрао Н., Чандра С., Рашид Р. и др. Предикторы остроты зрения после лечения антиваскулярным эндотелиальным фактором роста при макулярном отеке, вторичном по отношению к окклюзии центральной вены сетчатки. Офтальмол Ретин. 2021;5:1115–24.
Артикул Google Scholar
Шобер П., Веттер ТР. Линейная регрессия в медицинских исследованиях. Анест Анальг. 2021; 132: 108–9.
Артикул Google Scholar
Скачать ссылки
R.E.T.I.N.A. исследовательская группа
Варун Чаудхари 1,2 , Мохит Бхандари 1,2 , Чарльз С. Вайкофф 5,6 , Собха Шивапрасад 8 , Лехана Табане 9012 5 2,7 , Питер Кайзер 9 , Дэвид Сарраф 10 , Софи Дж. Бакри 11 , Сунир Дж. Гарг 12 , Риши П. Сингх 13,14 , Фрэнк Г. Хольц 15 , Tien Y. Wong 16,17 и Robyn H. Guymer 3,4
Информация об авторе
Авторы и филиалы
Кафедра хирургии, Университет Макмастера, Гамильтон, Онтарио, Канада
Sofia Bzovsky, Mohit Bhandari & Varun Chaudhary
Департамент методов исследований здравоохранения, доказательства и воздействия, Университет МакМастера, Гамильтон, ON, Канада
Марк Р.
 Филлипс, Лехана Табейн, Мохит Бханхари и Варан Чаудари
Филлипс, Лехана Табейн, Мохит Бханхари и Варан ЧаудариЦентр глазных исследований Австралии, Королевская Викторианская офтальмологическая больница, Восточный Мельбурн, Виктория, Австралия Австралия
Робин Х. Гаймер
Retina Consultants of Texas (Retina Consultants of America), Хьюстон, Техас, США
Charles C. Wykoff
Глазной институт Blanton, Houston Methodist Hospital, H Оустон, Техас, США
Charles C. Wykoff
Отдел биостатистики, St. Joseph’s Healthcare Hamilton, Hamilton, ON, Canada
Lehana Thabane
NIHR Moorfields Biomedical Research Center, Moorfields Eye Больница, Лондон, Великобритания
Собха Шивапрасад
Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA
Peter Kaiser
Retinal Disorders and Ophthalmic Genetics, Stein Eye Institute, University of California, Los Angeles, CA, USA
Дэвид Сарраф
Отделение офтальмологии, клиника Майо, Рочестер, Миннесота, США США
Сунир Дж.
 Гарг
ГаргЦентр офтальмологической биоинформатики, Институт глаза Коула, Кливлендская клиника, Кливленд, Огайо, США
Риши П. Сингх
Кливлендская клиника Медицинский колледж Лернера, Кливленд, Огайо, США
Rishi P. Singh
Кафедра офтальмологии, Боннский университет, Бонн, Германия
Frank G. Holz
Сингапурский институт глазных исследований, Сингапур, Сингапур
Ti en Y. Wong
Сингапур Национальный глазной центр, Медицинская школа Duke-NUD, Сингапур, Сингапур
Tien Y. Wong
Авторы
- София Бзовски
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Академия
- Марк Р. Филлипс
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Робин Х. Гаймер
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Charles C.
 Wykoff
WykoffПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Lehana Thabane
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Mohit Bhandari
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Varun Chaudhary
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Consortia
от имени R.E.T.I.N.A. исследовательская группа
- Варун Чаудхари
- , Мохит Бхандари
- , Чарльз С. Викофф
- , Собха Шивапрасад
- , Лехана Табане
- , Питер Кайзер
- , Дэвид Сарраф
- , Софи Дж. Бакри
- , Сунир Дж. Гарг
- , Риши П. Сингх
- , Фрэнк Г. Хольц
- , Тьен Ю.
 Вонг
Вонг - и Робин Х. Гаймер
Вклады
SB отвечал за написание, критический обзор и обратную связь по рукописи. MRP отвечал за концепцию идеи, критический обзор и отзывы о рукописи. RHG отвечала за критический обзор и отзывы о рукописи. CCW отвечала за критический обзор и отзывы о рукописи. LT отвечал за критический обзор и отзывы о рукописи. МБ отвечал за концепцию идеи, критический обзор и отзывы о рукописи. ВК отвечал за концепцию идеи, критический обзор и отзывы о рукописи.
Автор, ответственный за переписку
Переписка с Варун Чаудхари.
Декларации этики
Конкурирующие интересы
SB: Нечего раскрывать. MRP: Нечего раскрывать. RHG: Консультативные советы: Bayer, Novartis, Apellis, Roche, Genentech Inc. — не имеют отношения к данному исследованию. CCW: Консультант: Acuela, Adverum Biotechnologies, Inc, Aerpio, Alimera Sciences, Allegro Ophthalmics, LLC, Allergan, Apellis Pharmaceuticals, Bayer AG, Chengdu Kanghong Pharmaceuticals Group Co, Ltd, Clearside Biomedical, DORC (Голландский центр офтальмологических исследований), EyePoint Pharmaceuticals , Gentech/Roche, GyroscopeTx, IVERIC bio, Kodiak Sciences Inc, Novartis AG, ONL Therapeutics, Oxurion NV, PolyPhotonix, Recens Medical, Regeron Pharmaceuticals, Inc, REGENXBIO Inc, Santen Pharmaceutical Co, Ltd и Takeda Pharmaceutical Company Limited; Научные фонды: Adverum Biotechnologies, Inc, Aerie Pharmaceuticals, Inc, Aerpio, Alimera Sciences, Allergan, Apellis Pharmaceuticals, Chengdu Kanghong Pharmaceutical Group Co, Ltd, Clearside Biomedical, Gemini Therapeutics, Genentech/Roche, Graybug Vision, Inc, GyroscopeTx, Ionis Pharmaceuticals , IVERIC bio, Kodiak Sciences Inc, Neurotech LLC, Novartis AG, Opthea, Outlook Therapeutics, Inc, Recens Medical, Regeneron Pharmaceuticals, Inc, REGENXBIO Inc, Samsung Pharm Co, Ltd, Santen Pharmaceutical Co, Ltd и Xbrane Biopharma AB — несвязанные этому исследованию. ЛТ: Нечего раскрывать. МБ: Исследовательские фонды: Пендофарм, Биовентус, Акумед — не имеют отношения к данному исследованию. Венчурный капитал: член Консультативного совета: Alcon, Roche, Bayer, Novartis; Гранты: Bayer, Novartis — не имеют отношения к данному исследованию.
ЛТ: Нечего раскрывать. МБ: Исследовательские фонды: Пендофарм, Биовентус, Акумед — не имеют отношения к данному исследованию. Венчурный капитал: член Консультативного совета: Alcon, Roche, Bayer, Novartis; Гранты: Bayer, Novartis — не имеют отношения к данному исследованию.
Дополнительная информация
Примечание издателя Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Перепечатка и разрешения
Об этой статье
Линейная регрессия в медицинских исследованиях
- Список журналов
- Липпинкотт Уильямс и Уилкинс, открытый доступ
- PMC7717471
Являясь библиотекой, NLM предоставляет доступ к научной литературе. Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Анестезия и обезболивание
Анест аналг. 2020 янв; 132 (1): 108–109.
Опубликовано в Интернете 14 декабря 2020 г. doi: 10.1213/ANE.0000000000005206
, MD, PhD, MMedStat * и , MD, MPH †
Информация об авторе Информация об авторских правах и лицензиях Отказ от ответственности
Связанная статья , см. стр. 110
КЛЮЧЕВОЙ МОМЕНТ:
Линейная регрессия используется для количественной оценки взаимосвязи между ≥1 независимыми (предикторными) переменными и непрерывной зависимой переменной (результатом).
В этом выпуске журнала Anesthesia & Analgesia Müller-Wirtz et al 1 сообщают о результатах исследования, в котором они использовали линейную регрессию для оценки взаимосвязи на модели крысы между концентрациями пропофола в тканях и концентрациями пропофола в выдыхаемом воздухе (рис.
Открыть в отдельном окне
Таблица 2, приведенная в Müller-Wirtz et al., 1 , показывающая расчетные взаимосвязи между концентрациями пропофола в тканях (или плазме) и концентрациями пропофола в выдыхаемом воздухе.5% доверительные интервалы как мера точности их оценок, а также коэффициент детерминации ( R 2 ). Представленные значения показывают, например, что (1) концентрация пропофола в выдыхаемом воздухе, по оценкам, увеличивается в среднем на 4,6 единицы, что равно коэффициенту наклона (регрессии), на каждую единицу увеличения концентрации пропофола в плазме; (2) можно ожидать, что «истинное» среднее увеличение будет лежать где-то между 3,6 и 5,7 единицами, на что указывает доверительный интервал коэффициента наклона; и (3) R 2 позволяет предположить, что около 71% вариабельности концентрации выдыхаемого вещества можно объяснить ее взаимосвязью с концентрацией пропофола в плазме.
Линейная регрессия используется для оценки связи ≥1 независимых (предикторных) переменных с непрерывной зависимой переменной (результат). 2 В самом простом случае, называемом «простой линейной регрессией», имеется только одна независимая переменная. Простая линейная регрессия соответствует прямой линии точкам данных, которые лучше всего характеризуют отношения
2 В самом простом случае, называемом «простой линейной регрессией», имеется только одна независимая переменная. Простая линейная регрессия соответствует прямой линии точкам данных, которые лучше всего характеризуют отношения
между зависимой ( Y ) переменной и независимой ( X ) переменной, с точкой пересечения оси y ( b 0 ), а коэффициентом регрессии является наклон ( b 904 04 1 ) этой строки:
Модель, включающая несколько независимых переменных, называется «множественная линейная регрессия» или «многопараметрическая линейная регрессия». Несмотря на то, что термин «линейная регрессия» предполагает обратное, его также можно использовать для моделирования криволинейных отношений.
Линейная регрессия — чрезвычайно универсальный метод, который можно использовать для решения различных исследовательских вопросов и целей исследования. Исследователи могут захотеть проверить наличие связи между категориальной (групповой) переменной (например, группой лечения или полом пациента) и количественным результатом (например, кровяным давлением). Двухвыборочный тест t и дисперсионный анализ 3 , которые обычно используются для этой цели, по существу являются частными случаями линейной регрессии. Однако линейная регрессия более гибкая, допуская > 1 независимую переменную и допуская непрерывные независимые переменные. Более того, когда имеется > 1 независимая переменная, исследователи также могут проверить взаимодействие переменных, другими словами, зависит ли эффект 1 независимой переменной от значения или уровня другой независимой переменной.
Двухвыборочный тест t и дисперсионный анализ 3 , которые обычно используются для этой цели, по существу являются частными случаями линейной регрессии. Однако линейная регрессия более гибкая, допуская > 1 независимую переменную и допуская непрерывные независимые переменные. Более того, когда имеется > 1 независимая переменная, исследователи также могут проверить взаимодействие переменных, другими словами, зависит ли эффект 1 независимой переменной от значения или уровня другой независимой переменной.
Линейная регрессия не только проверяет отношения, но также определяет их направление и силу. Коэффициент регрессии описывает среднее (ожидаемое) изменение зависимой переменной для каждого изменения независимой переменной на 1 единицу для непрерывных независимых переменных или ожидаемую разницу по сравнению с эталонной категорией для категориальных независимых переменных. Коэффициент детерминации, обычно называемый R 2 , описывает долю изменчивости переменной результата, которая может быть объяснена независимыми переменными. При простой линейной регрессии коэффициент детерминации также равен квадрату корреляции Пирсона между 9Значения 0403 x и y .
При простой линейной регрессии коэффициент детерминации также равен квадрату корреляции Пирсона между 9Значения 0403 x и y .
При включении нескольких независимых переменных регрессионная модель оценивает влияние каждой независимой переменной, сохраняя при этом значения всех других независимых переменных постоянными. 4 Таким образом, линейная регрессия полезна (1) для различения влияния различных переменных на исход и (2) для контроля других переменных, таких как систематическое смешение в обсервационных исследованиях или исходные дисбалансы из-за случайности в рандомизированном контролируемом исследовании. В конечном счете, линейную регрессию можно использовать для прогнозирования значения зависимой переменной результата на основе значения (значений) независимой переменной (переменных) предиктора.
Действительные выводы из линейной регрессии основаны на соблюдении ее допущений, включая
остатки — это различия между наблюдаемыми значениями и значениями, предсказанными регрессионной моделью, а остатки должны быть приблизительно нормально распределены и иметь примерно одинаковую дисперсия в диапазоне прогнозируемых значений;
остатки также считаются некоррелированными.
 Говоря простым языком, наблюдения должны быть независимы друг от друга; например, не должно быть повторных измерений у одних и тех же субъектов. Другие методы, такие как линейные модели смешанных эффектов, необходимы для коррелированных данных 5 ; и
Говоря простым языком, наблюдения должны быть независимы друг от друга; например, не должно быть повторных измерений у одних и тех же субъектов. Другие методы, такие как линейные модели смешанных эффектов, необходимы для коррелированных данных 5 ; имодель должна быть правильно указана, как более подробно описано в следующем абзаце.
В то время как Müller-Wirtz et al. 1 использовали простую линейную регрессию для решения своего исследовательского вопроса, исследователям часто приходится специфицировать модель с несколькими переменными и выбирать, какие независимые переменные включать и как моделировать функциональную взаимосвязь между переменными. (например, прямая линия по сравнению с кривой; включение условий взаимодействия).
Выбор переменных — тема для многих дискуссий, подробности которой выходят за рамки этой Статистической минуты. По сути, выбор переменных зависит от того, является ли целью модели понимание взаимосвязи между переменными или прогнозирование. Это также зависит от того, существует ли информированная априорная теория для выбора переменных и от того, должна ли модель контролировать переменные, которые не представляют основного интереса, но являются искажающими факторами, которые могут исказить взаимосвязь между другими переменными.
Это также зависит от того, существует ли информированная априорная теория для выбора переменных и от того, должна ли модель контролировать переменные, которые не представляют основного интереса, но являются искажающими факторами, которые могут исказить взаимосвязь между другими переменными.
Пропуск важных переменных или взаимодействий может привести к необъективным оценкам и модели, плохо описывающей истинные лежащие в основе отношения, тогда как включение слишком большого количества переменных приводит к моделированию шума (ошибки выборки) в данных и снижает точность оценок. Различные статистические данные и графики, в том числе скорректированные R 2 , Mallows C p и остаточные графики доступны для оценки качества соответствия выбранной модели линейной регрессии.
1. Мун Т.С., Ван де Путт П., Де Бердемакер Л., Шуман Р. Тучный пациент: факты, басни и лучшие практики. Анест Анальг. 2021; 132: 53–64. [PubMed] [Google Scholar]
2.
 На входе – признаки (features) объектов выборки, на выходе – вещественное число (стоимость товара, ожидаемая прибыль и т. д.).
На входе – признаки (features) объектов выборки, на выходе – вещественное число (стоимость товара, ожидаемая прибыль и т. д.).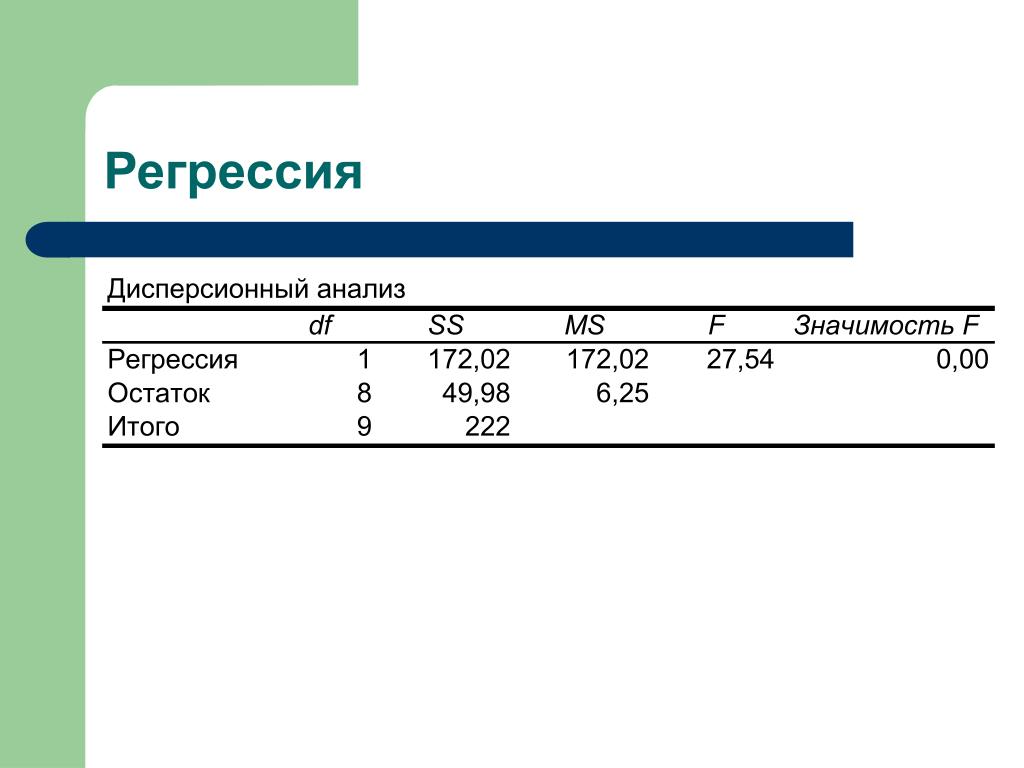 Также алгоритм обучения без учителя (потому что нет готовых ответов, на которых можно обучать модель).
Также алгоритм обучения без учителя (потому что нет готовых ответов, на которых можно обучать модель). Различие в том, что логистическая регрессия применяет сигмоидную функцию (также известна как логистическая, или логит-функция), которая позволяет предсказывать непрерывную переменную со значениями на отрезке [0, 1] при любых значениях независимых переменных. Фактически это распределение Бернулли (для тех, кому это интересно).
Различие в том, что логистическая регрессия применяет сигмоидную функцию (также известна как логистическая, или логит-функция), которая позволяет предсказывать непрерывную переменную со значениями на отрезке [0, 1] при любых значениях независимых переменных. Фактически это распределение Бернулли (для тех, кому это интересно). Способ – максимизировать функцию правдоподобия. Эта функция как раз определяет вероятность значений параметров регрессионной модели для заданного значения независимой переменной x=X:
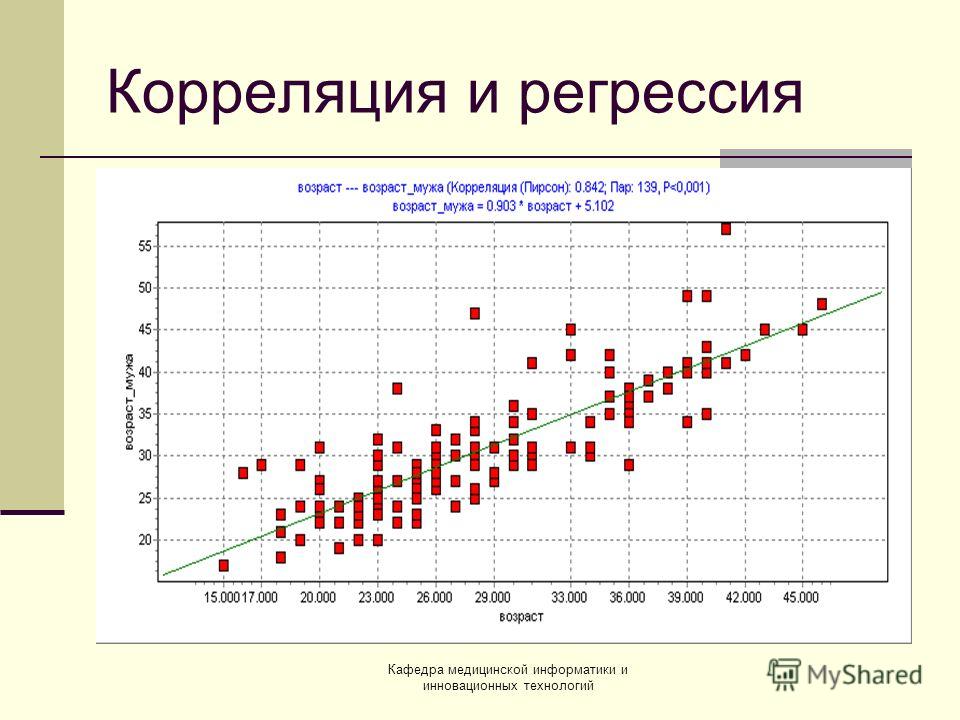
Способ – максимизировать функцию правдоподобия. Эта функция как раз определяет вероятность значений параметров регрессионной модели для заданного значения независимой переменной x=X: Посмотрим на их графики функций:
Посмотрим на их графики функций:
 Изучая эти два алгоритма, вы знакомитесь с основными понятиями, процессами и проблематикой машинного обучения, учитесь готовить данные к обработке, выбирать признаки, оценивать модель согласно различным метрикам (accuracy – доля правильных ответов, precision – точность, recall — полнота, F-measure – F-мера, ROC curve — кривая, Pearson correlation – корреляция Пирсона, mean squared error – корневая среднеквадратичная ошибка). Эти английские термины уже вошли в обиход, поэтому мы приводим их здесь. Отдельная статья о метриках машинного обучения планировалась в нашем цикле, пока не встретился вот этот отличный обзор.
Изучая эти два алгоритма, вы знакомитесь с основными понятиями, процессами и проблематикой машинного обучения, учитесь готовить данные к обработке, выбирать признаки, оценивать модель согласно различным метрикам (accuracy – доля правильных ответов, precision – точность, recall — полнота, F-measure – F-мера, ROC curve — кривая, Pearson correlation – корреляция Пирсона, mean squared error – корневая среднеквадратичная ошибка). Эти английские термины уже вошли в обиход, поэтому мы приводим их здесь. Отдельная статья о метриках машинного обучения планировалась в нашем цикле, пока не встретился вот этот отличный обзор.
 , Mirjalili V. Python machine learning: Machine learning and deep learning with Python, scikit-learn, and TensorFlow 2. – Packt Publishing Ltd, 2019. (Есть русский перевод этой книги).
, Mirjalili V. Python machine learning: Machine learning and deep learning with Python, scikit-learn, and TensorFlow 2. – Packt Publishing Ltd, 2019. (Есть русский перевод этой книги). Например, при изучении взаимосвязи между бинарной переменной-предиктором, такой как пол, где «женский» установлен в качестве эталонной категории, и внутриглазным давлением (зависимая переменная), коэффициент регрессии, равный 2, означает, что в среднем мужчины у них внутриглазное давление на 2 мм рт. ст. выше, чем у женщин.
Например, при изучении взаимосвязи между бинарной переменной-предиктором, такой как пол, где «женский» установлен в качестве эталонной категории, и внутриглазным давлением (зависимая переменная), коэффициент регрессии, равный 2, означает, что в среднем мужчины у них внутриглазное давление на 2 мм рт. ст. выше, чем у женщин.
 Филлипс, Лехана Табейн, Мохит Бханхари и Варан Чаудари
Филлипс, Лехана Табейн, Мохит Бханхари и Варан Чаудари Гарг
Гарг Wykoff
Wykoff Вонг
Вонг Говоря простым языком, наблюдения должны быть независимы друг от друга; например, не должно быть повторных измерений у одних и тех же субъектов. Другие методы, такие как линейные модели смешанных эффектов, необходимы для коррелированных данных 5 ; и
Говоря простым языком, наблюдения должны быть независимы друг от друга; например, не должно быть повторных измерений у одних и тех же субъектов. Другие методы, такие как линейные модели смешанных эффектов, необходимы для коррелированных данных 5 ; и