Релятивистская это: РЕЛЯТИВИСТСКИЙ | это… Что такое РЕЛЯТИВИСТСКИЙ?

Содержание

Релятивизм | Понятия и категории

РЕЛЯТИВИЗМ (лат. relativus — относительный) — признание относительности оценок и критериев оценки социальной реальности, идей, знаний, отсутствия абсолютных стандартов качества, критериев истинности.

Райзберг Б.А. Современный социоэкономический словарь. М., 2012, с. 438.

РЕЛЯТИВИЗМ (от лат. relativus — относительный) — принцип интерпретации мировоззренческих, культурных, познавательных систем, подчеркивающий моменты их исторической изменчивости, ситуативной обусловленности, замкнутости и несоизмеримости друг с другом. Релятивизм обычно связан с гисторицизмом и социологизмом, с представлениями о существовании охватывающих и несоизмеримых мировоззрений, концептуальных каркасов, структурирующих мышление людей различных эпох и культур.

Tags:

Философия

РЕЛЯТИВИЗМ (от лат. relativus — относительный), методология, принцип, состоящий в метафизической абсолютизации относительности и условности содержания познания.

Релятивизм проистекает из одностороннего подчёркивания постоянной изменчивости действительности и отрицания относительной устойчивости вещей и явлений. Гносеологические корни релятивизма — отказ от признания преемственности в развитии знания, преувеличение зависимости процесса познания от его условий (например, от биологических потребностей субъекта, его психического состояния или наличных логических форм и теоретических средств).

Tags:

Методология

РЕЛЯТИВИЗМ (от лат. relativus – относительный) – философский принцип, подчеркивающий примат связи объектов перед их субстанциальными свойствами, приоритет целостности, системности реальности перед ее отдельными частями, развития – перед сохранением. Формулировка принципа релятивизма, как недостоверности и относительности всякого знания, впервые встречается у древнегреческих софистов Протагора и Горгия, позднее – в античном скептицизме, а также в скептицизме Нового времени и в английском эмпиризме.

Tags:

Философия

РЕЛЯТИВИЗМ — философская точка зрения и методологический принцип, согласно которому все знания, все этические, эстетические и религиозные ценности рассматриваются как относительные, ограниченные во времени и пространстве и сравнимые с другими аналогичными, альтернативными ценностями. Относительность каких-либо достижений в различных областях культуры обуславливается преходящими конкретно-историческими условиями, в которых создавались ценности, а также психофизическим состоянием индивидов, их воспринимающих и использующих.

Tags:

Философия

РЕЛЯТИВИЗМ (лат. relativus — относительный) — признание относительности, условности, ограниченности человеческой деятельности в качестве основной ее характеристики. Понятие относительности, условности, обусловленности противопоставляется в Р. абсолютному, необусловленному. Р. выступает в различных формах. Он может быть «онтологическим»: мир изменчив, в нем нет ничего устойчивого, всё связано со всем, всё меняется относительно предыдущего этапа (софисты, античные скептики, отчасти современный прагматизм).

Tags:

Философия

РЕЛЯТИВИЗМ (RELATIVISME). Учение, утверждающее невозможность абсолютного учения. В широком смысле слова это, конечно, не более чем трюизм. Разве конечный разум способен получить абсолютный доступ к абсолюту, если абсолют есть бесконечный разум или вообще не есть разум? Подлинный смысл понятие релятивизма обретает только в специальном значении, выступающем в двух основных формах. Действительно, необходимо различать, с одной стороны, эпистемический, или

гносеологический, релятивизм и, с другой стороны, этический, или нормативный, релятивизм. Обе эти формы могут выступать как слитые воедино (например, у Монтеня), так и разделенные (например, у Спинозы — вторая форма, у Канта — первая)…

Tags:

Философия

РЕЛЯТИВИЗМ (лат. relativus — относительный) — философская концепция, утверждающая относительность, условность и субъективность человеческого познания. Признавая относительность знаний, релятивизм отрицает объективность познания, считает, что в наших знаниях не отражается объективный мир. Такая точка зрения ярко выражена уже в философии Горгия, хотя у него релятивизм имел положительное значение для развития диалектики. В целом же релятивизм характерен для агностических и субъективно-идеалистических систем. Он был, напр., одним из гносеологических источников физического идеализма.

Tags:

Методология

РЕЛЯТИВИЗМ (от лат. relativus — относительный) — теоретическая концепция и методологический принцип анализа и интерпретации онтологических построений, познания и культуры, полагающий абсолютной качественную нестабильность любых явлений, ставящий их в зависимость от различных обстоятельств и придающий им характер изменчивости, условности или случайности. В онтологии Р. отрицает понятие сущности, утверждая, что вещи существуют лишь в отношении к воспринимающему их субъекту (Беркли). В гносеологии Р.

Tags:

Методология

РЕЛЯТИВИСТСКИЙ — Что такое РЕЛЯТИВИСТСКИЙ?

Слово состоит из 14 букв: первая р, вторая е, третья л, четвёртая я, пятая т, шестая и, седьмая в, восьмая и, девятая с, десятая т, одиннадцатая с, двенадцатая к, тринадцатая и, последняя й,

Слово релятивистский английскими буквами(транслитом) — relyativistskii

Буква р встречается 1 раз. Слова с 1 буквой р
Буква е встречается 1 раз. Слова с 1 буквой е
Буква л встречается 1 раз. Слова с 1 буквой л
Буква я встречается 1 раз. Слова с 1 буквой я
Буква т встречается 2 раза. Слова с 2 буквами т
Буква и встречается 3 раза. Слова с 3 буквами и
Буква

в встречается 1 раз. Слова с 1 буквой в
Буква с встречается 2 раза. Слова с 2 буквами с
Буква к встречается 1 раз. Слова с 1 буквой к
Буква й встречается 1 раз. Слова с 1 буквой й

Релятивистская струя

Релятивистские струи, джеты (англ. jet) — струи плазмы, вырывающиеся из центров (ядер) таких астрономических объектов, как активные галактики, квазары и радиогалактики. Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
ru.wikipedia.org

РЕЛЯТИВИСТСКАЯ ПЛАЗМА

РЕЛЯТИВИСТСКАЯ ПЛАЗМА — плазма, в к-рой ср. энергия хаотич. движения частиц хотя бы одного сорта превышает энергию покоя этих частиц. Чаще всего релятивистской является электронная компонента плазмы.
Физическая энциклопедия.
— 1988

Релятивистские эффекты

РЕЛЯТИВИСТСКИЕ ЭФФЕКТЫ физ. явления, наблюдаемые при скоростях тел (ч-ц) v, сравнимых со скоростью света с. К ним относятся: релятив. сокращение продольных (в направлении движения тела) длин, релятив. замедление времени…
Физическая энциклопедия. — 1988

Релятивистские эффекты, явления, наблюдаемые при скоростях тел (частиц), сравнимых со скоростью света. К ним относятся: Лоренца — Фицджеральда сокращение, релятивистское замедление времени, увеличение массы тела с ростом его энергии и т. п.
БСЭ. — 1969—1978

РЕЛЯТИВИСТСКИЕ ЭФФЕКТЫ — физ. явления, наблюдаемые при скоростях тел (ч-ц) v, сравнимых со скоростью света с. К ним относятся: релятив. сокращение продольных (в направлении движения тела) длин, релятив.
замедление времени…
Физическая энциклопедия. — 1988

Релятивистская динамика

Основной закон динамики (второй закон Ньютона) для материальной точки имеет вид: В теории относительности импульс определяется по формуле. Величину. называют релятивистской массой, измеренной и ИСО…
www.edu.delfa.net

РЕЛЯТИВИСТСКАЯ ДИНАМИКА — раздел частной теории относительности, посвященный изучению движения материальных тел под действием приложенных к ним сил. В теории относительности свободные, т. е. не подверженные действию сил…
Математическая энциклопедия. — 1977-1985

Релятивистская механика

Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.
ru.wikipedia.org

Релятивистская механика, раздел теоретической физики, рассматривающий классические законы движения тел (частиц) при скоростях движения v, сравнимых со скоростью света.
БСЭ. — 1969—1978

Релятивистская механика (от лат. relativus — относительный механика) — механика Эйнштейна, основанная на принципе относительности и на постулате о постоянстве скорости света по всем направлениям относительно любой инерциальной системы отсчета.
Начала современного естествознания. — 2006

РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОНИКА

РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОНИКА — раздел высокочастотной электроники, посвящённый использованию релятивистских электронных пучков (РЭП) и (или) релятивистских эффектов для усиления, генерирования и преобразования эл. -магн. колебаний p волн.
Физическая энциклопедия. — 1988

Релятивистская астрофизика

Релятивистская астрофизика, раздел астрофизики, в котором изучаются астрономические явления и небесные тела в условиях, для которых неприменимы классическая механика и закон тяготения Ньютона.
БСЭ. — 1969—1978

РЕЛЯТИВИСТСКАЯ АСТРОФИЗИКА — раздел астрофизики, изучающий на основе общей теории относительности (теории тяготения А. Эйнштейна) свойства сверхплотных космических тел — нейтронных звезд и черных дыр.
Большой энциклопедический словарь

Релятивистская инвариантность

РЕЛЯТИВИСТСКАЯ ИНВАРИАНТНОСТЬ (лоренц-инвариантность) — независимость физ. законов и явлений от скорости движения наблюдателя (или, точнее, от выбора инерциальной системы отсчёта).
Физическая энциклопедия. — 1988

Релятивистская инвариантность, лоренцинвариантность, инвариантность (неизменность) законов природы относительно Лоренца преобразований, вытекающая из относительности теории.
БСЭ. — 1969—1978

РЕЛЯТИВИСТСКАЯ ИНВАРИАНТНОСТЬ — свойство физич. законов сохранять свой вид при преобразованиях Лоренца, описывающих переход от одной инер-циальной системы отсчета к другой.
Математическая энциклопедия. — 1977-1985

Релятивистская квантовая механика

РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА раздел теор. физики, в к-ром рассматриваются релятив. квант. законы движения микрочастиц (эл-нов и др.) в т. Физическая энциклопедия. — 1988

Релятивистская квантовая механика, раздел теоретической физики, в котором рассматриваются релятивистские (удовлетворяющие требованиям относительности теории) квантовые законы движения микрочастиц (электронов и др. ) в т. н. одночастичном приближении.
БСЭ. — 1969—1978

РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА — раздел теоретич. физики, в к-ром рассматриваются релятивистские квантовые законы движения микрочастиц (электронов и др.) в т. н. одночастичном приближении.
Физическая энциклопедия. — 1988

СТРУНА РЕЛЯТИВИСТСКАЯ

СТРУНА РЕЛЯТИВИСТСКАЯ — теоретич. одномерно-протяжённый релятивистский объект, функционал действия к-рого пропорционален площади мировой поверхности, заметаемой им при движении в пространстве-времени.
Физическая энциклопедия. — 1988

Русский язык

Релятиви́стский.
Орфографический словарь. — 2004

Релятив/и́ст/ск/ий.
Морфемно-орфографический словарь. — 2002

Слова из слова «релятивистский»
Слова на букву «р»
Слова, начинающиеся на «ре»
Слова c буквой «й» на конце
Слова c «ий» на конце
Слова, начинающиеся на «рел»
Слова, начинающиеся на «реля»
Слова, оканчивающиеся на «кий»
Слова, заканчивающиеся на «ский»

рель
релятивизм
релятивистический
релятивистский
релятивист
релятивность
релятивный

Релятивистская кинематика — материалы для подготовки к ЕГЭ по Физике

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Напомним, что основной задачей механики является описание движения, а именно — выяснение того, как меняются координаты тела с течением времени.

Для описания движения нужно иметь систему отсчёта. В классической механике, как мы знаем, в систему отсчёта входят три объекта: тело отсчёта (относительно которого рассматривается движение), жёстко связанная с телом отсчёта система координат, а также часы для измерения времени. Наблюдатель, находящийся в данной системе отсчёта, имеет возможность измерять координаты тела и сопоставлять эти координаты с показаниями часов. В результате наблюдатель получает зависимость координат тела от времени; располагая такой зависимостью, он может найти скорость тела и другие кинематические величины.

Одновременность событий

Сопоставление координат тела и показаний часов — ключевой момент. Здесь мы подходим к важнейшему понятию одновременности событий. Прежде всего, процитируем Эйнштейна.

Мы должны обратить внимание на то, что все наши суждения, в которых время играет какую-либо роль, всегда являются суждениями об одновременнных событиях. Если я, например, говорю: «Этот поезд прибывает сюда в 7 часов», — то это означает примерно следующее: «Указания маленькой стрелки моих часов на 7 часов и прибытие поезда суть одновременные события».

(А. Эйнштейн. «К электродинамике движущихся тел».)

Что такое одновременность в классической механике? Вопрос, казалось бы, ясен: события являются одновременными, если они происходят в один и тот же момент времени по часам наблюдателя. Отметим здесь два существенных момента.

• Неважно, происходят ли данные события в одной точке пространства или в различных точках. В классической механике мы спокойно говорим об одновременности пространственно разделённых событий.
• Понятие одновременности имеет абсолютный смысл: два события, одновременные в одной системе отсчёта, будут одновременными и в любой другой системе отсчёта. Во всех инерциальных системах отсчёта время течёт одинаково — это выражается равенством в преобразованиях Галилея.

Такое понимание одновременности, однако, носит интуитивный характер. И, что совсем плохо, оно базируется на предположении о мгновенности передачи взаимодействий. В самом деле, если сигналы от событий, происходящих в разных точках пространства, достигают наблюдателя мгновенно, то какая ему разница, насколько велико расстояние между этими событиями? Никакой задержки в приходе сигналов ведь не будет. Точно так же несущественно и то, покоится ли наблюдатель или движется — раз сигналы распространяются с бесконечной скоростью, события будут казаться наблюдателю одновременными независимо от факта его движения.

Но в действительности скорость сигнала является конечной и не может превышать скорость света в вакууме. Тем самым наше интуитивное понимание одновременности пространственно разделённых событий оказывается некорректным. Ведь если мы, держа в руках секундомер, фиксируем по нему время наступления окружающих событий и пытаемся судить об их одновременности, то нам придётся считаться с задержками прихода сигналов из различных точек пространства. Более того, эти задержки могут оказываться разными в зависимости от того, находимся ли мы в покоящейся системе отсчёта или в движущейся.

Что же получается — понятие одновременности вообще теряет смысл? Оказывается, нет! Эйнштейн предложил чёткую программу преодоления указанных трудностей. Суть её состоит в следующем: раз уж всё оказывается так плохо при измерении времени по одним-единственным часам наблюдателя, то давайте использовать много синхронно идущих часов, расставленных в разных точках пространства. Два события будут считаться одновременными, если совпадают показания часов, расположенных в тех точках, где произошли события.

А теперь — подробнее и по пунктам.

1. Пусть в некоторой точке пространства имеются часы. Если в этой точке происходит событие, то наши часы показывают время данного события. Таким образом, если в этой самой точке происходят два события, то мы всегда можем сказать, одновременны они или нет — просто сравнив показания наших часов в моменты наступления событий.

Итак, с определением одновременности событий, происходящих в одной точке пространства, проблем нет.

2. Для определения понятия одновременности пространственно разделённых событий нам понадобится много одинаковых часов, расставленных в пространстве достаточно часто. Каждые часы показывают время событий, происходящих в той точке, где эти часы расположены.

Чтобы была возможность судить об одновременности событий, происходящих в различных точках пространства, все эти часы должны идти синхронно, т. е. показывать одно и то же время. Но возникает естественный вопрос: а как этого добиться? Каким образом можно произвести синхронизацию часов?

3. Чтобы синхронизировать часы, расположенные в различных точках пространства, Эйнштейн предложил использовать световые сигналы.

Пусть в точках и имеются часы. Предположим, что из точки в точку посылается световой сигнал, который отражается в точке и возвращается назад в .

Пусть в момент отправления сигнала часы показывали , а в момент возвращения
сигнала показания тех же часов равны .

Правило Эйнштейна. По определению, часы и идут cинхронно, если в момент прихода сигнала в точку показания часов B равны .

Иными словами, часы должны показывать ровно середину промежутка между t1 и t2 .
Правило Эйнштейна иллюстрируется на рис. 1.

Рис. 1. Синхронизация часов по правилу Эйнштейна

Можно дать и другую, равносильную формулировку правила Эйнштейна.

Произведём в середине отрезка вспышку света. По определению, часы и идут синхронно, если в моменты прихода света в точки и показания часов совпадают.

4. Правило Эйнштейна основано на том, что скорость света в вакууме не зависит от направления распространения света. В самом деле, ведь при синхронизации часов мы считаем, что световой сигнал идёт с одной и той же скоростью в обоих направлениях: как от к , так и обратно от к .

Одинаковость скорости света по всем направлениям — это факт, подтверждаемый многочисленными опытами.

5. Может возникнуть следующий вопрос: а зачем вообще использовать какие-то световые сигналы? Давайте сначала поместим двое часов в точку , поставим их одинаково, а затем перенесём одни из этих часов в точку . Вот и получится пара синхронизированных часов в двух различных точках и !

Беда заключается в том, что такой способ не согласуется с правилом Эйнштейна. Если в точке уже имеются часы, синхронизированные по правилу Эйнштейна с часами , то перенесённые из часы покажут в точке время меньшее, чем первые. При этом перенесённые часы будут отставать тем больше, чем с большей скоростью они двигались! Об этом свидетельствует опыт, и мы скоро поймём, почему так получается.

Так что альтернативы правилу Эйнштейна нет: оно является простым, естественным и приводит к стройной теории, прекрасно согласующейся с экспериментом.

6. По правилу Эйнштейна мы можем синхронизировать любую пару часов. Но является ли это правило непротиворечивым? А именно, если мы синхронизировали указанным способом сначала часы и , а затем часы и , то окажутся ли при этом синхронизированными часы и ?

Хотелось бы думать, что да, однако из правила Эйнштейна это логически не следует (как, впрочем, не следует и ответ «нет»).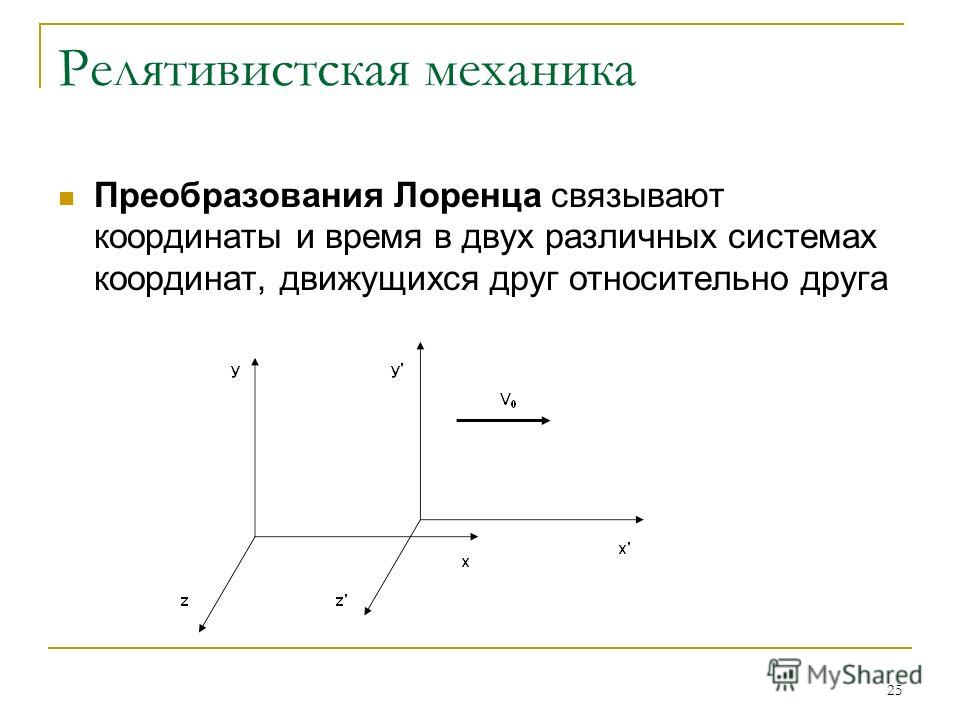 Эйнштейн постулировал непротиворечивость своего правила: да, часы и окажутся при этом синхронизированными. Данный постулат согласуется с экспериментом; принятие этого постулата не ведёт в дальнейшем к противоречиям в теории.

7. Итак, мы получили релятивистскую систему отсчёта с большим количеством часов. Все часы идут согласованно, они синхронизированы по правилу Эйнштейна. Время каждого события (местное время) измеряется по часам, расположенным в том месте, где событие совершилось.

Теперь можно дать определение одновременности событий.

Два пространственно разделённых события в данной системе отсчёта считаются одновременными, если при наступлении этих событий совпадают показания часов, расположенных в тех точках, где события произошли.

Можно запомнить более короткую формулировку: события одновременны, если их местные времена совпадают.

Как видим, существование максимальной скорости распространения сигналов ведёт к коренному пересмотру наших обыденных представлений о пространстве и времени. Оказалось, например, что понятие одновременности событий нуждается в строгом определении. Данное определение является непротиворечивым, согласуется с опытом и приводит к следствиям, весьма неожиданным с повседневной точки зрения.

Так, понятие одновременности, а также величины промежутков времени и расстояний между точками теряют свой абсолютный характер и становятся относительными, то есть зависящими от выбора той или иной системы отсчёта.

Относительность одновременности

Давайте ещё раз осмыслим определение одновременности событий. Мы смогли его дать, введя предварительно единое время для нашей системы отсчёта. Это единое время задаётся множеством синхронно идущих часов, расставленных в различных точках пространства.

Тем самым понятие одновременности пространственно разделённых событий оказывается «привязанным» к данной системе отсчёта. Выясняется, что два события, одновременные в одной системе отсчёта, могут оказаться не одновременными в другой системе отсчёта. В этом нетрудно убедиться на следующем простом примере.

Рассмотрим вагон, который движется вправо со скоростью (рис. 2). В точке , находящейся в центре вагона, происходит световая вспышка. Одновременно ли свет достигнет точек и , расположенных соответственно на задней и передней стенке вагона?

Рис. 2. Два события, одновременные в вагоне и не одновременные на земле

В системе отсчёта, связанной с вагоном, всё происходит точно так же, как в неподвижной лаборатории. По вагонным часам свет придёт в точки и одновременно.

Но в системе отсчёта, связанной с землёй, картина окажется иной. Точка движется навстречу сигналу, а точка удаляется от него; поэтому для достижения точки A свету потребуется пройти меньшее расстояние, чем для достижения точки . Но в земной системе отсчёта скорость света будет одинакова в обоих направлениях — ведь согласно второму постулату СТО скорость света не зависит от факта движения источника. Стало быть, по земным часам свет придёт в точку раньше, чем в точку .

Таким образом, два события — приход сигнала от источника в точки и — являются одновременными в системе отсчёта вагона и не одновременными в системе отсчёта земли.

В конце предыдущего листка было приведено противоречивое на первый взгляд рассуждение, в котором волновой фронт световой вспышки оказывался одновременно на двух различных сферах. Перечитайте это рассуждение ещё раз. Теперь становится ясно, что разрешение возникшего противоречия состоит в относительности понятия одновременности. Действительно, свет одновременно достигает поверхности сферы с центром в точке только в системе , но не в системе . И наоборот, свет одновременно достигает сферической поверхности с центром в точке только в системе , но не в системе .

Относительность промежутков времени

Снова рассмотрим вагон, который движется со скоростью . Предположим, что пассажир вагона подбрасывает яблоко; оно летит вертикально вверх, возвращается, и пассажир ловит его.

В системе отсчёта вагона события «яблоко брошено» и «яблоко поймано» происходят в одной точке. Промежуток времени между этими событиями, т. е. время полёта яблока в системе отсчёта вагона, измеряется по одним и тем же часам, расположенным в точке броска-ловли.

Но в системе отсчёта земли наши события происходят в различных пространственных точках. Момент броска яблока фиксируется по часам, расположенным в исходной точке, а момент ловли — по другим часам, расположенным в той точке, куда переместится вагон за время полёта яблока. Эти двое часов синхронизированы по правилу Эйнштейна. Время полёта яблока в системе отсчёта земли — это разность показаний вторых часов в момент ловли и первых часов в момент броска.

И вот оказывается, что время полёта яблока, измеренное по вагонным часам, будет меньше времени полёта, измеренного по часам на земле!

Разобраться в этом не сложно. Давайте только заменим яблоко на световой сигнал, который бегает между горизонтальными зеркалами, расположенными внутри вагона (рис. 3). Тем самым мы максимально упростим себе задачу.

Рис. 3. Промежуток времени относителен

Сначала рассмотрим ход сигнала в системе отсчёта вагона. Сигнал выходит из точки , идёт вертикально вверх, отражается от зеркала и возвращается назад в точку (рис. 3, слева).

Время распространения сигнала от нижнего зеркала к верхнему и обратно, измеренное по часам , обозначим . Если — расстояние между зеркалами, то выполнено соотношение

. 1

Теперь перейдём в систему отсчёта земли. Здесь сигнал будет двигаться между зеркалами по ломаной (рис. 3, справа).

Время распространения сигнала от нижнего зеркала к верхнему и обратно есть разность показаний синхронизированных часов: в точке в момент прихода сигнала и в точке в момент его отправления. Обозначим это время через .

За время сигнал проходит путь , равный , а вагон — путь . По теореме Пифагора имеем: или

Умножаем это равенство на 4:

С учётом ( 1) получим:

Отсюда можно выразить через :

. ( 2)

Полученная формула ( 2) носит совершенно общий характер. Пусть имеются две системы отсчёта и , причём система движется относительно K со скоростью . Рассмотрим два события, которые в системе происходят в одной точке пространства. Время между этими событиями в системе называется собственным временем. По часам системы между этими событиями проходит время , которое связано с собственным временем соотношением ( 2).

Обратите внимание, что в формуле ( 2) собственное время делится на величину, меньшую единицы; поэтому всегда выполнено неравенство . При этом время оказывается тем больше, чем с большей скоростью система движется относительно .

Данный эффект — так называемое релятивистское замедление времени — оказывается весьма существенным при скоростях, близких к скорости света. Давайте вернёмся к нашему примеру с пассажиром, подбрасывающим яблоко в вагоне. Предположим, что вагон движется со скоростью , а время полёта яблока по часам пассажира равно с. Тогда на земле между подбрасыванием яблока и его ловлей пройдёт время

Ну а теперь представьте, что с Земли отправляется звездолёт со скоростью . Космическое путешествие длится 10 лет по часам астронавтов. Вернувшись на Землю, астронавты обнаруживают, что попали в совершенно иную эпоху — ведь по земным часам прошло 224 года!

Звучит фантастично, но никакой фантастики тут нет — мы имеем дело со строгими фактами теории относительности. Ни с чем подобным нам сталкиваться не доводилось по той причине, что мы не умеем пока перемещаться с околосветовыми скоростями. Но как только эти скорости будут достигнуты, станет реальностью и машина времени для путешествий в будущее 🙂

Относительность расстояний

При выводе формулы ( 2) мы неявно предполагали, что расстояние между зеркалами одинаково как в вагоне, так и на земле. Но так ли это на самом деле? Да, это действительно так: вертикальные размеры предметов являются одними и те же как в вагонной, так и в земной системе отсчёта.

Чтобы убедиться в этом, давайте возьмём два одинаковых вертикальных стержня; один из них поместим в вагон, а другой оставим на земле. Оба стержня пусть будут на одной и той же высоте над землёй. Когда стержни поравняются друг с другом, концы одного стержня сделают засечки на другом стержне. Так вот, из принципа относительности следует, что эти засечки должны прийтись в точности на концы другого стержня.

В самом деле, пусть по засечкам оказывается, например, что вагонный стержень короче земного, т. е. движущийся стержень короче покоящегося. Но по принципу относительности инерциальные системы отсчёта полностью равноправны. Давайте перейдём в систему отсчёта вагона: там вагонный стержень будет покоиться, а земной — двигаться. Тогда получится, что движущийся стержень длиннее покоящегося. Противоречие!

Итак, поперечные размеры предметов одинаковы как в покоящейся, так и в движущейся системе отсчёта. Иначе обстоит дело с продольными размерами.

Вновь вернёмся к нашему вагону и рассмотрим стержень , расположенный вдоль вектора скорости вагона (рис. 4; изображать вагон надобности уже нет). Стержень, таким образом, двигается со скоростью v параллельно оси .

Рис. 4. Длина стержня относительна

Пусть — длина неподвижного стержня, измеренная в вагоне. Она называется собственной длиной стержня. Через обозначим длину движущегося стержня, измеренную на земле.

Для нахождения соотношения между и рассмотрим два события: 1) прохождение точки мимо фиксированной точки на оси ; 2) прохождение точки мимо точки .

В земной системе отсчёта наши события происходят в одной точке . Промежуток времени между этими событиями по земным часам пусть равен (это собственное время, разделяющее данные события). Очевидно, что

. ( 3)

В системе отсчёта вагона указанные события происходят в двух различных точках и . Промежуток времени между этими событиями по вагонным часам равен . Аналогично имеем:

. ( 4)

Приравнивая правые части формул ( 3) и ( 4), получим:

Но в силу формулы ( 2) имеем:

Отсюда получаем окончательную формулу:

. ( 5)

Как видим, собственная длина умножается на величину, меньшую единицы; стало быть, длина движущегося стержня будет меньше длины покоящегося стержня. Это так называемое лоренцево сокращение — все тела сокращают размеры в направлении своего движения.

Подчеркнём ещё раз: длина стержня в системе отсчёта, относительно которой стержень движется, меньше длины этого же стержня в системе отсчёта, относительно которой он покоится. Данный эффект связан лишь с особенностями измерительных процедур, свойственных теории относительности. Никаких реальных «сжатий» в движущемся стержне, разумеется, не происходит.

Преобразования Лоренца

Теперь мы можем вывести формулы, связывающие координаты и время фиксированного события в двух различных инерциальных системах отсчёта.

Пусть снова имеются две системы отсчёта: система и движущаяся относительно неё система (рис. 5). При начала и этих систем совпадают.

Рис. 5. К выводу преобразований Лоренца

Рассмотрим некоторое событие (например, вспышку света). В системе это событие происходит в точке с координатами в момент времени . В системе это же событие происходит в точке с координатами в момент времени .

Как мы уже выяснили, поперечные размеры тел в обеих системах отсчёта одни и те же.
Поэтому имеем: , .

Пусть — проекция точки на общую ось абсцисс.
Найдём длину отрезка в системах
и .

В системе отрезок покоится. Его длина равна — это собственная длина данного отрезка. В системе отрезок движется со скоростью , и его длина в силу формулы ( 5) равна . Но с другой стороны, в системе длина равна . Следовательно,

. ( 6)

Теперь аналогично найдём длину отрезка в системах и .

В системе отрезок покоится, его собственная длина равна . В системе отрезок движется со скоростью , и его длина равна . С другой стороны, длина в системе равна . Поэтому

. ( 7)

Из формулы ( 7) выразим . Полученное выражение подставим в ( 6) и выразим оттуда .
В результате получим:

, , , . ( 8)

Формулы ( 8) называются преобразованиями Лоренца. Они дают искомую связь координат и времени события в инерциальных системах отсчёта и . Эти релятивистские формулы, вытекающие из принципов СТО, служат заменой классическим преобразованиям Галилея, опирающимся на представления о мгновенности распространения взаимодействий.

При малых скоростях движения, т. е. при , мы можем считать отношение равным нулю. Тогда преобразования Лоренца переходят в соотношения:

, , , . ( 9)

Эти формулы есть не что иное, как преобразования Галилея. Мы видим, что преобразования Галилея служат предельным случаем преобразований Лоренца, когда скорости тел малы по сравнению со скоростью света. Поэтому при малых скоростях движения релятивистская механика Эйнштейна переходит в классическую механику Ньютона.

С системой равеств ( 6) и ( 7) можно поступить иначе. Выразим из ( 6), подставим в ( 7) и выразим оттуда . В результате придём к другому варианту записи преобразований Лоренца:

, , , . ( 10)

Формулы ( 8) задают переход из системы в систему . Формулы ( 10) задают обратный переход из системы в систему .

В предельном случае преобразования Лоренца ( 10) также переходят в преобразования Галилея:

, , , . ( 11)

Эти формулы, как легко видеть, полностью совпадают с формулами ( 9).

Релятивистский закон сложения скоростей

Опять рассмотрим наши системы отсчёта и . Пусть точка движется вдоль общего направления осей и (рис. 6).

Рис. 6. К выводу закона сложения скоростей

Пусть — скорость точки в системе ; в системе скорость этой точки пусть будет . Как связаны друг с другом и ?

Давайте вспомним, как выводится соответствующая формула в классической механике.
Берём первое из равенств ( 11) с заменой на :

Переходим к бесконечно малым приращениям координат и времени:

Делим обе части на :

Остаётся заметить, что , :

. ( 12)

Вот мы и получили классический закон сложения скоростей, которым неоднократно пользовались при решении задач механики.

Однако данный закон не может быть верным в теории относительности. В самом деле, рассмотрим вместо точки световой сигнал в вакууме, мчащийся в системе со скоростью . Согласно закону ( 12) получится, что скорость нашего сигнала в системе будет равна . Но это противоречит принципу относительности, в силу которого скорость света в вакууме имеет одно и то же значение во всех инерциальных системах отсчёта.

Возникновение данного противоречия не удивительно: ведь вывод формулы ( 12) базируется на преобразованиях Галилея, которые в теории относительности уступают место преобразованиям Лоренца. Поэтому правильный закон сложения скоростей нужно выводить теперь из преобразований Лоренца.

Идея вывода — та же самая, что и для формулы ( 12). Мы исходим из того, что

, . ( 13)

В соотношениях ( 12) переходим к бесконечно малым приращениям координат и времени:

, .

Делим первое из данных равенств на второе:

Разделим числитель и знаменатель правой части на :

Остаётся учесть соотношения ( 13) и написать:

. ( 14)

Это и есть релятивистский закон сложения скоростей, который приходит на смену классическому.

Теперь уже никакого противоречия не возникает: если скорость сигнала в системе ,
то в системе его скорость равна:

как того и требует принцип относительности.

При формулы ( 14), как нетрудно видеть, переходят в формулы ( 12).
Иными словами, при малых скоростях движения релятивистский закон сложения скоростей переходит в классический закон.

Релятивистский — понятие и значение

Рассмотрим что означает понятие и значение слова релятивистский (информация предоставлена intellect. icu).

Релятивистский это — 1. Соотносящийся по значение с существительное : релятивизм, релятивист, связанный с ними.
2. Характеризующийся релятивизмом.
3. Связанный с теорией относительности А. Эйнштейна.

Релятивистский это — 1. Релятивистская, релятивистское ( философия , научное ). Прилагательное к релятиви степень

(1)

При лицо к релятивизм, к релятиви степень

Релятивистские взгляды.

(2)

Спец.

Основанный на теории относительности.

Релятивистская механика. Релятивистская астрофизика.

Часть речи

Имя прилагательное (полное)

Словоформы

релятивистского, релятивистскому, релятивистским, релятивистском, релятивистская, релятивистской, релятивистскую, релятивистскою, релятивистское, релятивистские, релятивистских, релятивистскими

Синонимы wiki

релятивистический

Цифровое произношение

Релятивистский имеет soundex-Р431, metaphone-«рилaтивистский», double-metaphone RLTF.

См. также

6.5. Релятивистский закон сложения скоростей

… K:. Подставляя и t в формулу для vo Делим числитель и знаменатель на t Это равенство выражает собой релятивистский закон сложения скоростей При малых значениях скоростей и имеем т е релятивистский закон … (Физические основы механики)

6.6. Релятивистский импульс

… частицы , — сила действующая на частицу Сопоставим с классическим уравнением Мы приходим к выводу , что релятивистский импульс частицы равен Релятивистская масса Определив массу частицы m как коэффициент пропорциональности … … m как коэффициент пропорциональности между скоростью и. импульсом , получим , что масса частицы зависит от ее скорости Энергия в релятивистской динамике Для энергии частицы в теории относительности получается выражение :. Из следует … (Физические основы механики)

6. Элементы специальной теории относительности, преобразования Галилея и Лоренца, Постулаты Эйнштейна

… получения обратных преобразований достаточно поменять знак у скорости V. Величину общепринято называть релятивистским фактором (множителем ). С учетом этого обозначения преобразования Лоренца , оставляющие инвариантными уравнения … … есть только одна инвариантная скорость : это скорость . света в вакууме с Таким образом , имеем :. Релятивистское выражение для импульса должно при малых скоростях переходить в. нерелятивистское выражение , поэтому можно … (Физические основы механики)

4.7. Закон сохранения и превращения энергии, Теорема Кёнига

… факт , что частота генерируемого излучения . равна сумме частот двух исходных волн Релятивистская механика В релятивистской механике вводится понятие энергии-импульса (или просто четырехимпульса . ) Его введение … (Физические основы механики)

Частицы в магнитном поле

… Однако в ускорителях , где частицы разгоняются до скоростей , близких к. скорости света , приходится учитывать релятивистское выражение для импульса частицы Тогда уравнение движения будет иметь вид откуда … (Переменный электрический ток. Электромагнитное поле)

Время в физике, свойства и парадоксы, в физике, программировании, психологии

… аксиомами ,.задающими свойства времени как порядкового отношения Отсчет времени Как в классической , так и в релятивистской физике для отсчета . времени используется временная координата пространства-времени (в релятивистском случае — также и.пространственные … … использовать знак «+»; для будущего , а знак . «»; — для прошлого Однако смысл временной координаты в классическом и релятивистском случае различен . (см Ось времени ) Отсчет времени в астрономии и навигации Время в астрономии … (Введение в физику, основы)

релятивист

релятивное

Релятивистская механика

Все законы и теории классической механики справедливы для материальных тел, движущихся со скоростями, которые значительно меньше скорости света в самом вакууме.

Определение 1

Релятивистская механика – это обширный раздел физики, в который превращаются учения Ньютона в случае, если тело движется со скоростью, близкой к скорости света.

Рисунок 1. Релятивистский закон сложения скоростей. Автор24 — интернет-биржа студенческих работ

На таких сверхвысоких скоростях с элементами начинают происходить невероятные и совершенно неожиданные вещи такие как релятивистское спонтанное сокращение длины или замедление временного пространства. 2 } $ , где $∆t$ — проходящее между двумя событиями время, за которым следит некий неподвижный объект, $∆t_0$ — время, наблюдаемое между двумя движущимися предметами с точки зрения наблюдателя, находящегося в постоянном движении, $v$ — относительная скорость движения тела, $c$ — показатель света в вакууме.

Замечание 1

Из формулы видно, что $∆t_0 > ∆t$. То есть, время начинает двигаться медленнее для наблюдателя, который находятся в состоянии покоя.

Очень наглядно эффект замедления временного пространства можно наблюдать в космических полетах, где движение осуществляется с релятивистскими скоростями. Ведь время на борту такого летательного аппарата течёт медленнее, чем на планете. Так, если космический корабль будет двигаться со скоростью, равной примерно 0,95 скорости света, его полет будет длиться 13 земных лет, однако на самом деле по часам на самом шаттле пройдет всего 7,3 года. А если корабль будет в полёте 54 года по собственному времени, то на Земле за это время пробежит уже почти 5 млн. лет. Скорее всего, ход всех процессов, а не только часов, в полете будет замедленным. Это замедление называют в науке релятивистским сокращением длины движущегося физического тела.

Длина любого предмета в релятивистской механике напрямую зависит от скорости. Этот эффект характеризуется тем, что для наблюдателя, находящегося в состоянии покой, все движущиеся относительно него объекты имеют меньшую длину, чем в действительности. И чем выше скорость движения предмета, тем меньшим он кажется.

Постулаты релятивистской механики

В основе релятивистской механики лежат два основных постулата:

Принцип общей относительности движения физических тел, который предполагает равноправие всех инерциальных концепций отсчета. Любая система отсчета, которая движется относительно инерциальным принципам равномерно и прямолинейно начинает становиться инерциальной системой отсчета. Движение с постоянной по направлению и модулю скоростью называется прямолинейным движением. Таким образом, общность всех методов означает, что во всех законах физики эти системы будут одинаковы. Это утверждение называется в физике релятивистской инвариантностью.
Принцип стабильности скорости света в вакууме, который принято обозначать буквой $c$ ($c = 300000 км/с$). Эта закономерность означает, что световая скорость в пустоте не зависит от движения самого источника света. Форсирование физических процессов является максимальной вероятностью для дальнейшего распространения материальных взаимодействий.

Иными словами, первый постулат подразумевает, что, будучи в закрытой кабине и производя длительные наблюдения над электрическими и магнитными явлениями, невозможно сразу установить, покоится объект или осуществляет движение прямолинейно.

Замечание 2

Тем самым определяется относительность определений «стабильность» и «равномерное движение».

Используя эти два принципа, Эйнштейн смог создать новые математические преобразования Лоренца, наполнив их физическим смыслом. Таким образом, временной промежуток между двумя несвязанными между собой событиями непосредственно зависит от системы отсчета, то есть является относительным.

Основные положения релятивистской кинематики

Определение 2

Релятивистская кинематика — это универсальная теория относительности, которая основывается на двух постулатах: принцип инвариантности Эйнштейна и учения о постоянстве скорости света.

Данное направление в науке имеет собственные положения, которые заключаются в следующем:

относительность одновременности – два события, находящиеся в разных системах, являются одновременными, если они имеет место быть в один и тот же момент времени;
длина движущегося тела — в некоторой системе отсчета определяет расстояние между двумя основными точками координат, с которыми совпадают начало и конец тела в одно и то же временное пространство;
собственное время — интервал времени между определенными событиями, которые произошли в одной и той же точке собственной системы начального отсчета, тесно связанной с движущимся со скоростью объектом;
преобразование скоростей — устанавливает связь между проекциями скорости точки в двух произвольных зонах отсчета.

Можно утверждать, что интервал между двумя определенными событиями является инвариантом относительно преобразований Лоренца. В релятивистской механике кинетическую энергию элементарной частицы возможно представить, как разность полной энергии и энергии покоя.

На сегодняшний день релятивистская механика во многом стала инженерной наукой, с помощью которой экспертам удается анализировать и предотвращать возможное столкновение элементарных частиц, а также определять взаимодействие веществ и вообще всех физических процессов со скоростями, близкими к световой. Все современные и мощные ускорители заряженных элементов планируются и рассчитываются исключительно на основе релятивистской механики.

Урок 21. релятивистские эффекты — Физика — 11 класс

Физика, 11 класс

Урок №21. Релятивистские эффекты

На уроке рассматриваются понятия: энергия покоя, полная энергия частиц; связь массы и энергии в специальной теории относительности; релятивистский импульс частицы, релятивистская кинетическая энергия; принцип соответствия.

Глоссарий урока:

Релятивистская механика — раздел физики, где описывается движение частиц со скоростями близкими к скорости света.

Закон взаимосвязи энергии и массы — тело обладает энергией и при нулевой скорости, такую энергию называют энергией покоя.

Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии.

Безмассовыми называют частицы массы, которых в состоянии покоя равны нулю, они существуют только в движении, при этом во всех инерциальных системах отсчёта их импульс и энергия не равны нулю.

Массовыми называют частицы, для которых масса является важной характеристикой, мерой инертности тела.

Принцип соответствия – это подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматриваются как частный случай релятивистских законов при скоростях намного меньших скорость света.

Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай.

Обязательная литература:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 239 – 241.
Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 149

Дополнительная литература:

Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 253-260.
Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 311-315.
Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.144-157

Основное содержание темы

«Основы физики претерпели неожиданные и радикальные изменения благодаря смелости молодого и революционно мыслящего гения.»

Вернер Гейзенберг

Эти слова и множество других восхищённых эпитетов будут высказаны в адрес гениального учёного Альберта Эйнштейна. Эйнштейн не боялся опровергать общепринятые утверждения. Он разрушил представление об абсолютном времени и незыблемости пространства. Его теория утверждала, что есть движущиеся системы координат со своим относительным временем. А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости — опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.

Альберт (Einstein) Эйнштейн

14 марта 1879 г. – 18 апреля 1955 г.

Физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист.

По законам классической физики: масса – это мера инертности тела. Но Эйнштейн утверждает другое: масса – это мера энергии, содержащейся в теле.

Любое тело обладает энергией уже в силу своего существования. Альбертом Эйнштейном была установлена пропорциональность между энергией и массой:

На первый взгляд, простая формула, является фундаментальным законом природы, законом взаимосвязи энергии и массы.

Согласно этой формуле тело обладает энергией даже при нулевой скорости, в таком случае энергию называют E энергией покоя. А массу, которая входит в формулу Эйнштейна назовём m₀массой покоя.

Как же будет выглядеть закон взаимосвязи массы и энергии для движущегося тела? К нему добавляем радикал (релятивистский множитель) из преобразований Лоренца:

Такую формулу называют релятивистской энергией или полной энергией движущегося тела.

Релятивистская механика — раздел физики, где описываются движения тел и частиц со скоростями близкими к скорости света, где используются преобразования Лоренца, перехода из одной инерциальной системы в другую, когда одна система движется относительно другой со скоростью вдоль оси ОХ.

Любые изменения физических величин, связанные с сокращением размеров:

эффект замедления времени:

изменение массы тела при изменении энергии:

закон сложения скоростей:

в специальной теории относительности называют релятивистскими изменениями.

По законам классической физики полная энергия равна сумме кинетической и потенциальной энергий тела или частицы

Отсюда выразим кинетическую энергию тела

Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии

В классической физике кинетическая энергия вычисляется по формуле

Получим ещё одно выражение

Выразим кинетическую энергию из формулы релятивистской энергии:

Поставим релятивистский радикал, который можно преобразовать при малых скоростях и получим релятивистскую кинетическую энергию частицы:

Или другой способ выражения кинетической энергии, если использовать классическую кинетическую энергию, то получим

— выражение для определения релятивистской кинетической энергии.

Путём не сложных математических вычислений можно доказать, что формула определения кинетической энергии в классической физикеи формула кинетической энергии в релятивистской физике равны между собой.

Давайте проверим работают ли главные законы механики — законы Ньютона в релятивистской физике.

Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.

Первый постулат СТО Эйнштейна: все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.

Внимание! Они не противоречат друг другу!

Третий закон Ньютона: силы с которыми тела действуют друг на друга равны по модулю и направлены вдоль одной прямой в противоположные стороны. Этот закон тоже работает в релятивистской физике (смотрите первый постулат СТО).

А что же со вторым законом классической механики? Второй закон Ньютона: ускорение тела прямо пропорционально силе и обратно пропорционально его массе.

Рассмотрим предельный случай: если на тело долгое время t (время стремится к бесконечности) действовать с постоянной силой F = const, то ускорение будет постоянным a = const. Ускорение в свою очередь, зависит от скорости, с которой движется тело:

Отсюда скорость тоже будет стремиться к бесконечности, а это невозможно (смотрите второй постулат СТО), так как скорость тела или частицы не может быть больше предельного значения скорости света ()!

Но давайте рассмотрим другую формулировку второго закона Ньютона, когда сила прямо пропорциональна изменению импульсов тела ко времени этого изменения:

В классической механике импульс равен произведению массы тела или частицы на его скорость: , где m – постоянная величина, мера инертности тела.

В релятивистской механике выражение импульса можно записать, используя преобразования Лоренца:

При скоростях намного меньших, чем скорость света 𝟅с, формула принимает вид классической механики Ньютона

Эти проявления — подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматривают как частный случай релятивистских законов при скоростях намного меньших скорости света и называют принципом соответствия. Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.

В природе существуют такие частицы (фотоны, мюоны, нейтрино), скорость которых равна или близка к скорости света. Массы таких частиц в состоянии покоя равны нулю, эти частицы называют безмассовыми. Они существуют только в движении, но во всех инерциальных системах отсчёта их импульс и энергия не равны нулю. Тогда подтверждается утверждение Эйнштейна, что масса – это мера энергии тела. Частицы, для которых масса является важной характеристикой — мерой инертности, называют массовыми.

Найдём соотношение между энергией и импульсом:

Взаимно уничтожаются подкоренные выражения, сокращается произведение массы на скорость света, и мы получим простое соотношение энергии и импульса, где нет зависимости от массы.

Энергия и импульс связаны соотношением

Поэтому во всех инерциальных системах отсчёта импульс и энергия не равны нулю. При превращениях элементарных частиц, обладающих массой покоя , в частицы у которых , их энергия покоя целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя.

Во всех инерциальных системах отсчёта импульс частицы и её энергия связаны соотношением:

или

— эта формула является фундаментальным соотношением энергии и импульса для массовых частиц релятивистской механики. Эти соотношения экспериментально подтверждены.

Следовательно, для безмассовых частиц, где или , выражение примет вид

Основное выражение энергии через её импульс записывают так:

Отсюда, масса, движущейся частицы, будет равна

Если частица покоится, то её значение можно определить из основной формулы Эйнштейна взаимосвязи массы и энергии:

В обычных условиях, при нагревании тела или его охлаждении, при химической реакции, эти приращения массы происходят, их можно вычислить, но изменения массы не так заметны. Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.

Рассмотрим задачи тренировочного блока урока:

1. Чтобы выработать количество энергии, которой обладает тело массой 1 кг, Красноярской ГЭС потребуется времени _________ суток (1,5·10⁷; 173,6; 182,3). Мощность Красноярской ГЭС 6000МВт.

Дано:

m = 1 кг

P = 6000 МВт = 6·10⁹Вт

t — ? (сутки)

Воспользуемся выражением, описывающим зависимость энергии тела от массы:

И зависимостью мощности от работы и времени:

Выразим секунды в часах, а затем в сутках:

Ответ: 173,6 суток.

2. Чему равен импульс протона, летящего со скоростью 8,3·10⁷ м/с? На сколько будет допущена ошибка, если пользоваться формулами классической физики? Данные поученных вычислений занесите в таблицу:

Физические величины	Показатели
Масса покоя протона, m	1,67·10^-27кг
Скорость света, с	3·10⁸ м/с
Скорость движения протона, 𝟅	8,3·10⁷ м/с
Импульс протона по классическим законам, р_к	?
Импульс протона по релятивистским законам, р_р	?
Разница в вычислениях импульса протона,	?

Воспользуемся формулами для определения импульса релятивистским и классическим способами:

Вычислим разницу показаний:

Физические величины	Показатели
Масса покоя протона, m	1,67·10^-27кг
Скорость света, с	3·10⁸ м/с
Скорость движения протона, 𝟅	8,3·10⁷ м/с
Импульс протона по классическим законам, р_к	1,38·10^-19кг·м/с
Импульс протона по релятивистским законам, р_р	5,2·10^-19 кг·м/с
Разница в вычислениях импульса протона,	в 3,8 раза

относительность | Определение, уравнения и факты

инвариантность скорости света

Смотреть все СМИ

Ключевые люди:: Альберт Эйнштейн Анри Пуанкаре Бернхард Риманн Артур Эддингтон Герман Вейль

Похожие темы:: замедление времени парадокс близнецов специальная теория относительности общая теория относительности гипертайм

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

относительность , обширные физические теории, созданные физиком немецкого происхождения Альбертом Эйнштейном. Своими теориями специальной теории относительности (1905 г.) и общей теории относительности (1915 г.) Эйнштейн опроверг многие предположения, лежащие в основе более ранних физических теорий, переопределив в процессе фундаментальные концепции пространства, времени, материи, энергии и гравитации. Наряду с квантовой механикой теория относительности занимает центральное место в современной физике. В частности, теория относительности обеспечивает основу для понимания космических процессов и геометрии самой Вселенной.

E = mc ²

Посмотреть все видео к этой статье друг друга так, что наблюдатель не может с помощью чисто механических экспериментов отличить одно от другого. Начав с поведения света (и всех других электромагнитных излучений), специальная теория относительности делает выводы, противоречащие повседневному опыту, но полностью подтверждаемые экспериментами. Специальная теория относительности показала, что скорость света — это предел, к которому может приблизиться, но не достичь любой материальный объект; это происхождение самого известного уравнения в науке, E = м c ² ; и это привело к другим мучительным последствиям, таким как «парадокс близнецов».

«Общая теория относительности» занимается гравитацией, одной из фундаментальных сил Вселенной. (Другими являются электромагнетизм, сильное взаимодействие и слабое взаимодействие.) Гравитация определяет макроскопическое поведение, поэтому общая теория относительности описывает крупномасштабные физические явления, такие как динамика планет, рождение и смерть звезд, черных дыр и эволюция Вселенная.

Специальная и общая теория относительности оказали глубокое влияние на физическую науку и на существование человека, особенно в области применения ядерной энергии и ядерного оружия. Кроме того, относительность и ее переосмысление фундаментальных категорий пространства и времени послужили основой для определенных философских, социальных и художественных интерпретаций, которые по-разному повлияли на человеческую культуру.

Тест «Британника»

Физика и законы природы

Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.

Космология до теории относительности

Механическая вселенная

Теория относительности изменила научную концепцию Вселенной, которая началась с попыток понять динамическое поведение материи. В эпоху Возрождения великий итальянский физик Галилео Галилей вышел за рамки философии Аристотеля и представил современное изучение механики, которое требует количественных измерений тел, движущихся в пространстве и времени. Его работа и работы других привели к основным понятиям, таким как скорость, которая представляет собой расстояние, которое тело проходит в заданном направлении в единицу времени; ускорение, скорость изменения скорости; масса, количество вещества в теле; и сила, толчок или тяга к телу.

Следующий важный шаг произошел в конце 17 века, когда гениальный британский ученый Исаак Ньютон сформулировал свои три знаменитых закона движения, первый и второй из которых представляют особый интерес в теории относительности. Первый закон Ньютона, известный как закон инерции, гласит, что тело, на которое не действуют внешние силы, не испытывает никакого ускорения — либо остается в покое, либо продолжает двигаться прямолинейно с постоянной скоростью. Второй закон Ньютона гласит, что сила, приложенная к телу, изменяет его скорость, вызывая ускорение, пропорциональное силе и обратно пропорциональное массе тела. При построении своей системы Ньютон также определил пространство и время, приняв и то, и другое за абсолюты, не подверженные влиянию чего-либо внешнего. Время, писал он, «течет равномерно», а пространство «всегда остается одинаковым и неподвижным».

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Законы Ньютона доказали свою применимость во всех приложениях, например, при расчете поведения падающих тел, но они также послужили основой для его выдающегося закона всемирного тяготения (термин, происходящий от латинского gravis , или «тяжелый», использовался по крайней мере с 16 века). Начав с наблюдения (возможно, мифического) падающего яблока, а затем рассматривая Луну, вращающуюся вокруг Земли, Ньютон пришел к выводу, что между Солнцем и его планетами действует невидимая сила. Он сформулировал сравнительно простое математическое выражение для силы тяготения; в нем говорится, что каждый объект во Вселенной притягивает любой другой объект с силой, действующей через пустое пространство и зависящей от массы объектов и расстояния между ними.

Закон всемирного тяготения блестяще объяснил механизм кеплеровских законов движения планет, которые немецкий астроном Иоганн Кеплер сформулировал в начале XVII века. Механика Ньютона и закон всемирного тяготения вместе с его предположениями о природе пространства и времени казались полностью успешными в объяснении динамики Вселенной, от движения на Земле до космических событий.

Однако этот успех в объяснении явлений природы подвергся проверке с неожиданной стороны — поведения света, чья неосязаемая природа веками озадачивала философов и ученых. В 1865 году шотландский физик Джеймс Клерк Максвелл показал, что свет представляет собой электромагнитную волну с колеблющимися электрическими и магнитными компонентами. Уравнения Максвелла предсказывали, что электромагнитные волны будут распространяться в пустом пространстве со скоростью почти точно 3 × 10 ⁸ метра в секунду (186 000 миль в секунду) — т. е. согласно измеренной скорости света. Эксперименты вскоре подтвердили электромагнитную природу света и установили его скорость как фундаментальный параметр Вселенной.

Замечательный результат Максвелла ответил на давние вопросы о свете, но поднял еще один фундаментальный вопрос: если свет — это движущаяся волна, какая среда поддерживает ее? Океанские волны и звуковые волны состоят из поступательного колебательного движения молекул воды и атмосферных газов соответственно. Но что вибрирует, создавая движущуюся световую волну? Или, другими словами, как энергия, воплощенная в свете, перемещается из точки в точку?

Для Максвелла и других ученых того времени ответ заключался в том, что свет распространяется в гипотетической среде, называемой эфиром (aether). Предположительно, эта среда пронизывала все пространство, не препятствуя движению планет и звезд; однако он должен был быть более жестким, чем сталь, чтобы световые волны могли проходить через него с высокой скоростью, подобно тому, как натянутая гитарная струна поддерживает быстрые механические вибрации. Несмотря на это противоречие, идея эфира казалась существенной, пока окончательный эксперимент не опроверг ее.

В 1887 году американский физик немецкого происхождения А.А. Майкельсон и американский химик Эдвард Морли провели исключительно точные измерения, чтобы определить, как движение Земли в эфире влияет на измеренную скорость света. В классической механике движение Земли прибавляло бы или вычитало из измеренной скорости световых волн точно так же, как скорость корабля прибавляла бы или вычитала из скорости океанских волн, измеренной от корабля. Но эксперимент Майкельсона-Морли дал неожиданный результат, поскольку измеренная скорость света оставалась неизменной независимо от движения Земли. Это могло означать только то, что эфир не имел смысла и что поведение света не могло быть объяснено классической физикой. Вместо этого объяснение возникло из специальной теории относительности Эйнштейна.

Релятивистская энергия | Физика

Цели обучения

К концу этого раздела вы сможете:

Вычислять полную энергию релятивистского объекта.
Вычислите кинетическую энергию релятивистского объекта.
Опишите энергию покоя и объясните, как ее можно преобразовать в другие формы.
Объясните, почему массивные частицы не могут достичь C.

Рис. 1. В Национальном эксперименте со сферическими торами (NSTX) есть термоядерный реактор, в котором происходит синтез изотопов водорода с образованием гелия. В этом процессе относительно небольшая масса топлива преобразуется в большое количество энергии. (кредит: Принстонская лаборатория физики плазмы)

Токамак — это форма экспериментального термоядерного реактора, который может преобразовывать массу в энергию. Для этого требуется понимание релятивистской энергии. Ядерные реакторы являются доказательством сохранения релятивистской энергии.

Закон сохранения энергии — один из важнейших законов физики. Мало того, что энергия имеет много важных форм, каждая форма может быть преобразована в любую другую. Мы знаем, что в классическом понимании общее количество энергии в системе остается постоянным. Релятивистски энергия по-прежнему сохраняется при условии, что ее определение изменено, чтобы включить возможность превращения массы в энергию, как в реакциях, происходящих в ядерном реакторе. Релятивистская энергия намеренно определена таким образом, чтобы она сохранялась во всех инерциальных системах отсчета, как и в случае с релятивистским импульсом. Как следствие, мы узнаем, что несколько фундаментальных величин связаны способами, неизвестными в классической физике. Все эти соотношения проверяются экспериментом и имеют фундаментальные последствия. Измененное определение энергии содержит некоторые из наиболее фундаментальных и захватывающих новых открытий в природе, обнаруженных в новейшей истории.

Полная энергия и энергия покоя

Первый постулат относительности гласит, что законы физики одинаковы во всех инерциальных системах отсчета. Эйнштейн показал, что закон сохранения энергии верен релятивистски, если мы определяем энергию как включающую релятивистский фактор.

Полная энергия

Полная энергия E определяется как E = γmc ² , где м – масса, c – скорость света.2}}}\\[/latex]

и v — скорость массы относительно наблюдателя. Есть много аспектов полной энергии E , которые мы обсудим — среди них то, как кинетическая и потенциальная энергии включены в E и как E связано с релятивистским импульсом. Но сначала отметим, что в состоянии покоя полная энергия не равна нулю. Скорее, когда v = 0, мы имеем γ = 1, и у объекта есть энергия покоя.

Энергия покоя

Энергия покоя равна E ₀ = мс ² .

Это правильная форма самого известного уравнения Эйнштейна, которое впервые показало, что энергия связана с массой покоящегося объекта. Например, если в объекте запасена энергия, его масса покоя увеличивается. Это также означает, что масса может быть разрушена для высвобождения энергии. Последствия этих первых двух уравнений относительно релятивистской энергии настолько широки, что они не были полностью осознаны в течение нескольких лет после того, как Эйнштейн опубликовал их в 1919 году.07, и экспериментальное доказательство их правильности поначалу не было общепризнанным. Следует отметить, что Эйнштейн действительно понял и описал значения и следствия своей теории.

Пример 1. Расчет энергии покоя: Энергия покоя очень велика

Рассчитайте энергию покоя груза массой 1,00 г.

Стратегия

Один грамм — это небольшая масса — менее половины массы пенни. Мы можем умножить эту массу в единицах СИ на квадрат скорости света, чтобы найти эквивалентную энергию покоя. 92\end{array}\\[/latex]

Преобразование единиц измерения. Учитывая, что 1 кг · м ² /с ² = 1 Дж, мы видим, что энергия массы покоя равна E ₀ = 9,00 × 10 ¹³ Дж.

Обсуждение

Это огромное количество энергии для массы в 1,00 г. Мы не замечаем эту энергию, потому что она вообще недоступна. Энергия покоя велика, потому что скорость света c — большое число, а c ² — очень большое число, так что mc ² огромен для любой макроскопической массы. Энергия массы покоя 9,00 × 10 ¹³ Дж для 1,00 г примерно в два раза превышает энергию, высвобожденную атомной бомбой, сброшенной на Хиросиму, и примерно в 10 000 раз превышает кинетическую энергию большого авианосца. Если будет найден способ преобразования энергии массы покоя в какую-либо другую форму (а все формы энергии могут быть преобразованы друг в друга), то при разрушении массы можно будет получить огромное количество энергии.

Сегодня практическое применение преобразование массы в другую форму энергии , например, в ядерном оружии и атомных электростанциях, хорошо известны. Но примеры существовали и тогда, когда Эйнштейн впервые предложил правильную форму релятивистской энергии, и он действительно описал некоторые из них. Ядерное излучение было обнаружено в предыдущем десятилетии, и оставалось загадкой, откуда берется его энергия. Объяснение заключалось в том, что в некоторых ядерных процессах небольшое количество массы разрушается, а энергия высвобождается и переносится ядерным излучением. Но количество уничтоженной массы настолько мало, что трудно обнаружить отсутствие чего-либо. Хотя Эйнштейн предположил, что это источник энергии в изучаемых в то время радиоактивных солях, прошло много лет, прежде чем было широко признано, что масса может быть преобразована и фактически обычно преобразуется в энергию. (См. рис. 2.)

Рисунок 2. Солнце (а) и паровая электростанция Саскуэханна (б) преобразуют массу в энергию: Солнце посредством ядерного синтеза, электрическая станция посредством ядерного деления. (кредиты: (а) НАСА/Центр космических полетов имени Годдарда, Студия научной визуализации; (б) правительство США)

Из-за связи энергии покоя с массой мы теперь считаем массу формой энергии, а не чем-то отдельным. До работы Эйнштейна не было даже намека на это. Теперь известно, что такое преобразование является источником солнечной энергии, энергии ядерного распада и даже источником энергии, поддерживающей недра Земли горячими.

Накопленная энергия и потенциальная энергия

Что происходит с энергией, запасенной в объекте в состоянии покоя, например, с энергией, переданной в аккумулятор при его зарядке, или с энергией, запасенной в сжатой пружине игрушечного пистолета? Вклад энергии становится частью полной энергии объекта и, таким образом, увеличивает его массу покоя. Вся запасенная и потенциальная энергия становится массой в системе. Почему мы обычно этого не замечаем? На самом деле, сохранение массы (что означает, что общая масса постоянна) было одним из великих законов, подтвержденных 19наука X века. Почему не было замечено, что это неправильно? Пример 2 помогает ответить на эти вопросы.

Пример 2. Расчет массы покоя: небольшое увеличение массы из-за подводимой энергии

Расчетная мощность автомобильного аккумулятора составляет 600 ампер-часов (А · ч) при заряде 12,0 В.

Рассчитайте увеличение в массе покоя такой батареи, когда она переходит от полностью разряженного состояния к полностью заряженному.
На сколько процентов это увеличение, учитывая массу батареи 20,0 кг?

Стратегия

В части 1 мы сначала должны найти энергию, запасенную в батарее, которая равняется тому, что батарея может дать в виде потенциальной электрической энергии. Поскольку PE _elec = qV , мы должны рассчитать заряд q в 600 А·ч, который является произведением тока I и времени t . Затем мы умножаем результат на 12,0 В. Затем мы можем рассчитать увеличение массы батареи, используя Δ E = PE _elec = (Δ м ) c ² . Часть 2 – это простое соотношение, преобразованное в проценты.

Решение для Части 1

Определите известные значения: I ⋅ t = 600 А ⋅ ч; В = 12,0 В; c = 3,00 × 10 ⁸ м/с

Определите неизвестное: Δ м

Выберите подходящее уравнение. PE _elec =(Δ м ) c ²

Переформулируйте уравнение, чтобы найти неизвестное. 92}\end{array}\\[/latex]

Используя преобразование 1 кг · м ² /с ² = 1 Дж, мы можем записать массу как Δ м = 2,88 × 10 ^{− 10} кг.

Решение для Части 2

Определите известные значения: Δ м = 2,88 × 10 ⁻¹⁰ кг; м =20,0 кг

Определите неизвестное: % изменения

Выберите подходящее уравнение. [латекс]\%\текст{ увеличение}=\frac{\Delta{m}}{m}\times100\%\\[/latex]

Подставьте известные значения в уравнение. 9{-9}\%\end{array}\\[/latex]

Обсуждение

Как фактическое увеличение массы, так и процентное увеличение очень малы, так как энергия делится на c ² , очень большое количество. Нам нужно было бы измерить массу батареи с точностью до одной миллиардной доли процента, или 1 части на 10 ¹¹ , чтобы заметить это увеличение. Неудивительно, что изменение массы не так просто наблюдать. На самом деле это изменение массы настолько мало, что мы можем задаться вопросом, как вы можете проверить, что оно реально. Ответ можно найти в ядерных процессах, в которых процент разрушенной массы достаточно велик, чтобы его можно было измерить. Масса топлива ядерного реактора, например, значительно меньше, когда его энергия была использована. В этом случае запасенная энергия высвобождается (превращается в основном в тепло и электричество), а масса покоя уменьшается. Это также имеет место, когда вы используете энергию, хранящуюся в батарее, за исключением того, что запасенная энергия намного больше в ядерных процессах, что делает изменение массы измеримым как на практике, так и в теории. 92\\[/латекс]. Релятивистское выражение для кинетической энергии получается из теоремы о работе-энергии. Эта теорема утверждает, что чистая работа системы переходит в кинетическую энергию. Если наша система начинает с состояния покоя, то теорема о работе-энергии такова: Вт _нетто = KE.

Релятивистски, в состоянии покоя мы имеем энергию покоя E ₀ = mc ² . Работа увеличивает это до полной энергии E = γmc ² . Таким образом, W _NET = E — E ₀ = γ MC ² — MC ² = ( γ .^{. ^{. ^.}}

Релятивистски имеем W _net = KE _rel .

Релятивистская кинетическая энергия.

В неподвижном состоянии имеем 92=\text{KE}_{\text{класс}}\\[/латекс].

Таким образом, фактически релятивистская кинетическая энергия становится такой же, как классическая кинетическая энергия, когда v << c .

Еще интереснее исследовать, что происходит с кинетической энергией, когда скорость объекта приближается к скорости света. Мы знаем, что γ становится бесконечным, когда v приближается к c , так что KE _rel также становится бесконечным, когда скорость приближается к скорости света. (См. рис. 3.) Чтобы разогнать массу до скорости света, требуется бесконечное количество работы (и, следовательно, бесконечное количество подводимой энергии).

Рисунок 3. Этот график зависимости KE _rel от скорости показывает, как кинетическая энергия приближается к бесконечности, когда скорость приближается к скорости света. Таким образом, объект, имеющий массу, не может достичь скорости света. Также показан класс KE , классическая кинетическая энергия, которая подобна релятивистской кинетической энергии при низких скоростях. Обратите внимание, что для достижения высоких скоростей требуется гораздо больше энергии, чем предсказывалось классически.

Скорость света

Ни один объект с массой не может достичь скорости света.

Таким образом, скорость света является предельной скоростью для любой частицы, имеющей массу. Все это согласуется с тем фактом, что скорости меньше c всегда добавляются к меньшему, чем c . Как релятивистская форма кинетической энергии, так и предельная скорость, равная c , были подробно подтверждены в многочисленных экспериментах. Независимо от того, сколько энергии затрачено на ускорение массы, ее скорость может только приближаться, а не достигать скорости света.

Пример 3. Сравнение кинетической энергии: релятивистская энергия с классической кинетической энергией

Электрон имеет скорость v = 0,990 c .

Рассчитайте кинетическую энергию электрона в МэВ.
Сравните это с классическим значением кинетической энергии при этой скорости. (Масса электрона 9,11 × 10 ⁻³¹ кг.)

Стратегия

Выражение для релятивистской кинетической энергии всегда верно, но для Части 1 его необходимо использовать, поскольку скорость очень релятивистская (близкая к с ). Сначала мы рассчитаем релятивистский фактор γ , а затем используем его для определения релятивистской кинетической энергии. Во второй части мы вычислим классическую кинетическую энергию (которая была бы близка к релятивистскому значению, если бы v было меньше нескольких процентов от c ) и увидим, что это не одно и то же.

Решение для Части 1

Определите известные значения: v = 0,990 c ; м = 9,11 × 10 ⁻³¹ кг 9{-13}\text{ J}}\right)\\\text{ }&=&0,251\text{ МэВ}\end{array}\\[/latex]

Обсуждение

Как и следовало ожидать, поскольку скорость составляет 99,0% скорости света, классическая кинетическая энергия значительно отличается от правильного релятивистского значения. Отметим также, что классическое значение намного меньше релятивистского. На самом деле [латекс]\frac{\text{KE}_{\text{rel}}}{\text{KE}_{\text{класс}}}=12,4\\[/latex] здесь. Это некоторое указание на то, как трудно заставить массу двигаться со скоростью, близкой к скорости света. Требуется гораздо больше энергии, чем предсказывалось классически.

Рисунок 4. Национальная ускорительная лаборатория Ферми, недалеко от Батавии, штат Иллинойс, представляла собой коллайдер субатомных частиц, который ускорял протоны и антипротоны до энергии до 1 Тэв (триллиона электронвольт). Круглые пруды возле колец были построены для отвода отработанного тепла. Этот ускоритель был остановлен в сентябре 2011 года. (Источник: Fermilab, Reidar Hahn)

Некоторые люди интерпретируют эту дополнительную энергию как увеличение массы системы, но, как обсуждалось в Relativistic Momentum, это нельзя проверить однозначно. Не вызывает сомнений то, что требуется постоянно возрастающее количество энергии, чтобы приблизить скорость массы к скорости света. Энергия в 3 МэВ очень мала для электрона и может быть достигнута с помощью современных ускорителей частиц. SLAC, например, может ускорять электроны более чем до 50 × 10 ⁹ эВ = 50 000 МэВ.

Есть ли смысл в получении v немного ближе к c, чем 99,0% или 99,9%? Ответ положительный. Делая это, мы многому учимся. Энергия, которая переходит в высокоскоростную массу, может быть преобразована в любую другую форму, в том числе в совершенно новые массы. (См. рис. 4.) Большая часть того, что мы знаем о субструктуре материи и наборе экзотических короткоживущих частиц в природе, была получена таким образом. Частицы ускоряются до чрезвычайно релятивистских энергий и заставляют сталкиваться с другими частицами, создавая совершенно новые виды частиц. Паттерны характеристик этих ранее неизвестных частиц намекают на основную субструктуру всей материи. Эти частицы и некоторые их характеристики будут рассмотрены в разделе «Физика частиц». 92\\[/латекс].

Релятивистски мы можем получить связь между энергией и импульсом, алгебраически манипулируя их определениями. Это производит E ² = ( PC ) ² + ( MC ²) ², где E является релятивистской общей энергией и P является релитивистской моментом. Эта связь между релятивистской энергией и релятивистским импульсом более сложна, чем классическая, но мы можем получить некоторые интересные новые идеи, исследуя ее. Во-первых, полная энергия связана с импульсом и массой покоя. В состоянии покоя импульс равен нулю, и уравнение дает полную энергию как энергию покоя mc ² (так что это уравнение согласуется с приведенным выше обсуждением энергии покоя). Однако по мере ускорения массы ее импульс p увеличивается, что увеличивает общую энергию. При достаточно высоких скоростях член энергии покоя ( mc ²) ² становится пренебрежимо малым по сравнению с членом импульса ( пк ) ²; таким образом, E = пк при чрезвычайно релятивистских скоростях.

Если мы рассмотрим импульс p отличается от массы, мы можем определить значение уравнения нет массы. Если мы возьмем м равным нулю в этом уравнении, то [латекс]E=pc\text{, или }p=\frac{E}{c}\\[/latex]. Этим импульсом обладают безмассовые частицы. В природе встречается несколько безмассовых частиц, в том числе фотоны (это кванты электромагнитного излучения). Другое следствие состоит в том, что безмассовая частица должна двигаться со скоростью c и только на скорости c . Хотя рассмотрение соотношения в уравнении E ² = ( pc ) ² + ( mc ² ) ² , мы можем видеть в деталях, что эта взаимосвязь имеет важное значение в специальной теории относительности.

Стратегии решения проблем относительности

Изучите ситуацию, чтобы определить, что необходимо использовать относительность 92}}}\\[/latex],
количественный релятивистский фактор. Если γ очень близко к 1, то релятивистские эффекты малы и очень мало отличаются от обычно более простых классических вычислений.
Точно определите, что нужно определить в задаче (идентифицируйте неизвестные).
Составьте список того, что дано или может быть выведено из поставленной задачи (укажите известное). Обратите особое внимание на информацию об относительной скорости в .
Перед выполнением каких-либо вычислений убедитесь, что вы понимаете концептуальные аспекты проблемы. Решите, например, какой наблюдатель увидит увеличение времени или сокращение длины, прежде чем подставлять в уравнения. Если вы подумали о том, кто что видит, кто движется вместе с наблюдаемым событием, кто видит правильное время и т. д., вам будет гораздо легче определить, разумен ли ваш расчет.
Определите основной тип вычислений, которые необходимо выполнить, чтобы найти указанные выше неизвестные. Резюме раздела поможет вам определить, задействовано ли сокращение длины, релятивистская кинетическая энергия или какое-либо другое понятие.
Не округлять при вычислении. Как отмечено в тексте, вы должны часто выполнять вычисления со многими цифрами, чтобы увидеть желаемый эффект. Вы можете округлить в самом конце задачи, но не используйте округленное число в последующих вычислениях.
Проверьте ответ, чтобы убедиться, что он разумен: Имеет ли он смысл? Это может быть сложнее для теории относительности, так как мы не сталкиваемся с ней напрямую. Но вы можете искать скорости больше, чем c , или релятивистские эффекты, которые имеют неправильное направление (например, сокращение времени там, где ожидалось расширение).

Проверьте свое понимание

Фотон распадается на пару электрон-позитрон. 2\\[/latex] 9{2}}}}\\[/латекс] .

Энергия покоя равна E ₀ = mc ² , что означает, что масса является формой энергии. Если энергия накапливается в объекте, его масса увеличивается. Массу можно разрушить, чтобы высвободить энергию.

Обычно мы не замечаем увеличения или уменьшения массы объекта, потому что изменение массы очень мало при большом увеличении энергии.

Релятивистская теорема работы-энергии: Вт _нетто = {2}}}}\\[/латекс]. При малых скоростях релятивистская кинетическая энергия сводится к классической кинетической энергии.

Ни один объект с массой не может достичь скорости света, поскольку для ускорения массы до скорости света требуется бесконечное количество работы и бесконечное количество энергии.

Уравнение E ² = ( пк ) ² + ( mc ² ) ² связывает релятивистский момент9 E 9002 и полную энергию
029 стр . При чрезвычайно высоких скоростях энергия покоя мс ² становится незначительной, и E = пк .

Концептуальные вопросы

Как современные теории относительности изменяют классические законы сохранения энергии и сохранения массы?
Что происходит с массой воды в кастрюле, когда она охлаждается, если предположить, что никакие молекулы не улетучиваются и не добавляются? Наблюдается ли это на практике? Объяснять.
Проведите мысленный эксперимент. Ранним утром вы помещаете надутый воздушный шар на весы снаружи. Воздушный шар остается на весах, и вы можете измерить изменения его массы. Изменяется ли масса шарика в течение дня? Обсудите трудности при проведении этого эксперимента.
Масса топлива в ядерном реакторе уменьшается на наблюдаемую величину по мере выделения энергии. Верно ли то же самое для угля и кислорода на обычной электростанции? Если да, то наблюдается ли это на практике для угля и кислорода? Объяснять.
Мы знаем, что скорость объекта с массой имеет верхний предел c . Существует ли верхний предел его импульса? Его энергия? Объяснять.
Учитывая тот факт, что свет движется со скоростью c , может ли он иметь массу? Объяснять.
Если вы используете наземный телескоп для проецирования лазерного луча на Луну, вы можете перемещать пятно по поверхности Луны со скоростью, превышающей скорость света. Нарушает ли это современную относительность? (Обратите внимание, что свет направляется с Земли на Луну, а не через поверхность Луны.)

Задачи и упражнения

Какова энергия покоя электрона, если его масса равна 9,11 × 10 ⁻³¹ кг? Дайте ответ в джоулях и МэВ.
Найдите энергию покоя протона в джоулях и МэВ, если его масса равна 1,67 × 10 ⁻²⁷ кг.
Если энергии покоя протона и нейтрона (двух составляющих ядер) равны 938,3 и 939,6 МэВ соответственно, какова разница в их массах в килограммах?
По оценкам, Большой взрыв, с которого началась Вселенная, высвободил 10 ⁶⁸ Дж энергии. Сколько звезд может создать половина этой энергии, если предположить, что средняя масса звезды составляет 4,00 × 10 ³⁰ кг?
Взрыв сверхновой звезды размером 2,00 × 10 ³¹ кг производит 1,00 × 10 ⁴⁴ кг энергии. а) Сколько килограммов массы преобразуется в энергию при взрыве? (b) Чему равно отношение [латекс]\frac{\Delta{m}}{m}\\[/латекс] разрушенной массы к исходной массе звезды?
(a) Используя данные из Таблицы 1 в Законе о сохранении энергии, рассчитайте массу, преобразованную в энергию при делении 1,00 кг урана. (b) Каково отношение массы, разрушенной к первоначальной массе, [латекс]\frac{\Delta{m}}{m}\\[/latex]?
(a) Используя данные из Таблицы 1 в разделе «Сохранение энергии», рассчитайте количество массы, преобразованной в энергию при синтезе 1,00 кг водорода. (b) Каково отношение массы, разрушенной к первоначальной массе, [латекс]\frac{\Delta{m}}{m}\\[/latex]? (c) Как это соотносится с [латексом]\frac{\Delta{m}}{m}\\[/latex] для деления 1,00 кг урана?
Существует приблизительно 10 ³⁴ Дж энергии, получаемой в результате синтеза водорода в Мировом океане. (а) Если 10 ³³ Дж этой энергии, каково будет уменьшение массы океанов? (б) Насколько большому объему воды это соответствует? (c) Прокомментируйте, составляет ли это значительную долю общей массы океанов.
Мюон имеет энергию массы покоя 105,7 МэВ и распадается на электрон и безмассовую частицу. (а) Если вся потерянная масса будет преобразована в кинетическую энергию электрона, найдите для электрона γ . б) Какова скорость электрона?
π-мезон — это частица, распадающаяся на мюон и безмассовую частицу. π-мезон имеет энергию массы покоя 139,6 МэВ, а мюон имеет энергию массы покоя 105,7 МэВ. Предположим, что π-мезон покоится, и вся недостающая масса идет на кинетическую энергию мюона. С какой скоростью будет двигаться мюон?
(a) Рассчитайте релятивистскую кинетическую энергию автомобиля массой 1000 кг, движущегося со скоростью 30,0 м/с, если скорость света составляет всего 45,0 м/с. (b) Найдите отношение релятивистской кинетической энергии к классической.
Альфа-распад — это ядерный распад, при котором испускается ядро гелия. Если ядро гелия имеет массу 6,80 × 10 ⁻²⁷ кг и ему придана кинетическая энергия 5,00 МэВ, какова его скорость?
(a) Бета-распад — это ядерный распад, при котором испускается электрон. Если электрону придана кинетическая энергия 0,750 МэВ, какова его скорость? (b) Прокомментируйте, как высокая скорость согласуется с кинетической энергией по сравнению с энергией массы покоя электрона.
Позитрон — это версия электрона из антивещества, имеющая точно такую же массу. Когда позитрон и электрон встречаются, они аннигилируют, превращая всю свою массу в энергию. (а) Найдите выделившуюся энергию, предполагая пренебрежимо малую кинетическую энергию до аннигиляции. (b) Если эта энергия передана протону в виде кинетической энергии, какова его скорость? (c) Если эта энергия передана другому электрону в виде кинетической энергии, какова его скорость?
Чему равна кинетическая энергия в МэВ π-мезона, живущего 1,40 × 10 9{2}-1\\[/латекс] . Это означает, что при больших скоростях пк >> мс ² . (b) Является ли E ≈ пк , когда γ = 30,0, как для астронавта, обсуждаемого в парадоксе близнецов?
Один нейтрон космического луча имеет скорость [латекс]0,250c[/латекс] относительно Земли. (а) Какова полная энергия нейтрона в МэВ? (б) Найдите его импульс. (c) Является ли E ≈ pc в этой ситуации? Обсудите с помощью уравнения, данного в части (а) предыдущей задачи.
Чему равно γ для протона с массовой энергией 938,3 МэВ, ускоренного при эффективном потенциале 1,0 ТВ (теравольт) в лаборатории Ферми под Чикаго?
(a) Чему равен эффективный ускоряющий потенциал электронов на Стэнфордском линейном ускорителе, если для них γ = 1,00 × 10 ⁵? (б) Какова их полная энергия (почти такая же, как кинетическая в данном случае) в ГэВ?
(a) Используя данные из Таблицы 1 в разделе «Сохранение энергии», найдите массу, разрушаемую при высвобождении энергии в барреле сырой нефти. (b) Учитывая, что в этих бочках содержится 200 литров, а плотность сырой нефти составляет 750 кг/м ³ , каково отношение разрушенной массы к первоначальной массе, [латекс]\frac{\Delta{m}}{m}\\[/latex]?
(a) Рассчитайте энергию, выделяющуюся при разрушении 1,00 кг массы. (b) Сколько килограммов можно поднять на высоту 10,0 км с помощью этого количества энергии?
Ускоритель Ван де Граафа использует разность потенциалов 50,0 МВ для ускорения заряженных частиц, таких как протоны. а) Какова скорость протона, ускоренного таким потенциалом? (б) Электрон?
Предположим, вы используете в среднем 500 кВт·ч электроэнергии в месяц в своем доме. (a) Как долго вам хватит 1,00 г массы, преобразованной в электрическую энергию с КПД 38,0%? (b) Сколько домов можно было бы снабжать электроэнергией из описанного преобразования массы при скорости 500 кВт·ч в месяц в течение одного года?
(a) Атомная электростанция преобразует энергию ядерного деления в электричество с КПД 35,0%. Сколько массы разрушается за один год, чтобы непрерывно производить 1000 МВт электроэнергии? (b) Считаете ли вы, что можно было бы наблюдать эту потерю массы, если общая масса топлива составляет 10 ⁴ кг?
Ракеты с ядерными двигателями исследовались в течение нескольких лет, прежде чем вопросы безопасности стали первостепенными. (а) Какую часть массы ракеты необходимо уничтожить, чтобы вывести ее на низкую околоземную орбиту, если не учитывать уменьшение силы тяжести? (Примите высоту орбиты 250 км и рассчитайте как кинетическую энергию (классическую), так и необходимую гравитационную потенциальную энергию.) (b) если корабль имеет массу 1,00 × 10 ⁵ кг (100 тонн), какая общая мощность ядерного взрыва в тоннах тротила нужна?
Солнце производит энергию со скоростью 4,00 × 10 ²⁶ Вт путем синтеза водорода. (а) Сколько килограммов водорода подвергается синтезу каждую секунду? (b) Если Солнце на 90,0 % состоит из водорода, и половина его может подвергнуться синтезу до того, как Солнце изменит свой характер, как долго оно сможет производить энергию при нынешнем уровне? (c) Сколько килограммов массы теряет Солнце в секунду? (d) Какую часть своей массы он потеряет за время, указанное в пункте (b)?
Необоснованные результаты. Протон имеет массу 1,67 × 10 ⁻²⁷ кг. Физик измеряет полную энергию протона как 50,0 МэВ. а) Чему равна кинетическая энергия протона? (б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
Создайте свою собственную задачу. Рассмотрим высокорелятивистскую частицу. Обсудите, что подразумевается под термином «высокорелятивистский». (Обратите внимание, что это отчасти означает, что частица не может быть безмассовой.) Постройте задачу, в которой вы вычисляете длину волны такой частицы и показываете, что она почти совпадает с длиной волны безмассовой частицы, такой как фотон с той же энергией. Среди вещей, которые следует учитывать, — энергия покоя частицы (это должна быть известная частица) и ее полная энергия, которая должна быть большой по сравнению с ее энергией покоя.
Создайте свою собственную задачу. Рассмотрите астронавта, летящего к другой звезде с релятивистской скоростью. Постройте задачу, в которой вы вычисляете время полета по наблюдениям на Земле и по наблюдениям космонавта. Также рассчитайте количество массы, которое должно быть преобразовано в энергию, чтобы космонавт и корабль достигли пройденной скорости. Среди вещей, которые следует учитывать, — расстояние до звезды, скорость и масса космонавта и корабля. Если ваш инструктор не дал вам иных указаний, не включайте энергию, отдаваемую другим массам, например, ракетному топливу. 9{2}}}}[/latex]
Избранные решения задач и упражнений
1. 8,20 × 10 ⁻¹⁴ Дж; 0,512 МэВ
3. 2,3 × 10 ⁻³⁰ кг
5. (а) 1,11 × 10 ²⁷ кг; б) 5,56 × 10 ⁻⁵
7,7,1 × 10 ⁻³ кг
7,1 × 10 ⁻³
Отношение больше для водорода.
9. (а) 208; (б) 0,999988 в
11. (а) 6,92 × 10 ⁵ Дж; (б) 1,54
9{2}-1\end{array}\\[/latex]
(b) да
19. 1,07 × 10 ³
21. (a) 6,56 × 10 ⁻⁸ кг; (б) 4,37 × 10 ⁻¹⁰
23. (а) 0,314 в ; (b) 0,99995 c
25. (a) 1,00 кг; (b) Такую большую массу можно было бы измерить, но, вероятно, ее нельзя было бы наблюдать, просто глядя, потому что она составляет 0,01% от общей массы.
27. (а) 6,3 × 10 ¹¹ кг/с; (б) 4,5 × 10 ¹⁰ лет; (в) 4,44 × 10 ⁹ кг; (d) 0,32%
8 способов увидеть теорию относительности Эйнштейна в реальной жизни
Спутник GPS Навстар-2Ф (Изображение предоставлено ВВС США)
Сформулированная Альбертом Эйнштейном начиная с 1905 года, теория относительности объясняет поведение объектов в пространстве и времени, и ее можно использовать для предсказания таких вещей, как существование черных дыр , искривление света из-за гравитация и поведение планет на своих орбитах.
Теория обманчиво проста. Во-первых, не существует «абсолютной» системы отсчета. Каждый раз, когда вы измеряете скорость объекта, его импульс или то, как он воспринимает время, это всегда связано с чем-то другим. Во-вторых, скорость света одинакова, независимо от того, кто ее измеряет или с какой скоростью движется измеряющий ее человек. В-третьих, ничто не может двигаться быстрее света.
Выводы из самой известной теории Эйнштейна глубоки. Если скорость света всегда одинакова, это означает, что астронавт, движущийся очень быстро относительно Земли , будет измерять секунды медленнее, чем земной наблюдатель. Время существенно замедляется для космонавта — явление, называемое замедлением времени .
Связанный: Что произошло бы, если бы скорость света была намного меньше?
Любой объект в большом гравитационном поле ускоряется, поэтому он также испытывает замедление времени. Тем временем космический корабль астронавта испытывает сокращение длины , а это значит, что если вы сфотографируете космический корабль во время его полета, он будет выглядеть так, как будто он «сплющен» в направлении движения. Однако космонавту на борту все казалось бы нормальным. Кроме того, с точки зрения людей на Земле масса космического корабля могла бы увеличиться.
Но вам не обязательно нужен космический корабль , движущийся с околосветовой скоростью , чтобы увидеть релятивистские эффекты. Действительно, есть несколько примеров относительности, которые мы можем наблюдать в нашей повседневной жизни и технологиях, которые мы используем сегодня, которые демонстрируют, что Эйнштейн был прав. Вот несколько способов увидеть относительность в действии.
Электромагниты
Крупный план рабочего, держащего электромагнитную катушку на заводе электромагнетиков. (Изображение предоставлено: Monty Rakusen через Getty Images)
Магнетизм — это релятивистский эффект, и вы можете увидеть это с помощью генераторов. Если вы возьмете проволочную петлю и проведете ее через магнитное поле, вы получите электрический ток. На заряженные частицы в проводе действует изменяющееся магнитное поле , которое заставляет некоторые из них двигаться и создает ток.
А теперь представьте провод в покое и вообразите, что магнит движется. В этом случае заряженные частицы в проводе (электроны и протоны) больше не двигаются, поэтому магнитное поле не должно на них влиять. Но это происходит, и ток все еще течет. Это показывает, что нет привилегированной системы отсчета.
Томас Мур, профессор физики в Колледже Помона в Клермонте, Калифорния, использует принцип относительности для демонстрации закона Фарадея , который гласит, что изменяющееся магнитное поле создает электрический ток.
«Поскольку это основной принцип трансформаторов и электрических генераторов, любой, кто использует электричество, испытывает эффекты относительности», — сказал Мур Live Science.
Электромагниты тоже работают по теории относительности. Когда постоянный ток электрического заряда течет по проводу, электроны дрейфуют через материал. Обычно провод кажется электрически нейтральным, без положительного или отрицательного заряда, потому что в проводе примерно одинаковое количество протонов (положительных зарядов) и электронов (отрицательных зарядов). Но если положить рядом другой провод с постоянным током, провода притягиваются или отталкиваются друг от друга, в зависимости от направления, в котором движется ток, по данным физиков из Университета Иллинойса в Урбана-Шампейн (открывается в новой вкладке).
Если предположить, что токи движутся в одном направлении, электроны во втором проводе неподвижны по сравнению с электронами в первом проводе. (Это предполагает, что токи примерно одинаковой силы.) Между тем, протоны в обоих проводах движутся по сравнению с электронами в обоих проводах. Из-за релятивистского сокращения длины они кажутся более близко расположенными, поэтому на длину провода приходится больше положительного заряда, чем отрицательного. Поскольку как заряды отталкиваются, так и два провода отталкиваются.
Токи в противоположных направлениях приводят к притяжению, потому что по сравнению с первым проводом электроны в другом проводе более скучены, что создает общий отрицательный заряд, по данным Университета Иллинойса в Урбана-Шампейн (открывается в новая вкладка). Тем временем протоны в первом проводе создают суммарный положительный заряд, и противоположные заряды притягиваются.
GPS-навигация
GPS-навигация — отличный пример релятивистского замедления времени. (Изображение предоставлено: BlackJack3D через Getty Images)
Согласно PhysicsCentral , чтобы GPS-навигация вашего автомобиля функционировала так точно, спутники должны учитывать релятивистские эффекты. Это потому, что хотя спутники и не движутся близко к скорости света, они все равно движутся довольно быстро. Спутники также посылают сигналы наземным станциям на Земле. Эти станции (а также технология GPS в автомобиле или смартфоне) испытывают более высокие ускорения из-за гравитации, чем спутники на орбите.
Чтобы добиться такой высокой точности, спутники используют часы с точностью до нескольких наносекунд (миллиардных долей секунды). Поскольку каждый спутник находится на высоте 12 600 миль (20 300 километров) над Землей и движется со скоростью около 6 000 миль в час (10 000 км/ч), существует релятивистское замедление времени , которое увеличивается примерно на 4 микросекунды каждый день. Добавьте сюда эффекты гравитации, и эффект замедления времени увеличится примерно до 7 микросекунд (миллионных долей секунды).
Разница весьма реальна: если бы не учитывались никакие релятивистские эффекты, устройство GPS, которое сообщает вам, что до следующей заправки 0,8 км, расстояние до следующей заправки составило бы 5 миль (8 км), согласно в Центр физики.
Желтый цвет золота
(Изображение предоставлено Джонатаном Ноулзом через Getty Images)
Большинство металлов блестят, потому что электроны в атомах прыгают с разных энергетических уровней или «орбиталей». Некоторые фотоны, попавшие на металл, поглощаются и переизлучаются, хотя и с большей длиной волны. Однако большая часть видимого света отражается.
Золото является тяжелым элементом , поэтому внутренние электроны движутся достаточно быстро, чтобы релятивистское увеличение массы и сокращение длины было значительным, в соответствии с (открывается в новой вкладке) заявление (открывается в новой вкладке) из Гейдельбергского университета в Германии. В результате электроны вращаются вокруг ядра более короткими путями с большим импульсом. Электроны на внутренних орбиталях несут энергию, близкую к энергии внешних электронов, а длины волн, которые они поглощают и отражают, больше. Более длинные волны света означают, что часть видимого света, который обычно отражается, поглощается, и этот свет находится в синей части спектра. Белый свет это смесь всех цветов радуги , но в случае с золотом, когда свет поглощается и переизлучается, длина волны обычно больше. Это означает, что в смеси световых волн, которые мы видим, меньше синего и фиолетового. Поскольку длина волны желтого, оранжевого и красного света больше, чем у синего, золото кажется желтоватым, согласно BBC (открывается в новой вкладке).
Стойкость золота к коррозии
Золото отлично подходит для использования в ювелирных изделиях, хотя изделия из чистого золота встречаются редко. (Изображение предоставлено Питером Дазели через Getty Images)
Релятивистский эффект на электроны золота также является одной из причин, по которой золото не подвергается коррозии и легко не реагирует ни с чем другим, согласно статье 1998 года в журнале Gold Bulletin .
У золота только один электрон на внешней оболочке, но оно не так реактивно, как кальций или литий. Вместо этого, поскольку электроны в золоте «тяжелее», чем они должны быть, поскольку они движутся со скоростью, близкой к скорости света, увеличивая свою массу, они удерживаются ближе к атомному ядру. Это означает, что самый дальний электрон вряд ли может вообще с чем-либо реагировать; с такой же вероятностью он может быть среди электронов, близких к ядру.
Жидкая ртуть
Ртуть используется в ЖК-экранах и мониторах. (Изображение предоставлено Питером Кейдом через Getty Images)
Меркурий также является тяжелым атомом, в котором электроны удерживаются близко к ядру из-за их скорости и последующего увеличения массы. Связи между атомами ртути слабы, поэтому ртуть плавится при более низких температурах и обычно является жидкостью, когда мы ее видим, согласно Chemistry World .
Ваш старый телевизор
Электронно-лучевая трубка, используемая в старом аналоговом осциллографе в лаборатории. (Изображение предоставлено: albln через Getty Images)
Примерно до начала 2000-х большинство телевизоров и мониторов имели экраны с электронно-лучевой трубкой. Электронно-лучевая трубка работает, запуская электроны на поверхность люминофора с помощью большого магнита. Каждый электрон образует подсвеченный пиксель, когда он попадает на заднюю часть экрана, и электроны вспыхивают, заставляя изображение двигаться со скоростью до 30% скорости света. Релятивистские эффекты заметны, и когда производители формировали магниты, они должны были учитывать эти эффекты, согласно PBS News Hour (открывается в новой вкладке).
Свет
Изображение гигантской галактики UGC 2885, полученное космическим телескопом Хаббл. (Изображение предоставлено NASA/ESAB. Holwerda (Университет Луисвилля))
Исаак Ньютон предположил, что существует абсолютная система покоя или внешняя совершенная система отсчета, с которой мы могли бы сравнить все другие системы отсчета. Если бы он был прав, нам пришлось бы придумать другое объяснение света, потому что его бы вообще не было.
«Не было бы не только магнетизма, но и света, потому что относительность требует, чтобы изменения в электромагнитном поле происходили с конечной скоростью, а не мгновенно», — сказал Мур. «Если бы теория относительности не навязывала это требование… изменения в электрических полях сообщались бы мгновенно… вместо электромагнитных волн, и и магнетизм, и свет были бы не нужны». 92 — солнце и остальные звезды не светят. Согласно Университета штата Огайо , в центре нашей родительской звезды интенсивные температуры и давления постоянно сжимают четыре отдельных атома водорода в один атом гелия . Масса одного атома гелия лишь немногим меньше массы четырех атомов водорода. Что происходит с дополнительной массой? Он напрямую преобразуется в энергию, которая проявляется в виде солнечного света на нашей планете.
Дополнительные ресурсы
Узнайте больше о том, как теория относительности влияет на изучение удаленных космических объектов (открывается в новой вкладке) , от НАСА.
См. , как теория относительности становится важной (открывается в новой вкладке) для ускорителей частиц, от Fermilab.
Исследуйте историю теории относительности Эйнштейна и ее многочисленные подтвержденные предсказания от Европейского космического агентства.
Эта статья была обновлена 22 марта 2022 г. автором Live Science Адамом Манном.
Джесси Эмспак — автор статей для Live Science, Space.com и Toms Guide. Он занимается физикой, здоровьем человека и общей наукой. Джесси имеет степень магистра искусств Калифорнийского университета, Школы журналистики Беркли и степень бакалавра искусств Университета Рочестера. Джесси провел годы, освещая финансы, и набился зубами в местных газетах, работая с местными политиками и полицией. Джесси любит вести активный образ жизни и имеет черный пояс третьей степени по каратэ, что означает, что теперь он знает, как многому ему еще предстоит научиться.
При участии
Adam MannLive Science Contributor
Релятивистская масса
предыдущая главная следующая
Майкл Фаулер, Университет Вирджинии
История до сих пор: краткий обзор
Первое последовательное утверждение того, что физики теперь называют теорией относительности было наблюдение Галилея почти четыреста лет назад, что если вы находитесь в большую закрытую комнату, чего нельзя было сказать, наблюдая за движением вещей — живые вещи, брошенные вещи, капающие жидкости — будь то комната находилась в покое, скажем, в здании или под палубой большого движущегося корабля. с постоянной скоростью. Более технически (но на самом деле говоря одно и то же!) мы бы сказали, что законы движения одинаковы в любой инерциальной системе отсчета. Это то есть эти законы действительно описывают только относительную позицию и скорость. В частности, они не выделяют специальную инерциальную систему отсчета как ту, которая «реально покоится». Позже все это было записано более формально, в терминах преобразований Галилея . Используя эти простые линейные уравнения, движение анализируются с точки зрения положений и скоростей в одной инерциальной системе отсчета. переводится на любой другой. Когда после Галилея Ньютон писал Согласно его трем законам движения, они, конечно, были инвариантны относительно Галилея. преобразований и действителен в любой инерциальной системе отсчета.
Около двухсот лет назад стало ясно, что свет — это не просто поток частиц (как Ньютон думал), но проявил определенные волнообразные свойства. Это привело, естественно, к вопросу о том, что, точно, махал, и по общему мнению, пространство было заполнено эфиром , и световые волны были рябью в этом всепроникающем эфире, подобно звуку. волны в воздухе. Открытие Максвелла, что уравнения, описывающие электромагнитные явления, имели волнообразные решения, и предсказал скорость, совпадающую с измеренной скоростью света, предложил что электрические и магнитные поля были напряжениями или напряжениями в эфире, и Уравнения Максвелла, по-видимому, были точно правильными только в системе отсчёта. котором эфир находился в покое. Однако, очень точные эксперименты, которые должны были быть в состоянии обнаружить этот эфир все не удалось.
Около ста лет назад Эйнштейн предположил, что, возможно, все законы физики были одинаковыми в во всех инерциальных системах отсчета, обобщая систему Галилея заявления о движении, чтобы включить недавно открытые законы электричества и магнетизма. Это бы подразумевают, что не может быть специальной системы «реально покоящегося» даже для легких распространения и, следовательно, нет эфира. Этот — очень привлекательная и очень простая концепция: одни и те же законы действуют во всех фреймах. Что может быть разумнее? Однако, как мы видели, это приводит к столкновению с некоторыми представлениями о пространстве и времени, глубоко укоренившимися у всех, кто сталкивается с это впервые. Центральный предсказание заключается в том, что, поскольку скорость света следует из законов физики (уравнения Максвелла) и несколько простых электростатических и магнитостатических экспериментов, которые явно не зависят от кадра , скорость света одинакова во всех инерционные рамы . То есть, скорость конкретной вспышки света всегда будет измеряться как 3×10 ⁸ метров в секунду, даже если их измеряют разные быстро движущиеся наблюдатели относительно друг друга, где каждый наблюдатель измеряет скорость вспышки относительно самого себя. Тем не менее, эксперименты снова и снова показывают, что элегантная проницательность Эйнштейна верна, и глубоко укоренившиеся убеждения всех ошибочны.
Мы подробно обсудили кинематические следствия теории Эйнштейна. постулат: как измеряется положение, время и скорость в одном кадре соотносятся с таковыми в другом, и насколько очевидны парадоксы могут быть разрешены тщательным анализом. Однако до сих пор мы мало думали о динамика. Мы знаем, что законы движения Ньютона были инвариантны при преобразования Галилея между инерциальными системами отсчета. Теперь мы знаем, что преобразования Галилея на самом деле неверно , за исключением низкоскоростного нерелятивистского предела. Поэтому нам лучше внимательно изучить законы движения Ньютона. в свете наших новых знаний.
Ньютона Пересмотренные законы
Ньютона Первый закон, принцип инерции, согласно которому объект не подвержен никакому внешнему силы будут продолжать двигаться прямолинейно с постоянной скоростью, одинаково справедливо в специальной теории относительности. Действительно, это является определяющим свойством инерциальной системы отсчета, что это является истинным, и содержанием специальной теории относительности являются преобразования между такими системами отсчета.
Ньютона Второй закон, сформулированный в виде сила = масса х ускорение, не может быть верным, поскольку это стоит в специальной теории относительности. Это следует из полученной нами формулы сложения скоростей. Представьте себе ракету, имеющую много ступеней, каждая достаточно для разгона оставшейся части ракеты (включая неиспользуемые ступени) до c/2 из покоя. Мы могли бы уволить их одного за другим в тщательно рассчитанный способ создания постоянной большой силы на ракете, которая доведут его до c/2 при первом обжиге. Если ускорение продолжалось, ракета очень скоро превысит скорость света. Но мы знаем из сложения скоростей формула, что на самом деле ракета никогда не достигает c. Очевидно, второй закон Ньютона нуждается в уточнении.
Ньютона Третий закон, действие = противодействие, также имеет проблемы. Рассмотрим некоторую силу притяжения между двумя быстро движущиеся тела. Как их расстояние друг от друга меняется, как и сила притяжения. У нас может возникнуть соблазн сказать, что сила A на B противоположно силе B на A , при каждом момент времени, но это подразумевает одновременных измерений в два тела на некотором расстоянии друг от друга, и если это произойдет в А инерционная рама, ее не будет в B -х.
Законы сохранения
Третий закон нерелятивистской ньютоновской физики говорит нам, что два взаимодействующие тела ощущают равные, но противоположные силы от взаимодействия. Следовательно, согласно второму закону, скорость изменение количества движения одного из тел равно и противоположно импульсу другое тело, таким образом, общая скорость изменения импульса системы вызванное взаимодействием, равно нулю. Следовательно, для любых закрытая динамическая система (без внешних сил) общая импульс никогда не меняется . Это закон сохранения импульса . Оно делает , а не зависят от деталей сил взаимодействия между тела, только то, что они равны и противоположны.
Другим важным динамическим законом сохранения является закон сохранения энергии. Это не было полностью сформулировано до тех пор, пока Ньютона, когда стало ясно, что, например, тепловыделение от трения может количественно объяснить очевидную потерю кинетического плюс потенциального энергии в реальных динамических системах.
Хотя эти законы сохранения были первоначально сформулированы в Ньютоновское мировоззрение, их весьма общий характер подсказали Эйнштейну, что они может иметь более широкое действие. Следовательно, в качестве рабочей гипотезы он предположил, что они выполняются во всех инерциальных кадров и исследовал последствия. Мы придерживаемся такого подхода.
Сохранение импульса на бильярдном столе
В качестве разминки рассмотрим сохранение импульса для столкновение двух шаров на бильярдном столе. Проводим мелом линию посередине бильярдный стол и бросайте шары рядом с мелом, но с противоположных сторон линии с обоих концов с одинаковой скоростью, поэтому они попадут в середину с скользящий удар, который повернет их скорости на небольшой угол. Другими словами, если изначально мы говорим их (равные величина, противоположное направление) скорости были параллельны направлению x — мел линия — затем после при столкновении они также будут иметь равные и противоположно малые скорости в направлении y. (Скорости в направлении x уменьшится очень немного).
Симметричное столкновение космического корабля
Теперь давайте повторим упражнение в большом масштабе. Предположим, где-то в космосе, вдали от гравитационные поля, мы натянули струну длиной в миллион миль. (Это может быть между нашими двумя часами в эксперимент с замедлением времени). Эта строка соответствует меловой линии на бильярдном столе. Допустим теперь у нас есть два одинаковых космических корабля сближаются с равными и противоположными скоростями параллельно струна с двух концов струны, направленная так, чтобы они слегка скользящее столкновение, когда они встречаются посередине. Это видно из симметрии ситуация, при которой импульс сохраняется в обоих направлениях. В частности, скорость, с которой один космический корабль удаляется от струны после столкновения — ее у — скорость — равна и противоположно скорости, с которой другой удаляется от струны.
А теперь представьте, что это столкновение наблюдал кто-то в одном из космические корабли, назовите его A . (Запомнить, импульс должен сохраняться в во всех инерциальных системах отсчета — они все эквивалентно — есть ничего особенного в системе отсчета, в которой струна покоится.) Перед столкновением он видит струну двигаясь очень быстро у окна, скажем, на несколько метров. После столкновения он видит, что строка удаляясь, скажем, со скоростью 15 метров в секунду. Это потому, что космический корабль выбрал со скоростью, перпендикулярной струне, 15 м/с. Между тем, поскольку это совершенно симметричная ситуация, наблюдатель на космическом корабле B наверняка сделает вывод что ее космический корабль удалялся от струны со скоростью 15 метров в секунду, как Что ж.
Насколько он симметричен?
Ключевой вопрос: с какой скоростью наблюдатель на космическом корабле А видит космический корабль B будет удаляться от струны? Допустим, что относительно космического корабля А , космический корабль B удаляется (в направлении x) на 0,6c. Во-первых, напомним, что расстояния, перпендикулярные направление движения не лоренцево сокращение. Следовательно, когда наблюдатель на космическом корабле B говорит, что она переместилась на 15 метров дальше от веревки за одну секунду интервал, наблюдатель, наблюдающий за этим движением с космического корабля A , согласен насчет 15 метров, но не соглашусь на одну секунду! Он скажет ее часы идут медленно, так что по его часам 1,25 секунды придется прошло, когда она пройдет 15 метров в y — направление.
Отсюда следует, что в результате замедления времени это столкновение, если смотреть с космический корабль A не вызывает ли , а не , равные и противоположные скорости для два космических корабля в y-направлении. Первоначально оба космических корабля двигались параллельно оси x — импульс в направлении y был нулевым. Рассмотрим сохранение импульса в направлении y в инерциальная система отсчета, в которой A изначально находился в состоянии покоя. Наблюдатель в этой системе отсчета, измеряющий y-скорости после столкновения, найдет А двигаться со скоростью 15 метров в секунду, B двигаться со скоростью -0,8 x 15 метров в секунду в направлении Y. Итак, как мы можем утверждать, что всего ноль импульс в y-направлении после столкновения, когда идентичные космические корабли не имеют равные и противоположные скорости?
Эйнштейн спасает закон сохранения импульса
Эйнштейн был настолько уверен, что закон сохранения импульса должен соблюдаться всегда, что он спас его смелой гипотезой: масса объекта должна зависеть от его скорость! На самом деле масса должна увеличиваться со скоростью таким образом, чтобы компенсировать меньшую скорость в направлении Y, возникающую из-за времени расширение. То есть, если объект в покое имеет массу m0, а при движении со скоростью v должна иметь массу
m=m01−v2/c2
сохранить y -направление импульс.
Обратите внимание, что это незаметно небольшой эффект при обычных скоростях, но как объект приближается к скорости света, масса увеличивается без ограничений!
Конечно, мы взяли здесь очень частный случай: особый вид столкновение. Читатель вполне может задаться вопросом если бы та же коррекция массы работала и при других типах столкновений, например прямолинейное столкновение, при котором тяжелый предмет наезжает сзади на более легкий предмет. Алгебра проста, хотя и утомительна, и обнаружено, что этот поправочный коэффициент массы действительно обеспечивает импульс сохранение для любого столкновения во всех инерциальных системах отсчета.
Упражнение : проверьте это для прямолинейное столкновение.
Реальная масса
Увеличивается ли со скоростью
Решить, что массы объектов должны зависеть от скорости, как это кажется тяжелым цена за спасение сохранения импульса! Тем не менее, это прогноз, который не трудно проверить опытным путем. Первое подтверждение пришло в 1908 году, когда была измерена масса быстрых электронов в вакуумная труба. В самом деле, электроны в старомодные цветные телевизионные трубки примерно на полпроцента тяжелее электронов на покоя, и это необходимо учитывать при расчете магнитных полей, используемых для направлять их к экрану.
Намного драматичнее, современные ускорители частиц очень мощные электрические поля используются для ускорения электронов, протонов и других частиц. На практике установлено, что эти частицы становиться все тяжелее и тяжелее по мере приближения к скорости света, и, следовательно, необходимо все большие и большие силы для дальнейшего ускорения. Следовательно, скорость света является естественной абсолютное ограничение скорости. Частицы разгоняются до скоростей, при которых их масса в тысячи раз превышает их масса, измеренная в состоянии покоя, обычно называемая «массой покоя».
…Или?
На самом деле среди физиков продолжаются споры относительно этой концепции релятивистской массы. Спор во многом семантический: никто не сомневается в правильности выражение для импульса частицы с массой покоя m , движущейся со скоростью v→ , равно p→=m1−v2/c2v→. Но особенно физики элементарных частиц, многие из которые проводят свою жизнь, измеряя массы покоя частиц с большой точностью, не хочется писать это как p→=mrelv→. Им не нравится идея переменной масса. С одной стороны, это может дать такое впечатление, что по мере ускорения частица раздувается в размерах или, по крайней мере, ее внутренняя структура как-то видоизменяется. В Дело в том, что релятивистская частица просто подвергается лоренцеву сжатию вдоль направление движения, как и все остальное. Он переходит от сферической формы к дискообразная форма с одинаковым поперечным радиусом.
Так как же понимать это «увеличение массы»? Как обычно, Эйнштейн был прав: он заметил что каждая форма энергии обладает инерцией. Сама кинетическая энергия имеет инерция . Теперь «инерция» является определяющим свойство массы: чем больше инерция, тем труднее ускоряться, данная сила ускоряет это меньше .. Другое фундаментальное свойство массы заключается в том, что она притягивается гравитационно. Делает ли эта кинетическая энергия что? Чтобы увидеть ответ, рассмотрите шар, наполненный газом. (И давайте предположим, что взаимодействие между молекулами незначительно, верно для разбавленного газа. ) Сфера газ будет генерировать сферически симметричное гравитационное поле вне себя, прочность пропорциональна общей массе. Если мы теперь нагреем газ, частицы газа будут иметь это увеличенное (релятивистская) масса, соответствующая их повышенной кинетической энергии, и пропорционально увеличится внешнее гравитационное поле. (В этом тоже никто не сомневается.)
Итак, «релятивистская масса» действительно имеет два основных свойства массы: инерция и гравитационное притяжение. (Как станет ясно из следующего лекциях, эта релятивистская масса есть не что иное, как полная энергия, а остальные Сама масса теперь рассматривается как «энергия покоя».)
Сноска : математически сложной обработки, следует добавить, что масса покоя играет важную роль как я вариант при переходе с одного кадра ссылка на другой, но « релятивистский Масса «, используемая здесь, на самом деле является лишь первой составляющей (энергией) четырехмерный вектор энергии-импульса частицы, поэтому , а не является инвариантом Лоренца.
Сохранение массы и энергии: кинетическая энергия и масса для очень быстрых Частицы
Как все слышали, в специальной теории относительности масса и энергия не сохраняясь отдельно, в определенных ситуациях масса m может быть преобразована в энергию E=mc2. Эта эквивалентность тесно связана с как мы увидим, масса увеличивается со скоростью. Предположим, что постоянная сила F ускоряет частицу с массой покоя m0 по прямой. Работа, совершаемая силой при ускорении частица, когда она проходит расстояние d, равна Fd, и эта работа дала кинетическую частицу энергия.
В качестве разминки вспомните элементарный вывод кинетической энергии 12mv2 обычного нерелятивистского (т.е. медленно движущийся) объект массой м . Предположим, он начинается с отдыха. Затем по истечении времени t он прошел расстояние d=12at2 и v=at. Согласно второму закону Ньютона, F=ma, работа силы Fd=mad=12ma2t2=12mv2.
Это не сработает, если масса меняется, потому что второй закон Ньютона не всегда F=ma, для переменной массы это
F=dp/dt,
сила = скорость изменения импульса, и если масса изменяет импульс изменяется даже при постоянной скорости. (Вообще-то так Ньютон написал закон.)
Поучительный крайний случай — кинетическая энергия частица, движущаяся со скоростью, близкой к скорости света, как это делают частицы в ускорители. В этом режиме изменение скорости с увеличением импульса ничтожно мала! Вместо этого
F=dpdt=d(mv)dt≅dmdtc
, где, как обычно, c – скорость света. Вот что происходит в частице ускоритель для заряженной частицы в постоянном электрическом поле, с F=qE.
Так как частица движется со скоростью очень близкой к c, за время dt она будет двигаться cdt и сила будет совершать работу Fcdt. Уравнение выше можно переписать как
Fcdt=(dm)c2.
Таким образом, энергия dE расходуется ускоряющей силой за время dt приводит к увеличению массы, а dE=(dm)c2. При условии, что скорость близка к c, это, конечно, можно интегрировать в отличное приближение, чтобы связать конечное изменение массы частицы с энергией расходуется на его ускорение.
Кинетическая энергия и масса медленных частиц
Напомним, что для сохранения импульса во всех инерциальных системах отсчета мы имели предположить увеличение массы со скоростью в 1/1−v2/c2 раз. Этот обязательно подразумевает, что даже медленно движущийся объект имеет крошечное увеличение массы если он приводится в движение .
Как это увеличение массы связано с кинетической энергией? Рассмотрим частицу с массой покоя m0, движущуюся со скоростью v, намного меньшей скорости света. Его кинетическая энергия E=12m0v2, как обсуждалось выше. Его масса равна m0/1−v2/c2, что мы можем записать как m0+dm, поэтому dm — это крошечное увеличение массы, которое, как мы знаем, должно произойти. Легко вычислить дм.
Для v/c≪1 мы можем сделать приближения
1−v2/c2≅1−12v2/c2
и
11−12v2/c2≅1+12v2/c2.
Итак, для v/c≪1,
m(v)≅m0(1+12v2/c2)dm≅(12m0v2)/c2=KE/c2.
Опять же, увеличение массы dm связано с кинетической энергией KE по KE = (dm)c2. Рассмотрев два простых случая, мы готов вывести общий результат, справедливый во всем диапазоне возможных скорости.
Кинетическая энергия и масса частиц произвольной скорости
В двух предыдущих разделах мы показали, что (в двух предельных случаях), когда сила работает, чтобы увеличить кинетическую энергию частицы, она также вызывает релятивистская масса частицы увеличится на величину, равную увеличению энергия, деленная на c2. На самом деле этот результат в точности верен для весь диапазон скоростей от нуля до сколь угодно близкой к скорости света, т.к. мы сейчас продемонстрируем.
Для частицы с массой покоя m0, ускоряющейся по прямой (из состояния покоя) под действием постоянной силы F,
F=ddt(mv)=dmdtv+mdvdt=m0(1−v2/c2)3/2v2c2dvdt+m0(1−v2/c2)1/2dvdt=m0(1−v2/c2)3/2dvdt.
Таким образом, работа, выполненная при перемещении частицы на расстояние dx , равна дт.
Таким образом, полная работа, выполненная в состоянии покоя,— кинетическая энергия — равна:
∫Fdx=∫m0(1−v2/c2)3/2vdv=(m−m0)c2.
(Интеграл легко сделать, сделав замену y=v2/c2. )
Итак, мы видим, что в общем случае работа, совершенная над телом, по определению его кинетическая энергия как раз равна увеличению его массы, умноженному на c2.
Чтобы понять, почему этого не замечают в повседневной жизни, попробуйте пример, такой как реактивный самолет весом 100 тонн, движущийся со скоростью 2000 миль в час. 100 тонн это 100000 кг, 2000 миль в час это около 1000 метров в секунду. Это кинетическая энергия 12 мв2 ½,10 ¹¹ джоулей, но соответствующее изменение массы самолета уменьшается на коэффициент c2=9⋅1016, что дает фактическое увеличение массы примерно на половину миллиграмм, не слишком легко обнаружить!
Обозначения:
м и м ₀
Как указывалось ранее, мы используем m ₀ для обозначения «массы покоя» объект, и m для обозначения его релятивистской массы, m = m0/1−v2/c2.
В этих обозначениях мы следуем фейнмановскому . Крейн и Типлер, напротив, используют m для масса покоя . Используя м , как мы дает более точные формулы для импульса и энергии, p→=mv→, E=mc2, но не без опасностей. Нужно помнить, что м это а не константа, но функция скорости. Также, надо помнить что релятивистская кинетическая энергия равна ( m — m ₀ ) c ² , и не равно ½ mv ² , даже с релятивистской массой.
Если мы используем m для масса покоя , как обычно делают физики элементарных частиц, мы должны написать
p→=mv→1−v2/c2, E=mc21−v2/c2.
предыдущая главная следующая
Релятивистская масса или масса покоя? | Статьи
Philip Freeman, учитель в средней школе Ричмонда (Ричмонд Б.К.), исполнительный член BCAPT
[email protected]
9068. масса объекта зависит от его скорости ( м = γм ₀ ). Однако, если вы побольше почитаете современную физику, вы скоро столкнетесь с идеей, что это плохая концепция. Почему? Что не так с термином «релятивистская масса»? Некоторые ответы на это физические, некоторые идеологические. Вот обзор аргументов за и против релятивистской массы.
Термины
Одна из проблем, связанных с обсуждением массы в этом споре, заключается в том, что трудно даже вести обсуждение, когда обсуждаются термины, особенно масса . В целях этого обсуждения я буду называть массу объекта в его собственной системе отсчета (которую одна школа желает называть просто массой) как «массу покоя» и изменяющуюся массу из-за системы отсчета (которую первая школа хочет изгнать, а другая школа склонна называть массу просто «релятивистской массой».
Что не так с релятивистской массой?
Физическая проблема заключается в том, что не существует единственного способа определить релятивистскую массу и получить согласованные результаты. С релятивистской массой нужно обращаться очень осторожно, иначе вы получите странные понятия, такие как тангенциальная масса против радиальной массы. Как масса может иметь направление? Например, при расчете отклонения света, когда он проходит мимо такой большой массы, как Солнце, можно сказать, что этот свет имеет «релятивистскую массу», равную E/c ², а затем используйте формулу Ньютона, чтобы определить, как гравитация влияет на него. Это даст вам правильный ответ, если свет движется к Солнцу или от него, но даст неправильный ответ, если вы попытаетесь использовать его для света, движущегося сбоку от Солнца.
Ситуация становится еще хуже, когда мы переходим к общей теории относительности (как и следовало ожидать, учитывая приведенный выше пример). В общей теории относительности вообще не существует единственного последовательного способа определения массы. Во многих особых случаях существуют полезные версии массы, но разные для разных обстоятельств (масса АДМ для асимптотически плоского пространства-времени, масса Комрара для статического/стационарного пространства-времени и т. д.). Сейчас мы сосредоточимся на специальной теории относительности.
Учитывая, как легко концепция релятивистской массы может привести к путанице, некоторые физики (особенно физики элементарных частиц) отстаивают идею о том, что термин «масса» должен означать только «массу покоя».
Масса покоя является релятивистским инвариантом (по крайней мере, в специальной теории относительности), и в физике мы обычно ищем инвариантные качества как в некотором смысле «более глубокие», чем свойства, зависящие от наблюдателя. Поэтому имеет смысл сосредоточиться на этом и избежать всей этой путаницы. Таким образом, эти физики заключают, что так должен поступать каждый.
Но что такое масса покоя? Это немного сложно, потому что рассматриваемая таким образом масса — это не свойство объектов, а скорее свойство систем. Масса покоя — это масса системы в ее центре масс. Если система в целом движется, то ее общая кинетическая энергия не является частью ее массы покоя, а кинетическая энергия, обусловленная внутренним движением, является частью массы покоя. Это аналогично идее внутренней энергии в термодинамике, где общая кинетическая энергия системы в целом не является частью внутренней энергии, а «скрытая» внутренняя кинетическая энергия частиц, составляющих систему, является частью внутренней энергии. внутреннюю энергию.
Что не так с релятивистской массой?
Декларация о том, что мы должны изгнать термин «релятивистская масса», — вот где проявляется «политический» элемент этих дебатов. Каждый взгляд на значение массы имеет свои положительные и отрицательные аспекты, и утверждение, что любой из них является «единственным верным путем», является не научным или даже педагогическим выбором, а идеологическим выбором.
Идея о том, что «только масса покоя является массой», сама по себе подвержена недоразумениям и заблуждениям. Масса покоя является свойством системы, и то, что считается релятивистской массой внутри этой системы, будет казаться частью массы покоя, если вы находитесь вне ее. Например, масса покоя шарового скопления представляет собой сумму релятивистских масс вращающихся вокруг звезд внутри скопления. Точно так же масса покоя протона в сто раз больше массы покоя кварков, из которых он «сделан», потому что протоны имеют огромное количество энергии, запасенной в полях и в кинетической энергии этих кварков, т. е. их релятивистская масса . Таким образом, принимая позицию «масса означает массу покоя», мы обретаем независимость от наблюдателя для нашего определения массы, но обмениваем на нее другой вид универсальности.
Так, например, система, состоящая из двух масс, движущихся в одном и том же направлении, имеет другую массу покоя, чем система, состоящая из тех же двух масс, движущихся в противоположных направлениях (обратите внимание на сходство с тем, как механическая энергия и внутренняя энергия энергия зависит от того, как вы думаете о системе!):
Рисунок 1: Масса покоя системы, как правило, не является суммой или массами покоя частей системы

Таким образом, релятивистская масса сохраняет некоторые свойства массы, которые мы ожидаем: она описывает, насколько трудно ее изменить движение чего-либо и масса системы равна массе ее частей. Ни одна из этих особенностей не сохраняется при подходе «масса означает массу покоя».
Позвольте мне привести пример путаницы, с которой я столкнулся из-за идеи «масса = масса покоя»:
Несколько лет назад друг, интересующийся физикой, пришел ко мне с проектом «безреактивного привода». Он знал, что что-то не так, но не видел, что. Идея такова: возьмите длинную коробку с источником фотонов на одном конце и, скажем, фотоэлементом на другом. Теперь сделайте так, чтобы источник фотонов излучал импульс света или один фотон, если хотите. Свет имеет импульс влево, поэтому коробка сдвинется вправо:

Рис. 2. Где находится центр масс по мере распространения света?

Каким-то образом по мере распространения света коробка двигалась без какого-либо видимого взаимодействия с внешним миром.
Мы видим, что конец коробки с фотоэлементом теперь «более массивен», чем раньше, а другой конец «менее массивен», потому что движение энергии сдвинуло часть массы, оставив центр масс на том же месте. … но если у нас есть точка зрения «масса = масса покоя», трудно обосновать это, не зная, в какой форме находится энергия. Кроме того, пока свет движется, у него однозначно нет массы покоя, так как же он может воздействовать на центр масса?
Проблема в том, что свет имеет массу покоя, пока мы ограничиваем систему рамками. Но у него не будет массы покоя, если мы поместим границы только вокруг источника света и исключим коробку. Если «масса» всегда означает «массу покоя», то у нас здесь некоторая неразбериха… ее можно решить в представлении без релятивистской массы, но только имея дело со сложными и хитрыми определениями и высоким риском путаницы.
С другой стороны, коробка и свет, рассматриваемые с точки зрения релятивистской массы, намного проще… центр масс коробки никогда не перемещается, потому что, когда свет движется, он несет энергию, которая является частью «релятивистской массы» системы, и ситуация как раз как классический пример человека, идущего навстречу задней части лодки в механике.
В качестве дополнительной защиты идеи релятивистской массы рассмотрим, как обрабатывается длина. Остаток или правильная длина также неизменны, но мало кто выступает за использование термина «длина» только для обозначения правильной длины. Мы готовы признать, что разные кадры измеряют длину по-разному, потому что мы считаем, что длина — это то, что измеряется измерением! Если кто-то другой измеряет другую длину, то длина просто не является абсолютной вещью, которую мы думали. Таким же образом мы могли бы решить определить массу как вещь, которую мы «измеряем», глядя, например, на силу, необходимую для ускорения объекта. И это означает, что наблюдатель зависит почти так же, как и длина.
Когда E встречается с mc ² :
Чтобы увидеть, как разыгрывается битва определений, полезно взглянуть на, вероятно, самое известное и, следовательно, наиболее неправильно понятое уравнение в физике: E = mc ² .
Те, кто хочет использовать релятивистскую массу, захотят утверждать, что это утверждение описывает полную энергию системы, используя релятивистскую массу, чтобы показать это: для них E = mc ² означает E = м _отн c ² = γm ₀ c ^290.
С другой стороны, те, кто предпочитает массу массе покоя, скажут, что E = mc ² следует заменить «правильным» или «полным» выражением E ² = (mc 2 ) ² + (шт) ² (или в других обозначениях E ² = (m ₀ c ² ) ² + (шт) ² ). У Minutephysics, например, есть отличное видео, подтверждающее этот аргумент.
Но эти два уравнения математически идентичны, начиная с любого из них и выполняя некоторые алгебраические действия, мы получим другую форму. Следовательно, нет математического предпочтения одного перед другим, и каждый имеет свою ценность с точки зрения понимания физики.
E = mc ² ценен, потому что он подчеркивает идентичность между массой и энергией и, следовательно, тот факт, что увеличение содержания энергии в чем-то меняет то, как оно реагирует на силы. Например, частица, движущаяся с релятивистской скоростью в магнитном поле, имеет радиус кривизны, который зависит от ее «релятивистской массы», и отклонить движущийся объект труднее, потому что он фактически имеет большую массу. (По этой причине я в качестве компромисса обычно использую термин «эффективная масса», а не «релятивистская масса»).
Помнить об этой эквивалентности также полезно для понимания того, что, например, горячая чашка с водой имеет большую массу, чем холодная (хотя и ненамного), и что протон внутри ядра имеет другую массу покоя чем вне ядра. Это сложные идеи для понимания, если мы думаем о массе как о фиксированном свойстве объекта. И, конечно же, запись энергии в виде E = mc ² помогает нам понять выражение для кинетической энергии E 9.0147 K = (γ-1) M ₀ C ². ) — энергия в неподвижном состоянии (m ₀ c ² ) … что кажется довольно разумным описанием.
С другой стороны E ² = (m ₀ c ² ) ² + (pc) ² ценен тем, что подчеркивает, что импульс не зависит от наличия массы покоя, что помогает устранить путаницу, с которой сталкиваются учащиеся, когда узнают, что «безмассовые» фотоны обладают импульсом. Его также очень удобно использовать в ситуациях релятивистских столкновений. Наконец, это представление также можно использовать для представления идеи о том, что энергия объекта является временной составляющей четырехмерного импульса.
Этот 4-импульс, который Уилер назвал мом-энергией, имеет импульс в знакомых направлениях пространства, а также импульс во времени (что является энергией). Пространственно-временная длина 4-вектора — это энергия, которую мы можем видеть, сравнивая наше уравнение с пространственно-временным интервалом, записывая его как дающее энергию покоя: E ₀ ² = E ² – (cp) ² так же, как пространственно-временной интервал равен Δs ² = (ct) ² – x ² (различное расположение c обусловлено используемыми единицами измерения, а не различием в физике.)

, с метрикой Минковского

Мы привыкли к тому, что разные модели или подходы полезны в разных ситуациях. Можно было бы ожидать, что мы могли бы принять идею множественных моделей и здесь, но в попытке изгнания релятивистской массы есть определенный идеологический элемент, который иногда приближается к фанатизму. Это скорее похоже на исключение «центробежной силы» из преподавания физики. Центробежная сила — это иллюзорная сила, наблюдаемая во вращающейся системе координат. Поскольку это зависит от фрейма, это может привести к значительной путанице для студентов, и я вырос с часто повторяемым рефреном о том, что «центробежной силы не существует», звенящим в моих ушах. Однако вы по-прежнему найдете множество физиков, которые регулярно используют эту идею, так же как они говорят о силах Кориолиса и т. д. В правильных обстоятельствах эта идея весьма полезна. Кроме того, есть еще одна иллюзорная сила, которую мы вовсе не изгнали таким образом: гравитация! В общей теории относительности «сила» гравитации является иллюзорной силой точно так же, как и центробежная сила. Однако мы сохраняем эту концепцию, потому что она очень полезна.
В пропаганде осторожности при использовании релятивистской массы есть реальная заслуга, потому что она не очень хорошо переносится в такие области, как физика элементарных частиц или даже общая теория относительности. Но вы не должны позволять никому говорить вам, что релятивистская масса — это плохая концепция. Это просто концепция, которая полезна в одних обстоятельствах и бесполезна в других, как и любая другая физическая концепция.
Действовать осторожно.
Если вы используете массу покоя/релятивистскую массу:
Какие возражения/предостережения следует выдвигать относительно концепции релятивистской массы на разных уровнях?
Первый относится к гравитации… где тот факт, что масса является свойством системы, усложняет ситуацию. Быстро движущийся объект может иметь очень большую «релятивистскую массу», но он не превратится в черную дыру или что-то в этом роде. На свет действует гравитационное поле, но не так, как если бы он имел массу m = E/c ² . Тем не менее, гравитация двух объектов, находящихся на орбите, действительно отличается от той, которая была бы в состоянии покоя, а на свет воздействует гравитация и она создает ее. Так что это сложно… когда речь идет о гравитации, «релятивистская масса», скорее всего, направит нас по ложному пути.
Еще одна и более сложная проблема с релятивистской массой заключается в том, что она затемняет более глубокие идеи, перенося важность с «геометрии» на «объект». Например, рассмотрим аргумент: «Вы не можете достичь скорости света, потому что чем ближе объект (скажем, космический корабль) приближается к скорости света, тем более массивным становится корабль и тем труднее ему набрать скорость». Это не совсем неправильно… это совершенно последовательный аргумент, и то, что он говорит, верно. Однако он скрывает тот факт, что скорость света не просто недостижима по «практическим» причинам — здесь есть нечто более важное. Скорость света является пределом не потому, что ее невозможно достичь, а из-за сущностной структуры Вселенной, это универсальная максимальная скорость. Это и многое другое следует из того, что эта скорость есть абсолют для всех наблюдателей, а предел вплетен в природу причинности. Скорость света — это предел, потому что это не скорость, так же как «бесконечность» — это не число. Бесконечность — это не то, чего вы можете достичь, просто «добавляя больше», а скорость света — это не то, чего вы можете достичь, просто «двигаясь быстрее». Скорость света – это универсальная скорость, равная одной секунде в секунду. Для того, кто наблюдает за собой, это просто течение времени. Однако, если вы движетесь относительно меня, ваше время смешивается для меня с пространством. Чем быстрее вы движетесь, тем больше пространства смешивается. Когда вы достигаете скорости света, ваше время достигает точки, когда оно не может быть меньше, и ваше движение в пространстве «максимально». Это означает, что «масса увеличивается, потому что вы не можете достичь скорости света», а не вы не можете достичь скорости света, потому что масса увеличивается». Это более основная идея, чем просто прагматический предел, который идея увеличения массы имеет тенденцию давать студентам.
Если вы хотите избежать релятивистской массы:
Если вы решите отказаться от релятивистской массы, вы избежите описанных выше проблем, но добавите несколько новых.
Одна проблема заключается в том, что такой способ говорить о массе может заставить некоторых людей думать о массе как о чем-то отдельном от энергии… вы слышите, как люди говорят что-то вроде «масса преобразуется в энергию», что, как кто-то однажды заметил, похоже на высказывание « моя машина была переделана в автомобиль». В этом отношении есть аргументы как за, так и против релятивистской массы. Использование идеи релятивистской массы подчеркивает связь между понятиями массы и энергии, поскольку таким образом мы рассматриваем энергию как массу. С другой стороны, мы могли бы возразить против релятивистской массы, указав, что, поскольку «релятивистская масса» и энергия — это одно и то же, зачем использовать два слова? Используйте «массу» для того, для чего мы используем ее в нашем повседневном опыте («масса покоя»), и просто используйте «энергию» для другого. В этом есть смысл, но не всегда. Все сложно.
Если вы хотите избавиться от идеи релятивистской массы, вам также следует пояснить, что масса (ранее известная как масса покоя) является свойством систем, а не объектов. Масса системы, вообще говоря, не равна сумме ее частей. Кроме того, масса больше не связана с силой и ускорением — эта связь уже разорвана в специальной теории относительности, но разрыв будет более полным, если мы определим массу таким образом.
Общее предложение:
Физика является и должна быть мультикультурной страной, так же как Канада стремится быть мультикультурной страной, и я думаю, что применимы те же правила. Независимо от того, считаете ли вы идею релятивистской массы полезной или вредной, возможно, лучше признать, что культурное разнообразие может обогатить наше понимание, и нам не нужно, чтобы все придерживались одной точки зрения, чтобы работать вместе. И, может быть, если мы научим наших студентов тому, что эти разные точки зрения существуют, они тоже смогут усвоить этот урок. Мира, порядка и хорошей физики!
Теги: Современная физика
28.6 Релятивистская энергия — College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
Вычисление полной энергии релятивистского объекта.
Вычислите кинетическую энергию релятивистского объекта.
Опишите энергию покоя и объясните, как ее можно преобразовать в другие формы.
Объясните, почему массивные частицы не могут достичь C.
Рисунок 28.20 В Национальном эксперименте по сферическому тору (NSTX) есть термоядерный реактор, в котором изотопы водорода подвергаются синтезу с образованием гелия. В этом процессе относительно небольшая масса топлива преобразуется в большое количество энергии. (кредит: Принстонская лаборатория физики плазмы)
Токамак — это форма экспериментального термоядерного реактора, который может преобразовывать массу в энергию. Для этого требуется понимание релятивистской энергии. Ядерные реакторы являются доказательством сохранения релятивистской энергии.
Закон сохранения энергии — один из важнейших законов физики. Мало того, что энергия имеет много важных форм, каждая форма может быть преобразована в любую другую. Мы знаем, что в классическом понимании общее количество энергии в системе остается постоянным. Релятивистски энергия по-прежнему сохраняется при условии, что ее определение изменено, чтобы включить возможность превращения массы в энергию, как в реакциях, происходящих в ядерном реакторе. Релятивистская энергия намеренно определена таким образом, чтобы она сохранялась во всех инерциальных системах отсчета, как и в случае с релятивистским импульсом. Как следствие, мы узнаем, что несколько фундаментальных величин связаны способами, неизвестными в классической физике. Все эти соотношения проверяются экспериментом и имеют фундаментальные последствия. Измененное определение энергии содержит некоторые из наиболее фундаментальных и захватывающих новых открытий в природе, обнаруженных в новейшей истории.
Общая энергия и энергия покоя
Первый постулат относительности гласит, что законы физики одинаковы во всех инерциальных системах отсчета. Эйнштейн показал, что закон сохранения энергии верен релятивистски, если мы определяем энергию как включающую релятивистский фактор.
Общая энергия
Полная энергия EE определена как скорость массы относительно наблюдателя. Есть много аспектов полной энергии EE, которые мы обсудим — среди них то, как кинетическая и потенциальная энергии включаются в EE и как EE связана с релятивистским импульсом. Но сначала отметим, что в состоянии покоя полная энергия не равна нулю. Скорее, когда v=0v=0, мы имеем γ=1γ=1, и у объекта есть энергия покоя.
Энергия покоя
Энергия покоя
E0=mc2.E0=mc2.
28,44
Это правильная форма самого известного уравнения Эйнштейна, которое впервые показало, что энергия связана с массой покоящегося объекта. Например, если в объекте запасена энергия, его масса покоя увеличивается. Это также означает, что масса может быть разрушена для высвобождения энергии. Последствия этих первых двух уравнений относительно релятивистской энергии настолько широки, что они не были полностью осознаны в течение нескольких лет после того, как Эйнштейн опубликовал их в 1919 году. 07, и экспериментальное доказательство их правильности поначалу не было общепризнанным. Следует отметить, что Эйнштейн действительно понял и описал значения и следствия своей теории.
Пример 28,6
Расчет энергии покоя: Энергия покоя очень велика
Рассчитайте энергию покоя груза массой 1,00 г.
Стратегия
Один грамм — это небольшая масса — менее половины массы пенни. Мы можем умножить эту массу в единицах СИ на квадрат скорости света, чтобы найти эквивалентную энергию покоя.
Решение
Определите известное. m=1,00×10-3 кгm=1,00×10-3 кг; с=3,00×108 м/с=3,00×108 м/с
Определите неизвестное. E0E0
Выберите подходящее уравнение. E0=mc2E0=mc2
Подставьте известные значения в уравнение.
E0=mc2=(1,00×10-3кг)(3,00×108м/с)2=9,00×1013кг⋅м2/с2E0=mc2=(1,00×10-3кг)(3,00×108м/с)2=9,00×1013кг ⋅м2/с2
28,45
Преобразовать единицы.
Учитывая, что 1кг⋅м2/с2=1 Дж1кг⋅м2/с2=1 Дж, получаем, что энергия массы покоя равна
E0=9,00×1013 Дж.E0=9,00×1013 Дж.
28,46
Обсуждение
Это огромное количество энергии для массы в 1,00 г. Мы не замечаем эту энергию, потому что она вообще недоступна. Энергия покоя велика, потому что скорость света cc — большое число, а c2c2 — очень большое число, так что mc2mc2 огромно для любой макроскопической массы. Энергия массы покоя 9,00×1013J9,00×1013Дж для 1,00 г примерно в два раза превышает энергию, высвобожденную атомной бомбой, сброшенной на Хиросиму, и примерно в 10 000 раз превышает кинетическую энергию большого авианосца. Если будет найден способ преобразования энергии массы покоя в какую-либо другую форму (а все формы энергии могут быть преобразованы друг в друга), то при разрушении массы можно будет получить огромное количество энергии.
Сегодня хорошо известны практические применения преобразования массы в другую форму энергии , например, в ядерном оружии и атомных электростанциях. Но примеры существовали и тогда, когда Эйнштейн впервые предложил правильную форму релятивистской энергии, и он действительно описал некоторые из них. Ядерное излучение было обнаружено в предыдущем десятилетии, и оставалось загадкой, откуда берется его энергия. Объяснение заключалось в том, что в некоторых ядерных процессах небольшое количество массы разрушается, а энергия высвобождается и переносится ядерным излучением. Но количество уничтоженной массы настолько мало, что трудно обнаружить отсутствие чего-либо. Хотя Эйнштейн предположил, что это источник энергии в изучаемых в то время радиоактивных солях, прошло много лет, прежде чем было широко признано, что масса может быть преобразована и фактически обычно преобразуется в энергию. (См. рис. 28.21.)
Рисунок 28.21 Солнце (а) и паровая электростанция в Саскуэханне (б) преобразуют массу в энергию: Солнце — посредством ядерного синтеза, электрическая станция — посредством ядерного деления. (кредиты: (а) НАСА/Центр космических полетов имени Годдарда, Студия научной визуализации; (б) правительство США)
Из-за связи энергии покоя с массой мы теперь считаем массу формой энергии, а не чем-то отдельным. До работы Эйнштейна не было даже намека на это. Теперь известно, что такое преобразование является источником солнечной энергии, энергии ядерного распада и даже источником энергии, поддерживающей недра Земли горячими.
Сохраненная энергия и потенциальная энергия
Что происходит с энергией, хранящейся в покоящемся объекте, например, с энергией, переданной в батарею при ее зарядке, или с энергией, запасенной в сжатой пружине игрушечного пистолета? Вклад энергии становится частью полной энергии объекта и, таким образом, увеличивает его массу покоя. Вся запасенная и потенциальная энергия становится массой в системе. Почему мы обычно этого не замечаем? На самом деле, сохранение массы (что означает, что общая масса постоянна) было одним из великих законов, подтвержденных 19наука X века. Почему не было замечено, что это неправильно? Следующий пример поможет ответить на эти вопросы.
Пример 28,7
Расчет массы покоя: небольшое увеличение массы из-за подводимой энергии
Автомобильный аккумулятор рассчитан на то, чтобы обеспечить 600 ампер-часов (А·ч) (А·ч) заряда при 12,0 В. (a) Вычислить увеличение массы покоя такой батареи, когда она переходит от полностью разряженного состояния к полностью заряженному. б) На сколько процентов это увеличение, учитывая массу батареи 20,0 кг?
Стратегия
В части (а) мы сначала должны найти энергию, запасенную в батарее, которая равняется тому, что батарея может дать в виде электрической потенциальной энергии. Поскольку PEelec=qVPEelec=qV, мы должны рассчитать заряд qq в 600A·h600A·ч, который является произведением тока II на время tt. Затем мы умножаем результат на 12,0 В. Затем мы можем рассчитать увеличение массы батареи, используя ΔE=PEelec=(Δm)c2 ΔE=PEelec=(Δm)c2. Часть (b) представляет собой простое соотношение, переведенное в проценты.
Решение для (а)
Определите известные. I⋅t=600 А⋅чI⋅t=600 А⋅ч; В=12,0ВВ=12,0В; с=3,00×108 м/с=3,00×108 м/с
Определите неизвестное. ΔmΔm
Выберите подходящее уравнение. PEelec=(Δm)c2PEelec=(Δm)c2
Переформулируйте уравнение, чтобы найти неизвестное. Δm=PEelecc2Δm=PEelecc2
Подставьте известные значения в уравнение.
Δm=PEelecc2=qVc2=(It)Vc2=(600 А⋅ч)(12,0 В)(3,00×108)2.Δm=PEelecc2=qVc2=(It)Vc2=(600 А⋅ч)(12,0 В) (3,00×108)2.
28,47
Запишите ампер A в кулонах в секунду (Кл/с) и переведите часы в секунды.
Δm=(600 Кл/с⋅ч4600 с1 ч(12,0 Дж/Кл)(3,00×108 м/с)2=(2,16×106 Кл)(12,0 Дж/Кл)(3,00×108 м/с)2Δm= (600 Кл/с⋅ч4600 с1 ч(12,0 Дж/Кл)(3,00×108 м/сек)2=(2,16×106 Кл)(12,0 Дж/Кл)(3,00×108 м/сек)2
28,48
Используя преобразование 1кг⋅м2/с2=1Дж1кг⋅м2/с2=1Дж, можно записать массу как
Δm=2,88×10-10 кг.Δm=2,88×10-10 кг
Решение для (б)
Определите известное. Δm=2,88×10-10 кг; Δm=2,88×10-10 кг; m=20,0 кгm=20,0 кг
Определите неизвестное. % изменения
Выберите подходящее уравнение. % увеличение=Δмм×100%% увеличение=Δмм×100%
Подставьте известные значения в уравнение.
% увеличение=Δмм×100%=2,88×10-10 кг20,0 кг×100%=1,44×10-9%.% увеличение=Δмм×100%=2,88×10-10 кг20,0 кг×100%= 1,44×10-9%.
28.49
Обсуждение
Как фактическое увеличение массы, так и увеличение в процентах очень мало, так как энергия делится на c2c2, очень большое число. Нам нужно было бы измерить массу батареи с точностью до одной миллиардной доли процента, или 1 части на 10111011, чтобы заметить это увеличение. Неудивительно, что изменение массы не так просто наблюдать. На самом деле это изменение массы настолько мало, что мы можем задаться вопросом, как вы можете проверить, что оно реально. Ответ можно найти в ядерных процессах, в которых процент разрушенной массы достаточно велик, чтобы его можно было измерить. Масса топлива ядерного реактора, например, значительно меньше, когда его энергия была использована. В этом случае запасенная энергия высвобождается (превращается в основном в тепло и электричество), а масса покоя уменьшается. Это также имеет место, когда вы используете энергию, хранящуюся в батарее, за исключением того, что запасенная энергия намного больше в ядерных процессах, что делает изменение массы измеримым как на практике, так и в теории.
Кинетическая энергия и максимальный предел скорости
Кинетическая энергия – это энергия движения. Классически кинетическая энергия имеет известное выражение 12mv212mv2. Релятивистское выражение для кинетической энергии получается из теоремы о работе-энергии. Эта теорема утверждает, что чистая работа системы переходит в кинетическую энергию. Если наша система запускается из состояния покоя, то теорема о работе-энергии равна
Wnet=KE.Wnet=KE.
28,50
Релятивистски в состоянии покоя мы имеем энергию покоя E0=mc2E0=mc2. Работа увеличивает ее до полной энергии E=γmc2E=γmc2. Таким образом,
Wnet=E-E0=γmc2-mc2=γ-1mc2.Wnet=E-E0=γmc2-mc2=γ-1mc2.
28,51
Релятивистски имеем Wnet=KErelWnet=KErel.
Релятивистская кинетическая энергия
Релятивистская кинетическая энергия
KErel=γ-1mc2.KErel=γ-1mc2.
28,52
В неподвижном состоянии имеем v=0v=0 и
γ=11−v2c2=1,γ=11−v2c2=1,
28,53
, так что KErel=0KErel=0 в состоянии покоя, как и ожидалось. Но выражение для релятивистской кинетической энергии (такой как полная энергия и энергия покоя) мало похоже на классическое 12mv212mv2. Чтобы показать, что классическое выражение для кинетической энергии получается при малых скоростях, заметим, что биномиальное разложение для γγ при малых скоростях дает
γ=1+12v2c2.γ=1+12v2c2.
28,54
Биномиальное разложение — это способ выражения алгебраической величины в виде суммы бесконечного ряда членов. В некоторых случаях, как здесь в пределе малой скорости, большинство членов очень малы. Таким образом, полученное здесь выражение для γγ не является точным, но является очень точным приближением. Таким образом, при малых скоростях
γ−1=12v2c2.γ−1=12v2c2.
28,55
Ввод этого в выражение для релятивистской кинетической энергии дает
KErel=12v2c2mc2=12mv2=KEclass.KErel=12v2c2mc2=12mv2=KEclass.
28,56
Таким образом, фактически релятивистская кинетическая энергия становится такой же, как классическая кинетическая энергия, когда v<
Еще интереснее исследовать, что происходит с кинетической энергией, когда скорость объекта приближается к скорости света. Мы знаем, что γγ становится бесконечным, когда vv приближается к cc, так что KE _rel также становится бесконечным, когда скорость приближается к скорости света. (См. рис. 28.22.) Чтобы разогнать массу до скорости света, требуется бесконечное количество работы (и, следовательно, бесконечное количество подводимой энергии).
Скорость света
Ни один объект с массой не может достичь скорости света.
Таким образом, скорость света является предельной скоростью для любой частицы, имеющей массу. Все это согласуется с тем фактом, что скорость меньше cc всегда добавляется к скорости меньше cc. Как релятивистская форма кинетической энергии, так и предельное ограничение скорости, равное cc, были подробно подтверждены в многочисленных экспериментах. Независимо от того, сколько энергии затрачено на ускорение массы, ее скорость может только приближаться, а не достигать скорости света.
Рисунок 28.22 Этот график зависимости KErelKErel от скорости показывает, как кинетическая энергия приближается к бесконечности, когда скорость приближается к скорости света. Таким образом, объект, имеющий массу, не может достичь скорости света. Также показан KEclassKEclass, классическая кинетическая энергия, которая аналогична релятивистской кинетической энергии при низких скоростях. Обратите внимание, что для достижения высоких скоростей требуется гораздо больше энергии, чем предсказывалось классически.
Пример 28,8
Сравнение кинетической энергии: релятивистская энергия с классической кинетической энергией
Скорость электрона v=0,990cv=0,990c. а) Рассчитайте кинетическую энергию электрона в МэВ. (b) Сравните это с классическим значением кинетической энергии при этой скорости. (Масса электрона 9,11×10−31 кг9,11×10−31 кг.)
Стратегия
Выражение для релятивистской кинетической энергии всегда верно, но для (а) его необходимо использовать, поскольку скорость равна высокорелятивистский (близкий к cc). Сначала вычислим релятивистский фактор γγ, а затем используем его для определения релятивистской кинетической энергии. Для (b) мы рассчитаем классическую кинетическую энергию (которая была бы близка к релятивистскому значению, если бы vv было меньше нескольких процентов от cc) и увидим, что это не одно и то же.
Решение для (а)
Определите известные. v=0,990cv=0,990c; m=9,11×10-31кгm=9,11×10-31кг
Определите неизвестное. KErelKErel
Выберите подходящее уравнение. KErel=γ−1mc2KErel=γ−1mc2
Подставьте известные значения в уравнение.
Сначала рассчитайте γγ. Мы будем нести лишние цифры, потому что это промежуточный расчет.
γ=11−v2c2=11−(0,990c)2c2=11−(0,990)2=7,0888γ=11−v2c2=11−(0,990c)2c2=11−(0,990)2=7,0888
28,57
Далее мы используем это значение для расчета кинетической энергии.
KEотн=(γ−1)mc2=(7,0888−1)(9,11×10–31 кг)(3,00×108 м/с)2=4,99×10–13 JKEотн=(γ−1)mc2=(7,0888− 1)(9,11×10–31 кг)(3,00×108 м/с)2=4,99×10–13 Дж
28,58
Преобразовать единицы.
KErel=(4,99×10–13 Дж)1 МэВ1,60×10–13 J=3,12 МэВKErel=(4,99×10–13 Дж)1 МэВ1,60×10–13 J=3,12 МэВ
28,59
Решение для (b)
Список известных. v=0,990cv=0,990с; m=9,11×10-31кгm=9,11×10-31кг
Список неизвестного. KEклассKEкласс
Выберите подходящее уравнение. KEclass=12mv2KEclass=12mv2
Подставьте известные значения в уравнение.
KEclass=12mv2=12(9,00×10–31 кг)(0,990)2(3,00×108 м/с)2=4,02×10–14 JKEclass=12mv2=12(9,00×10–31 кг)(0,990)2 (3,00×108 м/с)2=4,02×10–14 Дж
28,60
Преобразовать единицы.
KEclass=4,02×10–14 Дж1 МэВ1,60×10–13 J=0,251 МэВKEclass=4,02×10–14 Дж1 МэВ1,60×10–13 J=0,251 МэВ
28,61
Обсуждение
Как и следовало ожидать, поскольку скорость составляет 99,0% скорости света, классическая кинетическая энергия значительно отличается от правильного релятивистского значения. Отметим также, что классическое значение намного меньше релятивистского. На самом деле здесь KErel/KEclass=12.4KErel/KEclass=12.4. Это некоторое указание на то, как трудно заставить массу двигаться со скоростью, близкой к скорости света. Требуется гораздо больше энергии, чем предсказывалось классически. Некоторые люди интерпретируют эту дополнительную энергию как увеличение массы системы, но, как обсуждалось в «Релятивистском импульсе», это нельзя проверить однозначно. Не вызывает сомнений то, что требуется постоянно возрастающее количество энергии, чтобы приблизить скорость массы к скорости света. Энергия в 3 МэВ очень мала для электрона и может быть достигнута с помощью современных ускорителей частиц. SLAC, например, может ускорять электроны более чем до 50×109эВ=50 000 МэВ50×109 эВ=50 000 МэВ.
Есть ли смысл приближать vv к c чем 99,0% или 99,9%? Ответ положительный. Делая это, мы многому учимся. Энергия, которая переходит в высокоскоростную массу, может быть преобразована в любую другую форму, в том числе в совершенно новые массы. (См. рис. 28.23.) Большая часть того, что мы знаем о субструктуре материи и наборе экзотических короткоживущих частиц в природе, была получена таким образом. Частицы ускоряются до чрезвычайно релятивистских энергий и заставляют сталкиваться с другими частицами, создавая совершенно новые виды частиц. Паттерны характеристик этих ранее неизвестных частиц намекают на основную субструктуру всей материи. Эти частицы и некоторые их характеристики будут рассмотрены в разделе «Физика частиц».
Рисунок 28.23 Национальная ускорительная лаборатория Ферми недалеко от Батавии, штат Иллинойс, представляла собой коллайдер субатомных частиц, который ускорял протоны и антипротоны до энергии до 1 Тэв (триллион электронвольт). Круглые пруды возле колец были построены для отвода отработанного тепла. Этот ускоритель был остановлен в сентябре 2011 года. (Фото: Фермилаб, Рейдар Хан)
Релятивистская энергия и импульс
Классически мы знаем, что кинетическая энергия и импульс связаны друг с другом, поскольку
KEclass=p22m=(mv)22m=12mv2.KEclass=p22m=(mv)22m=12mv2.
28,62
Релятивистски мы можем получить связь между энергией и импульсом, алгебраически манипулируя их определениями. Это дает
E2=(pc)2+(mc2)2,E2=(pc)2+(mc2)2,
28,63
, где EE — релятивистская полная энергия, а pp — релятивистский импульс. Эта связь между релятивистской энергией и релятивистским импульсом более сложна, чем классическая, но мы можем получить некоторые интересные новые идеи, исследуя ее. Во-первых, полная энергия связана с импульсом и массой покоя. В состоянии покоя импульс равен нулю, и уравнение дает полную энергию как энергию покоя mc2mc2 (так что это уравнение согласуется с приведенным выше обсуждением энергии покоя). Однако по мере ускорения массы ее импульс pp увеличивается, что увеличивает общую энергию. При достаточно высоких скоростях член энергии покоя (mc2)2(mc2)2 становится пренебрежимо малым по сравнению с членом импульса (пк)2(пк)2; таким образом, E=pcE=pc при чрезвычайно релятивистских скоростях.
Если мы считаем, что импульс pp отличается от массы, мы можем определить следствия уравнения E2=(pc)2+(mc2)2,E2=(pc)2+(mc2)2 для частицы, имеющей нет массы. Если в этом уравнении принять mm за ноль, то E=pcE=pc, или p=E/cp=E/c. Этим импульсом обладают безмассовые частицы. В природе встречается несколько безмассовых частиц, в том числе фотоны (это кванты электромагнитного излучения). Другое следствие состоит в том, что безмассовая частица должна двигаться со скоростью cc и только со скоростью cc. Хотя рассмотрение взаимосвязи в уравнении E2=(pc)2+(mc2)2,E2=(pc)2+(mc2)2 выходит за рамки этого текста, мы можем видеть, что связь имеет важные следствия в специальной теории относительности.
Стратегии решения проблем относительности
Изучите ситуацию, чтобы определить, что необходимо использовать относительность . Релятивистские эффекты связаны с γ=11−v2c2γ=11−v2c2, количественным релятивистским фактором. Если γγ очень близко к 1, то релятивистские эффекты малы и очень мало отличаются от обычно более простых классических расчетов.
Точно определите, что нужно определить в задаче (идентифицируйте неизвестные).
Составьте список того, что дано или может быть выведено из поставленной задачи (укажите известное). В частности, обратите внимание на информацию об относительной скорости vv.
Перед выполнением каких-либо расчетов убедитесь, что вы понимаете концептуальные аспекты задачи. Решите, например, какой наблюдатель увидит увеличение времени или сокращение длины, прежде чем подставлять в уравнения. Если вы подумали о том, кто что видит, кто движется вместе с наблюдаемым событием, кто видит правильное время и т. д., вам будет гораздо легче определить, разумен ли ваш расчет.
Определите основной тип расчета, который необходимо выполнить для нахождения указанных выше неизвестных. Вы найдете краткое содержание раздела полезным для определения того, задействовано ли сокращение длины, релятивистская кинетическая энергия или какое-либо другое понятие.
Не округлять при вычислении. Как отмечено в тексте, вы должны часто выполнять вычисления со многими цифрами, чтобы увидеть желаемый эффект.
No related posts.

Релятивизм | Понятия и категории

РЕЛЯТИВИСТСКИЙ — Что такое РЕЛЯТИВИСТСКИЙ?

Релятивистская кинематика — материалы для подготовки к ЕГЭ по Физике

Одновременность событий

Относительность одновременности

Относительность промежутков времени

Относительность расстояний

Преобразования Лоренца

Релятивистский закон сложения скоростей

Релятивистский — понятие и значение

Часть речи

Словоформы

Синонимы wiki

Цифровое произношение

См. также

Релятивистская механика

Постулаты релятивистской механики

Основные положения релятивистской кинематики

Урок 21. релятивистские эффекты — Физика — 11 класс

относительность | Определение, уравнения и факты

Прочтите краткий обзор этой темы

Космология до теории относительности

Механическая вселенная

Релятивистская энергия | Физика

Цели обучения

Полная энергия и энергия покоя

Полная энергия

Энергия покоя

Пример 1. Расчет энергии покоя: Энергия покоя очень велика

Стратегия

Обсуждение

Накопленная энергия и потенциальная энергия

Пример 2. Расчет массы покоя: небольшое увеличение массы из-за подводимой энергии

Стратегия

Решение для Части 1

Решение для Части 2

Обсуждение

Релятивистская кинетическая энергия.

Скорость света

Пример 3. Сравнение кинетической энергии: релятивистская энергия с классической кинетической энергией

Стратегия

Решение для Части 1

Обсуждение

Стратегии решения проблем относительности

Проверьте свое понимание

Концептуальные вопросы

Задачи и упражнения

Избранные решения задач и упражнений

8 способов увидеть теорию относительности Эйнштейна в реальной жизни

Электромагниты

GPS-навигация

Желтый цвет золота

Стойкость золота к коррозии

Жидкая ртуть

Ваш старый телевизор

Свет

Дополнительные ресурсы

Релятивистская масса

История до сих пор: краткий обзор

Ньютона Пересмотренные законы

Законы сохранения

Сохранение импульса на бильярдном столе

Симметричное столкновение космического корабля

Насколько он симметричен?

Эйнштейн спасает закон сохранения импульса

Реальная масса

…Или?

Сохранение массы и энергии: кинетическая энергия и масса для очень быстрых Частицы

Кинетическая энергия и масса медленных частиц

Кинетическая энергия и масса частиц произвольной скорости

Обозначения:

Релятивистская масса или масса покоя? | Статьи

28.6 Релятивистская энергия — College Physics 2e

Цели обучения

Общая энергия и энергия покоя

Общая энергия

Энергия покоя

Пример 28,6

Расчет энергии покоя: Энергия покоя очень велика

Стратегия