Теория хаоса — Психологос
Введение в теорию хаоса
Что такое теория хаоса?
Фракталы создаются благодаря игре хаоса.
Теория хаоса это учение о постоянно изменяющихся сложных системах, основанное на математических концепциях, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему (реку́рсия — процесс повторения элементов самоподобным образом).
Неправильные представления о теории хаоса
Широкая общественность обратила внимание на теорию хаоса благодаря таким фильмам, как «Парк юрского периода», и благодаря им же, постоянно увеличивается опасение теории хаоса со стороны общества. Однако, как и в отношении любой вещи, освещаемой средствами массовой информации, в отношении теории хаоса возникло много неправильных представлений.
Фильм «Теория хаоса и антихаоса»
Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса — это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.
Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.
Это правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы — наследственной непредсказуемости системы — а на унаследованном ей порядке — общем в поведении похожих систем.
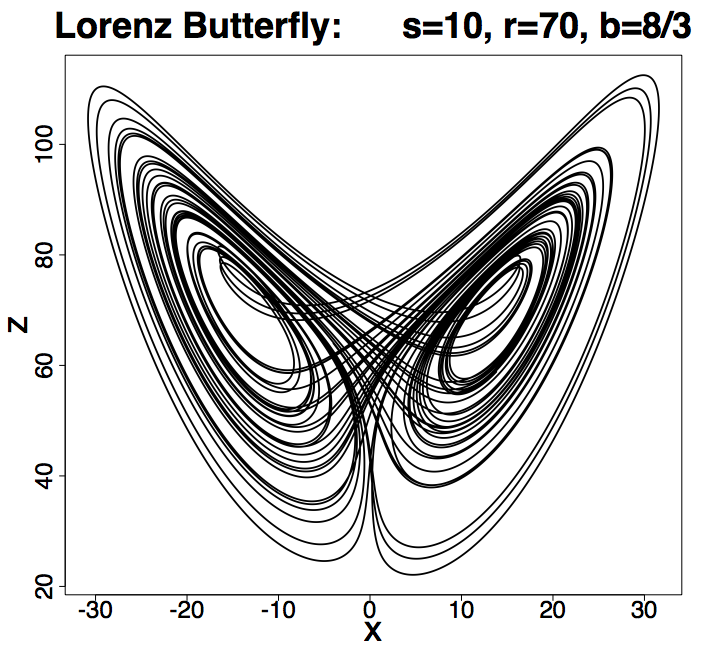
Таким образом, было бы неправильным сказать, что теория хаоса о беспорядке. Чтобы пояснить это на примере, возьмем аттрактор Лоренца. Он основан на трех дифференциальных уравнениях, трех константах и трех начальных условиях.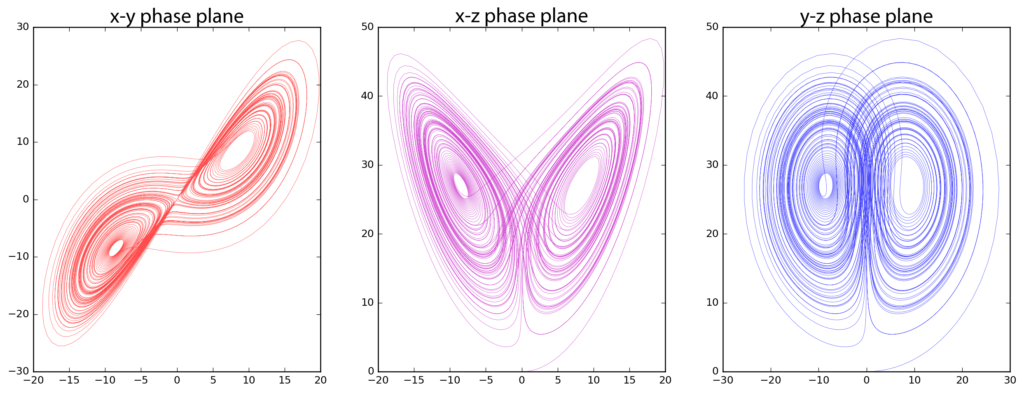
Теория хаоса о беспорядке
Аттрактор Лоренца как диаграмма хаотической системы. Эти два графика демонстрируют чувствительную зависимость от первоначальных условий в пределах занятого аттрактором региона.
Аттрактор представляет поведение газа в любое заданное время, и его состояние в определенный момент зависит от его состояния в моменты времени, предшествовавшие данному. Если исходные данные изменить даже на очень маленькие величины, скажем, эти величины малы настолько, что соизмеримы с вкладом отдельных атомов в число Авогадро (что является очень маленьким числом по сравнению со значениями порядка 1024), проверка состояния аттрактора покажет абсолютно другие числа. Это происходит потому, что маленькие различия увеличиваются в результате рекурсии.
Однако, несмотря на это, график аттрактора будет выглядеть достаточно похоже. Обе системы будут иметь абсолютно разные значения в любой заданный момент времени, но график аттрактора останется тем же самым, т.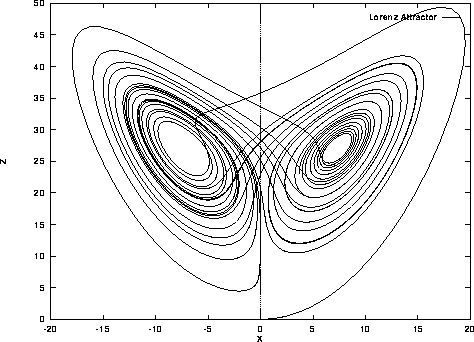
Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы — в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах.
Применение теории хаоса в реальном мире
Фрактальный папоротник, созданный благодаря игре хаоса. Природные формы (папоротники, облака, горы и т. д.) могут быть воссозданы через систему повторяющихся функций.
При появлении новых теорий, все хотят узнать что же в них хорошего. Итак что хорошего в теории хаоса? Первое и самое важное — теория хаоса — это теория. А значит, что большая ее часть используется больше как научная основа, нежели как непосредственно применимое знание.

Однако, согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни.
Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий до аритмических сердцебиений.
В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов в отличие от точных соотношений; процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.
Фракталы находятся везде, наиболее заметны в графических программах как например очень успешная серия продуктов Fractal Design Painter. Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.
Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
И, конечно, теория хаоса дает людям удивительно интересный способ того, как приобрести интерес к математике, одной из наиболее мало-популярной области познания на сегодняшний день.
Теория хаоса. Идеи, принципы, история
Однажды зимой 1961 года Эдвард Лоренц, метеоролог из Массачусетского технологического института проводил на громоздком и неуклюжем институтском ламповом компьютере простые симуляции погоды с помощью программы, которую сам написал. Он хотел повторить одну конкретную симуляцию, но не стал начинать с нуля — что всегда занимало много времени, — а взял исходные данные с распечатки предыдущего прогона. Он отошел налить себе чашку кофе, оставив компьютер работать, и вернулся, ожидая, что получит на выходе точное повторение предыдущего результата. К удивлению Лоренца, результат повторного прогона имел мало общего с результатом предыдущего.
Он хотел повторить одну конкретную симуляцию, но не стал начинать с нуля — что всегда занимало много времени, — а взял исходные данные с распечатки предыдущего прогона. Он отошел налить себе чашку кофе, оставив компьютер работать, и вернулся, ожидая, что получит на выходе точное повторение предыдущего результата. К удивлению Лоренца, результат повторного прогона имел мало общего с результатом предыдущего.
Теория хаоса – это наука о сложных нелинейных динамических системах. Отцом теории хаоса считается американский метеоролог Эдвард Лоренц
Сперва Лоренц подумал, что в компьютере перегорела одна из ламп, но вскоре догадался, что все не так просто. Исходные данные, которые он ввел, компьютер округлял с шести знаков после запятой до трех — на распечатке, но не в памяти. Ученый предполагал, что столь малое отклонение — примерно одна тысячная — едва ли окажет существенное влияние на результат. Но именно это и произошло. Едва заметное различие в начальных условиях привело к огромным различиям в результатах.
Научные модели
Чтоб как-то совладать со сложностью природных явлений — к примеру, климата, — ученые создают модели — упрощенные аналоги реальных явлений, позволяющие обнаружить и математически описать те или иные закономерности. Принято считать, что поведение моделей детерминировано: будущее состояние модели может быть полностью выведено из ее нынешнего состояния на основе математических закономерностей. Этот процесс может проходить через множество итераций — повторений, каждое из которых будет использовать результаты предыдущей итерации как исходные данные, позволяя делать все более и более долгосрочные прогнозы.
Именно таким методом пользовался Лоренц в 1961 году. И всего через несколько итераций программа выдала два совершенно разных результата на основе одних и тех же исходных данных, поставив под сомнение всю методологию. Модель, очевидно, повела себя непредсказуемо и произвела случайный результат: она продемонстрировала — хотя такой терминологии тогда еще не существовало — хаотическое поведение.
Чайки и бабочки
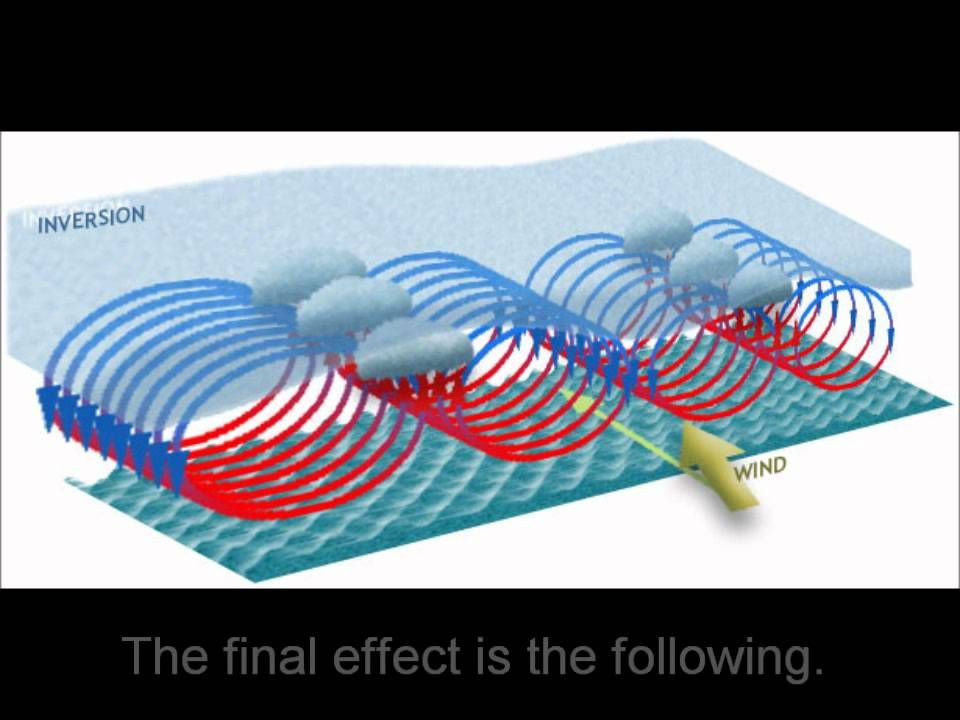
Почему симуляция Лоренца повела себя хаотически? Уравнения, используемые в предсказании погоды, описывают изменение некоторых существенных параметров, таких как температура, влажность, скорость и направление ветра. Важная особенность всех этих параметров в их взаимозависимости: например, уровень влажности зависит от температуры, а температура, в свою очередь, — от влажности.
В математических терминах это означает, что переменные являются функциями самих себя, и отношения между ними описываются нелинейными уравнениями, то есть на графике эти уравнения невозможно представить в виде прямой.
Одно из важнейших свойств системы нелинейных уравнений — чувствительность к начальным условиям, которая так удивила Лоренца в 1961 году. Позже он доказал, что эта чувствительность не зависит от сложности, поскольку проявляется и в более простых моделях (например, конвекции), которые описываются всего тремя нелинейными уравнениями. В 1963 году один из коллег метеоролога заметил, что если идеи Лоренца верны, то «чайка одним взмахом крыла может изменить погоду во всем мире».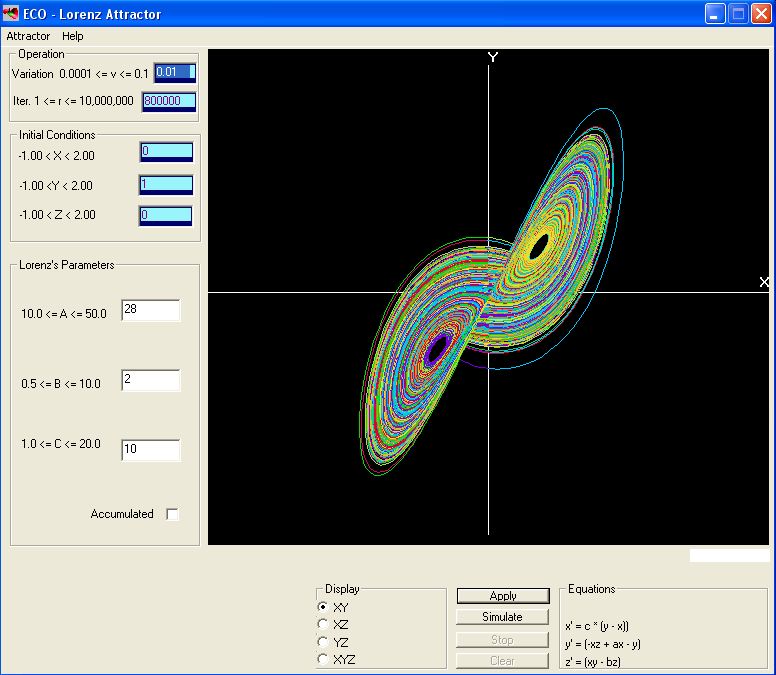 К 1972 году живое существо, способное нарушить баланс в атмосфере, стало еще меньше — вышедшая в этом году статья Лоренца называлась «Может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?». Так появился «эффект бабочки».
К 1972 году живое существо, способное нарушить баланс в атмосфере, стало еще меньше — вышедшая в этом году статья Лоренца называлась «Может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?». Так появился «эффект бабочки».
Порядок из беспорядка
«Оказывается, за фасадом порядка может скрываться пугающий хаос, — заметил американский ученый и писатель Дуглас Хофштадтер в 1985 году, — а внутри хаоса все равно скрывается пугающий порядок». Хаотические системы непредсказуемы, но это не значит, что их нельзя описать. Они вовсе не беспорядочны в обыденном, бытовом смысле. Уже в 1963 году простая модель конвекции, предложенная Лоренцом, показала поразительную упорядоченность: ее графическим выражением оказался дивной красоты абстрактный рисунок, напоминающий крылья бабочки, линии которого никогда не повторяются и не пересекаются. «Аттрактор Лоренца», как позже назвали изображение, стал первой из многочисленных топологических моделей хаотических систем, в которых плоскости складывались и растягивались, воспроизводя поведение и траекторию нелинейных систем. В 1970 году Бенуа Мандельброт и его коллеги разработали новую — фрактальную — геометрию, в которой появление порядка из хаоса демонстрируется нерегулярными фигурами, имеющими свойство самоподобия — их нерегулярность повторяется независимо от масштаба.
В 1970 году Бенуа Мандельброт и его коллеги разработали новую — фрактальную — геометрию, в которой появление порядка из хаоса демонстрируется нерегулярными фигурами, имеющими свойство самоподобия — их нерегулярность повторяется независимо от масштаба.
«Если даже в наших часах больше нет механизма, так с чего ему быть в нашем мире?» Иэн Стюарт, британский математик, 1989
Лоренц заключил, что долгосрочное прогнозирование погоды может быть в принципе невозможно, но этим выводы из теории хаотического поведения систем отнюдь не ограничиваются. Сложная система взаимозависимых факторов, определяющая климат, не уникальна — большинство и физических, и биологических систем имеют такой же характер, они описываются нелинейными уравнениями, и, следовательно, их модели будут неизбежно демонстрировать хаотическое поведение. Теория хаоса распространилась на множество научных дисциплин, связанных лишь присущей предметам их изучения беспорядочностью: турбулентность в динамике жидкостей, флуктуации в динамике популяций, циклы заболеваний в эпидемиологии, фибрилляции сердца в физиологии человека, движение планет и звезд в астрономии, потоки машин в городском трафике. С философской точки зрения способность хаотических с виду систем проявлять почти гипнотическую и завораживающе прекрасную упорядоченность позволяет нам надеяться, что Вселенная все-таки познаваема, и смириться с ее почти неприличной беспорядочностью.
С философской точки зрения способность хаотических с виду систем проявлять почти гипнотическую и завораживающе прекрасную упорядоченность позволяет нам надеяться, что Вселенная все-таки познаваема, и смириться с ее почти неприличной беспорядочностью.
Монтировкой теории хаоса по механизму ньютоновских «часов»
Еще в 1960 году большинство ученых, в том числе и Эдвард Лоренц, посчитали бы, что незначительное отклонение в исходных данных не имеет большого значения. До появления теории хаоса предполагалось, что мир в целом работает согласно механистической, детерминистской модели, которую тремя веками раньше предложил Ньютон (словно безмерно сложный часовой механизм). С такой точки зрения природные явления, в частности погоду, сложно предсказать просто потому, что они сами по себе исключительно сложны; но в принципе такое предсказание возможно, если удастся полностью понять все участвующие в формировании явления физические процессы и получить доступ ко всем необходимым данным. И надежность прогнозов, в том числе и метеорологических, зависит исключительно от качества исходных данных. Теория хаоса полностью опровергла это предположение.
Теория хаоса полностью опровергла это предположение.
Поиски смысла в беспорядке
Понятие «эффект бабочки» применяется, как правило, в естественных науках, а обозначается им особое свойство некоторых хаотичных систем, согласно которому, даже небольшое воздействие на систему может иметь самые непредсказуемые и крупные последствия в каком-то другом месте и в другой момент времени
Термин «эффект бабочки» быстро приобрел широкую популярность, но его истинное значение часто понимают неправильно. Обычно, говоря об «эффекте бабочки», имеют в виду, что зачастую причиной важных событий становятся мелочи, но на самом деле понятие это несколько шире. Взмах крыла бабочки становится причиной торнадо только в ограниченном смысле: торнадо могло бы и не возникнуть, если бы бабочка не взмахнула крылом, но на его появление так или иначе влияют миллионы, если не миллиарды, других факторов. Благодаря «эффекту бабочки» удалось оценить, насколько пугающе чувствительна система в целом даже к самым незначительным происходящим внутри нее событиям.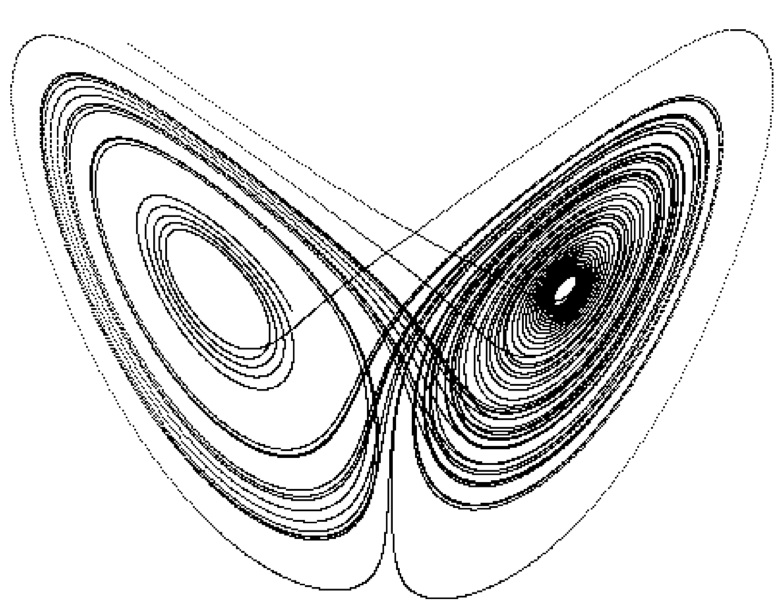 А из этого следует, что определить все причины того или иного события в системе практически невозможно. Если даже совсем незначительные события, в том числе и те, о которых мы в принципе не можем ничего знать, способны вызвать изменения всей системы, вполне вероятно, что полностью детерминированная система окажется при этом совершенно непредсказуемой.
А из этого следует, что определить все причины того или иного события в системе практически невозможно. Если даже совсем незначительные события, в том числе и те, о которых мы в принципе не можем ничего знать, способны вызвать изменения всей системы, вполне вероятно, что полностью детерминированная система окажется при этом совершенно непредсказуемой.
Поделиться ссылкой
Теория Хаоса. Когда настоящее определяет будущее… | Лутфи Рамадан | Интуиция
Наука
Когда настоящее определяет будущее, но приблизительное настоящее не определяет будущее приблизительно
Изображение Герда Альтманна на Pixabay , что означает, что конкретное начальное условие всегда развивается одним и тем же образом. Теория хаоса утверждает, что небольшое изменение начальных условий может привести к совершенно другому поведению. Это также известно как эффект бабочки , введенный Эдвардом Лоренцем из идеи, что простое взмах крыльев бабочки может вызвать ураган через несколько недель.
Эдвард Лоренц был математиком и метеорологом, который объединил две дисциплины для создания теории хаоса. В 1950-х годах Эдвард Лоренц искал способ прогнозировать погоду. В эксперименте по моделированию прогноза погоды он устанавливает начальные условия равными 0,506 вместо 0,506127. В результате получился другой прогноз. Из этого он сделал вывод, что погода должна измениться в мгновение ока. Небольшое изменение начальных условий имеет огромные долгосрочные последствия. Это показывает, что даже детальное моделирование атмосферы не может дать точных долгосрочных прогнозов погоды, потому что мы никогда не знаем начальных условий достаточно точно, чтобы точно предсказать погоду после определенного момента времени. Этой крошечной десятичной разницы достаточно, чтобы в долгосрочной перспективе давать крайне неточные прогнозы.
Условия возникновения хаоса
Существуют три обязательных математических свойства для классификации системы как хаотической:
- Чувствительность к начальным условиям
- Топологическое перемешивание
- Плотность периодических орбит
9000 Чувствительность к начальным условиям известный как эффект бабочки.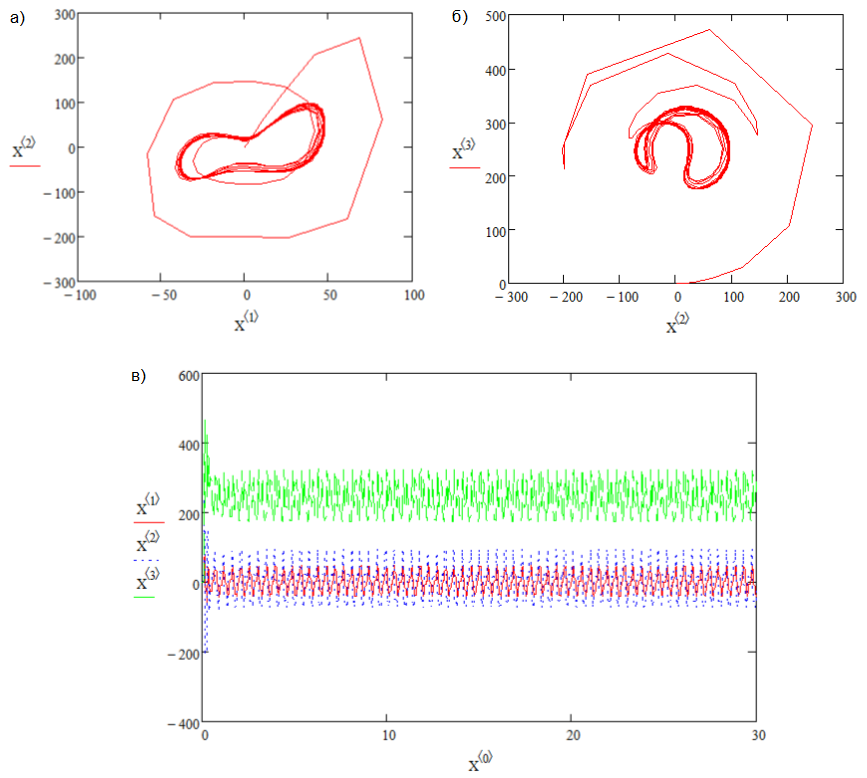 Эдвард Лоренц разработал упрощенную математическую модель атмосферной конвекции. Модель представляет собой систему трех обыкновенных дифференциальных уравнений, известную как Уравнения Лоренца :
Эдвард Лоренц разработал упрощенную математическую модель атмосферной конвекции. Модель представляет собой систему трех обыкновенных дифференциальных уравнений, известную как Уравнения Лоренца :
With:
- x как скорость конвекции
- y как горизонтальное изменение температуры
- z как вертикальное изменение температуры by Wikipedia
На приведенном выше графике использовалось уравнение Лоренца. Начальные условия для x и z остались прежними, но y были изменены между 1,001, 1,0001 и 1,00001. Значения ро, сигмы и бета составили 45,9.2, 16 и 4 соответственно.
Как видно из графика, даже малейшая разница в начальных значениях и приводит к значительным изменениям примерно через 12 итераций в трех случаях. Это пример чувствительной зависимости от начальных условий. Системы, чувствительные к начальным условиям, называются хаотическими, но недостаточно чувствительной зависимости только от начальных условий.
Изображение автора Рассмотрим систему, сгенерированную картой x → 1,5 x
Рассмотрим систему, сгенерированную картой x → 1,5 x С исходными x = 0,2 и исходными x =0,21. Обратите внимание, что после нескольких итераций красная и синяя линии начали двигаться сами по себе . Эта система чувствительна к начальным условиям, но не хаотична. Поскольку система умножает x на 1,5, любая небольшая разница между начальными точками увеличивается в 1,5 раза на каждой итерации. Независимо от начального условия, каждое начальное условие в конечном итоге будет приближаться к положительной или отрицательной бесконечности, поэтому асимптотическое поведение при заданном наборе начальных условий очень предсказуемо.
Топологическое смешение означает, что оно будет развиваться в одном и том же регионе в течение определенного периода времени, а затем, в конце концов, пересечется с любым другим данным регионом.
Изображение из ВикипедииНа приведенном выше графике показаны шесть итераций набора состояний x и y , пройденных через логистическую карту.
 Светло-синий (первая итерация) указывает на начальное состояние, которое образует круг. Видно, что с течением времени происходит перемешивание. Темно-синий (шестая итерация) показывает, что точки почти полностью разбросаны в фазовом пространстве.
Светло-синий (первая итерация) указывает на начальное состояние, которое образует круг. Видно, что с течением времени происходит перемешивание. Темно-синий (шестая итерация) показывает, что точки почти полностью разбросаны в фазовом пространстве.Это показывает, что две соседние точки в сложной системе в конечном итоге окажутся в очень разных позициях после некоторых итераций. Логистическая карта имеет следующее уравнение:
Изображение автора, иллюстрированное из ВикипедииЧтобы расширить пространство состояний логистической карты до двух измерений, было создано второе состояние следующим образом:
Изображение автора, иллюстрированное из ВикипедииПлотность Периодические орбиты означают, что каждая точка в фазовом пространстве произвольно близка к набору начальных условий. Простейшим примером систем с плотностью периодических орбит является одномерная логистическая карта, определяемая х → 4 х (1 — х ).
Изображение автораНа приведенном выше графике показаны 50 итераций логистической карты, определяемой как x → 2.
Изображение автора 1 x (1 — x ). Обратите внимание, что орбита притягивается к определенному значению примерно около 0,5 с течением времени.
1 x (1 — x ). Обратите внимание, что орбита притягивается к определенному значению примерно около 0,5 с течением времени.Теперь, если мы увеличим значение r до 3,1, чтобы логистическая карта определялась как x → 3,1 x (1 — x ). Обратите внимание, что орбита превращается в период из 2 циклов, поскольку значение циклично вокруг 0,7 и 0,5. Он называется 2-м циклом, потому что для завершения одного цикла требуется 2 итерации.
Изображение автораТеперь, если мы увеличим значение r до 3,5, чтобы логистическая карта определялась как x → 3,5 x (1 — x ), орбита превращается в период из 4 циклов. поскольку значение циклично вокруг 0,87, 0,38, 0,82 и 0,5. Как и раньше, это поведение является стабильным, потому что система циклически повторяет 4 значения и в конечном итоге с течением времени будет сходиться к этим значениям.
Изображение автораТеперь, если мы увеличим значение r до 4.
 Обратите внимание, что больше нет периодического поведения. Орбита никогда не повторяется точно так же. Такое поведение нестабильно, потому что орбита продолжает вращаться неравномерно. Следовательно, логистическая карта, определяемая x → 4 x (1 — x ) считается хаотическим, потому что орбита приближается к начальной точке сколь угодно близко, но никогда не сойдется к периодической орбите.
Обратите внимание, что больше нет периодического поведения. Орбита никогда не повторяется точно так же. Такое поведение нестабильно, потому что орбита продолжает вращаться неравномерно. Следовательно, логистическая карта, определяемая x → 4 x (1 — x ) считается хаотическим, потому что орбита приближается к начальной точке сколь угодно близко, но никогда не сойдется к периодической орбите.Странный аттрактор
Вспомните логистическую карту, о которой мы говорили. На самом деле это функция, определяемая:
Изображение автораКарта — это просто еще один способ сказать о функции. Как мы видели ранее, эта функция создает хаос при определенном параметре r .
Изображение автораНа приведенном выше графике показано начальное состояние 0,2 для нескольких значений р. Зеленая линия, полученная при значении r , равном 0,5, со временем сходится к 0. Аналогичное поведение происходит с синей, черной, фиолетовой и коричневой линией, они сходятся к определенному значению.
Изображение автора
Даже если мы изменим начальный x синей линии на 0,9, она все равно сходится к определенному значению с течением времени. Такая величина называется аттрактором .
Изображение автораОранжевая линия, которая имеет значение r , равное 3,5, система колеблется между четырьмя значениями и в конечном итоге сходится к этим значениям. Этот аттрактор называется предельным циклом .
Изображение автораКрасная линия со значением r , равным 4,0, приводит к хаотическому поведению, как мы упоминали ранее. Эта система имеет странный аттрактор , вокруг которого система колеблется вечно, никогда не повторяясь в точности так же. В приведенном выше примере x превращается в 0,611 после 50 итераций. Состояние на последней итерации называется конечным состоянием .
Бифуркация
Те графики, которые мы видели ранее, показывают, как x изменяется со временем при различных значениях r , но мы видели только r из 0,5, 1,0, 1,5, 2,0, 2,5, 3,0, 3,05 и 3,05 и r .
Изображение автора . Для дальнейшего изучения мы создадим бифуркационную диаграмму . Бифуркация — это еще один термин для разделения на две части. Ось X равна r значение от 0,0 до 4,0, а ось Y составляет x в конечном состоянии каждого r .
. Для дальнейшего изучения мы создадим бифуркационную диаграмму . Бифуркация — это еще один термин для разделения на две части. Ось X равна r значение от 0,0 до 4,0, а ось Y составляет x в конечном состоянии каждого r .На приведенном выше графике показано разделение периодов стабильных орбит от 1 к 2, к 4, к 8, к 16, к 32 и т. д. Если мы посмотрим ближе к интервалу r между 2,7 и 3,3, он показывает:
Изображение автораОбратите внимание, что разделение происходит, когда r приближается к 3.0. Вспомните красочные графики, о которых мы говорили ранее, это на самом деле серая линия, имеющая 2 точки.
Изображение автораТеперь мы смотрим ближе к r между 3,35 и 3,525, другое разделение происходит вокруг r значение 3,449. Следовательно, оранжевая линия на нашем предыдущем графике имеет период 4.
Изображение автораУвеличьте еще больше, и теперь мы видим, что другое разделение происходит вокруг r со значением 3,544.
 Обратите внимание на периодическую модель? от 2 до 4 и теперь 8 периодов, это называется удвоение периода . Выбрав определенное значение r мы можем получить любой период, какой захотим, если он равен степени двойки, потому что он каждый раз удваивается. Если мы увеличим масштаб до следующей ветви, мы увидим период 16, а затем он будет удваиваться по мере увеличения значения r . Неважно, насколько сильно мы увеличиваем масштаб, мы будем видеть один и тот же паттерн снова и снова, поэтому он считается фракталом . К сожалению, наш график имеет низкое качество и не может показать его четко.
Обратите внимание на периодическую модель? от 2 до 4 и теперь 8 периодов, это называется удвоение периода . Выбрав определенное значение r мы можем получить любой период, какой захотим, если он равен степени двойки, потому что он каждый раз удваивается. Если мы увеличим масштаб до следующей ветви, мы увидим период 16, а затем он будет удваиваться по мере увеличения значения r . Неважно, насколько сильно мы увеличиваем масштаб, мы будем видеть один и тот же паттерн снова и снова, поэтому он считается фракталом . К сожалению, наш график имеет низкое качество и не может показать его четко.Константы Фейгенбаума
Вспомните бифуркационную диаграмму, которую мы создали ранее. Точки разделения расположены неравномерно, вместо этого они становятся все меньше и меньше, как р увеличивается.
Изображение автораВысота и ширина вил уменьшаются в постоянном соотношении. Отношение ∆1 к ∆2 примерно такое же, как ∆2 к ∆3.
 Это отношение приближается к значению 4,669, что означает, что отношение ∆1 к ∆2 близко к 4,669, а ∆2 к ∆3 еще ближе к 4,669, и так далее. Фейгенбаум доказал соотношение, и оно названо в честь его имени , константа Фейгенбаума . Что интересно, константа Фейгенбаума универсальна, означает, что она имеет одинаковое значение для всех функций f(x), которые отображают интервал в себя и имеют один квадратичный максимум. Постоянная Фейгенбаума оказывается очень важной константой в математике. Это аналог π в геометрии и e в исчислении.
Это отношение приближается к значению 4,669, что означает, что отношение ∆1 к ∆2 близко к 4,669, а ∆2 к ∆3 еще ближе к 4,669, и так далее. Фейгенбаум доказал соотношение, и оно названо в честь его имени , константа Фейгенбаума . Что интересно, константа Фейгенбаума универсальна, означает, что она имеет одинаковое значение для всех функций f(x), которые отображают интервал в себя и имеют один квадратичный максимум. Постоянная Фейгенбаума оказывается очень важной константой в математике. Это аналог π в геометрии и e в исчислении.Множество Мандельброта
Изображение из ВикипедииМножество Мандельброта — один из самых красивых фракталов в математике. Это набор значений c в комплексной плоскости, для которых орбита 0 при итерации квадратичного отображения остается ограниченной.
Изображение автора из ВикипедииПри начальных z = 0 комплексное число c является частью множества Мандельброта, если значение z_t остается ограниченным независимо от того, сколько мы повторяем функцию.
Изображение из Википедии Если число увеличивается до бесконечности, это означает, что c не является частью множества Мандельброта.
Если число увеличивается до бесконечности, это означает, что c не является частью множества Мандельброта.На приведенном выше графике показано значение множества Мандельброта, черная область указывает на то, что c является частью множества Мандельброта.
Изображение автораНапример, c = 1 в правом углу графика не является частью множества Мандельброта, потому что с течением времени оно будет увеличиваться до бесконечности.
Изображение автораВопреки этому, -1 находится в черной области, что означает, что это часть множества Мандельброта, оно колеблется между 2 значениями -1 и 0. Но какое это имеет отношение к хаосу?
Изображение от Jonny HymanБифуркация на самом деле находится под множеством Мандельброта. Все числа в основной кардиоиде (тот самый большой круг) сходятся к определенному значению, аналогичному значению r между 0 и 3 в разветвлении. Все числа на основном диске колеблются между двумя значениями, это аналогично тому, что r значение между 3 и 3,44 в бифуркации, они имеют период 2.
 Удвоение периода продолжается по мере того, как мы уменьшаем c и в конечном итоге попадаем в хаос, точно так же, как мы увеличиваем r в бифуркации .
Удвоение периода продолжается по мере того, как мы уменьшаем c и в конечном итоге попадаем в хаос, точно так же, как мы увеличиваем r в бифуркации . Заключение
Каждое решение, которое вы принимали за всю свою жизнь, побуждало вас прочитать эту статью.
Литература
Аттрактор
В математической области динамических систем аттрактор — это набор числовых значений, к которым система стремится…
en.wikipedia.org
Что такое Теория Хаоса?
Хаос — это наука неожиданностей, нелинейности и непредсказуемости. Он учит нас ожидать неожиданного…
fractalfoundation.org
теория хаоса | Определения и факты
Теория хаоса в механике и математике, изучение явно случайного или непредсказуемого поведения систем…
www.britannica.com
Теория хаоса | Великолепная математика и естественные науки Wiki
Теория хаоса — это исследование определенного типа систем, возникших из некоторых начальных условий.
 Небольшой…
Небольшой…блестящий.org
Эффект бабочки: все, что вам нужно знать об этой мощной ментальной модели
Эффект бабочки — это часто неправильно понимаемое явление, при котором небольшое изменение начальных условий может привести к…
fs.blog
Теория хаоса
Теория хаоса изучает динамические системы, чрезвычайно чувствительные к начальным условиям. Если бы мы…
mathsbyagirl.wordpress.com
Система Лоренца
Система Лоренца — это система обыкновенных дифференциальных уравнений, впервые изученная Эдвардом Лоренцем и Эллен Феттер. Это…
en.wikipedia.org
Логистическая карта
Логистическая карта представляет собой полиномиальное отображение (эквивалентно, рекуррентное отношение) степени 2, часто упоминаемое как архетип…
en.wikipedia.org
Орбита (динамика)
В математике при изучении динамических систем орбитой называется совокупность точек, связанных функцией эволюции…
en.
 wikipedia.org
wikipedia.orgХаос в одном невинном уравнении
Что такое хаос?
medium.com
Теория хаоса и логистическая карта
Использование Python для визуализации хаоса, фракталов и самоподобия для лучшего понимания границ знаний и…
В математике, в частности в теории бифуркаций, константы Фейгенбаума — это две математические константы, которые обе…
en.wikipedia.org
Логистическая карта
В этом Флонге будет обсуждаться одна из самых известных динамических систем, логистическая карта. Логистическая карта-это…
www.complexity-explorables.org
Mitchell Feigenbaum (1944–2019), 4.66920160910299067185320382 … Степен Wolfram Phisonings
9000 82. И это проявляется довольно повсеместно в определенных видах…writings.stephenwolfram.com
Логические ребра — * Бифуркационные диаграммы и константа Фейгенбаума
Выбирается начальное значение x между 0 и 1.
 Приведенный выше расчет повторяется много раз, что дает ряд…
Приведенный выше расчет повторяется много раз, что дает ряд…site.google.com
Единственное уравнение, которое правит миром
Уравнение связывает возбуждение нейронов, конвекцию жидкости, множество Мандельброта и многое другое. обязательно изменится…
medium.com
Numberphile
Это Numberphile. В основном мы публикуем видео о математике и вообще о цифрах.
www.numberphile.com
Complexity Explorer
Complexity Explorer предоставляет онлайн-курсы, учебные пособия и ресурсы, необходимые для изучения сложных систем…
www.complexityexplorer.org
3009005 Сентябрь 2006 г. Еще в 1970-х и 1980-х годах математики, работающие в области, называемой динамическими системами, использовали…plus.maths.org
Это уравнение изменит ваш взгляд на мир — Veritasium
Логистическая карта объединяет популяции животных, конвекцию жидкости, активацию нейронов, множество Мандельброта и многое другое…
www.
 veritasium.com
veritasium.comЭдвард Лоренц | Биография, теория хаоса, эффект бабочки и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
 Рассмотрим систему, сгенерированную картой x → 1,5 x
Рассмотрим систему, сгенерированную картой x → 1,5 x 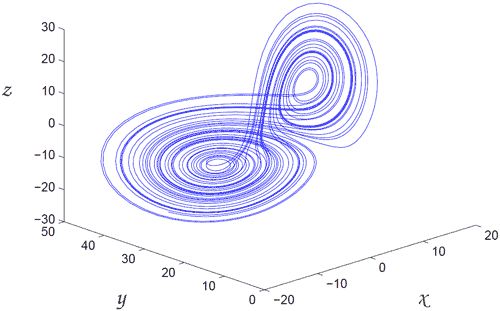 Светло-синий (первая итерация) указывает на начальное состояние, которое образует круг. Видно, что с течением времени происходит перемешивание. Темно-синий (шестая итерация) показывает, что точки почти полностью разбросаны в фазовом пространстве.
Светло-синий (первая итерация) указывает на начальное состояние, которое образует круг. Видно, что с течением времени происходит перемешивание. Темно-синий (шестая итерация) показывает, что точки почти полностью разбросаны в фазовом пространстве. 1 x (1 — x ). Обратите внимание, что орбита притягивается к определенному значению примерно около 0,5 с течением времени.
1 x (1 — x ). Обратите внимание, что орбита притягивается к определенному значению примерно около 0,5 с течением времени.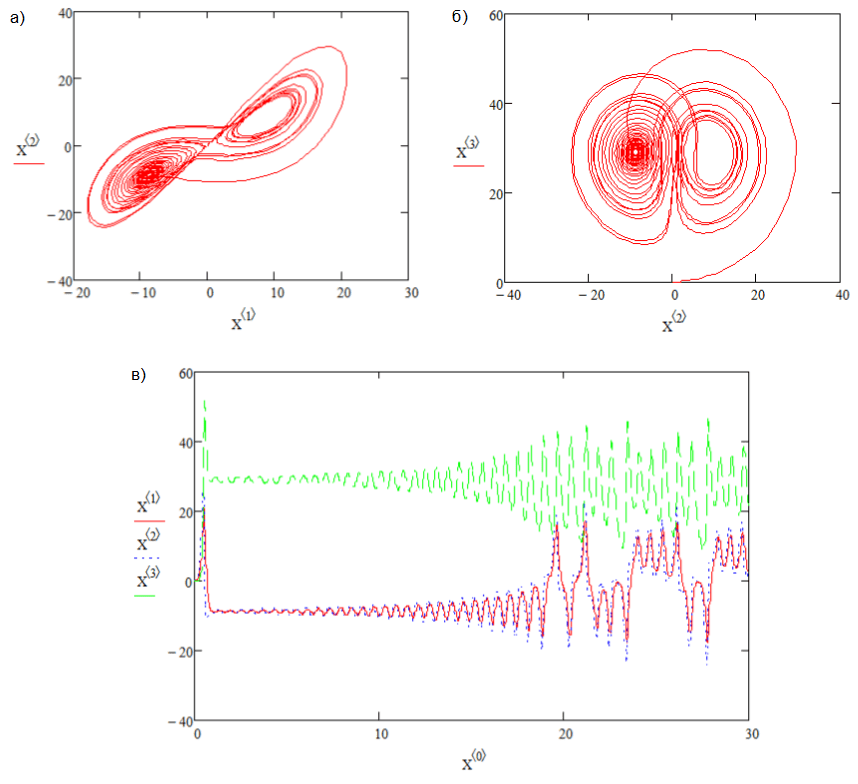 Обратите внимание, что больше нет периодического поведения. Орбита никогда не повторяется точно так же. Такое поведение нестабильно, потому что орбита продолжает вращаться неравномерно. Следовательно, логистическая карта, определяемая x → 4 x (1 — x ) считается хаотическим, потому что орбита приближается к начальной точке сколь угодно близко, но никогда не сойдется к периодической орбите.
Обратите внимание, что больше нет периодического поведения. Орбита никогда не повторяется точно так же. Такое поведение нестабильно, потому что орбита продолжает вращаться неравномерно. Следовательно, логистическая карта, определяемая x → 4 x (1 — x ) считается хаотическим, потому что орбита приближается к начальной точке сколь угодно близко, но никогда не сойдется к периодической орбите.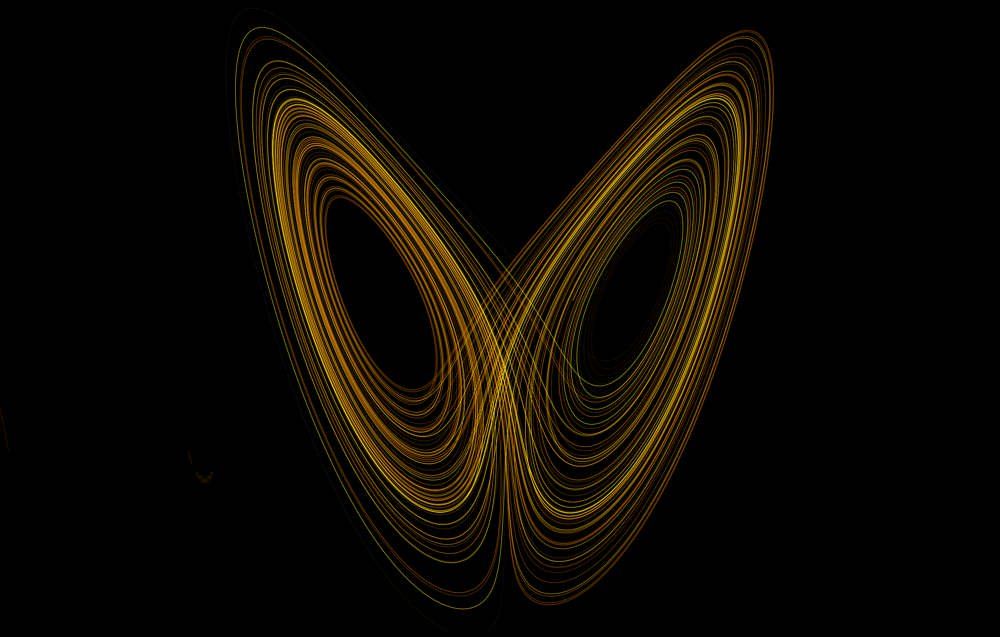
 . Для дальнейшего изучения мы создадим бифуркационную диаграмму . Бифуркация — это еще один термин для разделения на две части. Ось X равна r значение от 0,0 до 4,0, а ось Y составляет x в конечном состоянии каждого r .
. Для дальнейшего изучения мы создадим бифуркационную диаграмму . Бифуркация — это еще один термин для разделения на две части. Ось X равна r значение от 0,0 до 4,0, а ось Y составляет x в конечном состоянии каждого r . Обратите внимание на периодическую модель? от 2 до 4 и теперь 8 периодов, это называется удвоение периода . Выбрав определенное значение r мы можем получить любой период, какой захотим, если он равен степени двойки, потому что он каждый раз удваивается. Если мы увеличим масштаб до следующей ветви, мы увидим период 16, а затем он будет удваиваться по мере увеличения значения r . Неважно, насколько сильно мы увеличиваем масштаб, мы будем видеть один и тот же паттерн снова и снова, поэтому он считается фракталом . К сожалению, наш график имеет низкое качество и не может показать его четко.
Обратите внимание на периодическую модель? от 2 до 4 и теперь 8 периодов, это называется удвоение периода . Выбрав определенное значение r мы можем получить любой период, какой захотим, если он равен степени двойки, потому что он каждый раз удваивается. Если мы увеличим масштаб до следующей ветви, мы увидим период 16, а затем он будет удваиваться по мере увеличения значения r . Неважно, насколько сильно мы увеличиваем масштаб, мы будем видеть один и тот же паттерн снова и снова, поэтому он считается фракталом . К сожалению, наш график имеет низкое качество и не может показать его четко.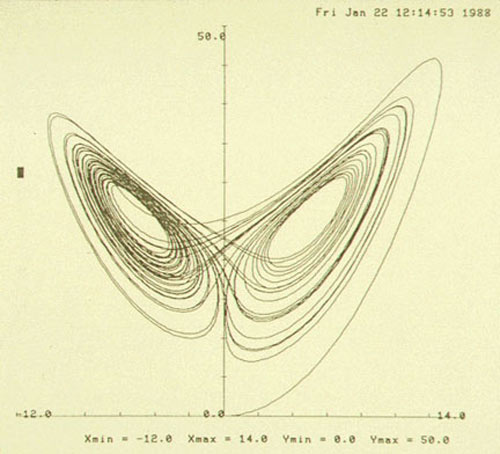 Это отношение приближается к значению 4,669, что означает, что отношение ∆1 к ∆2 близко к 4,669, а ∆2 к ∆3 еще ближе к 4,669, и так далее. Фейгенбаум доказал соотношение, и оно названо в честь его имени , константа Фейгенбаума . Что интересно, константа Фейгенбаума универсальна, означает, что она имеет одинаковое значение для всех функций f(x), которые отображают интервал в себя и имеют один квадратичный максимум. Постоянная Фейгенбаума оказывается очень важной константой в математике. Это аналог π в геометрии и e в исчислении.
Это отношение приближается к значению 4,669, что означает, что отношение ∆1 к ∆2 близко к 4,669, а ∆2 к ∆3 еще ближе к 4,669, и так далее. Фейгенбаум доказал соотношение, и оно названо в честь его имени , константа Фейгенбаума . Что интересно, константа Фейгенбаума универсальна, означает, что она имеет одинаковое значение для всех функций f(x), которые отображают интервал в себя и имеют один квадратичный максимум. Постоянная Фейгенбаума оказывается очень важной константой в математике. Это аналог π в геометрии и e в исчислении. Если число увеличивается до бесконечности, это означает, что c не является частью множества Мандельброта.
Если число увеличивается до бесконечности, это означает, что c не является частью множества Мандельброта. Удвоение периода продолжается по мере того, как мы уменьшаем c и в конечном итоге попадаем в хаос, точно так же, как мы увеличиваем r в бифуркации .
Удвоение периода продолжается по мере того, как мы уменьшаем c и в конечном итоге попадаем в хаос, точно так же, как мы увеличиваем r в бифуркации .  Небольшой…
Небольшой…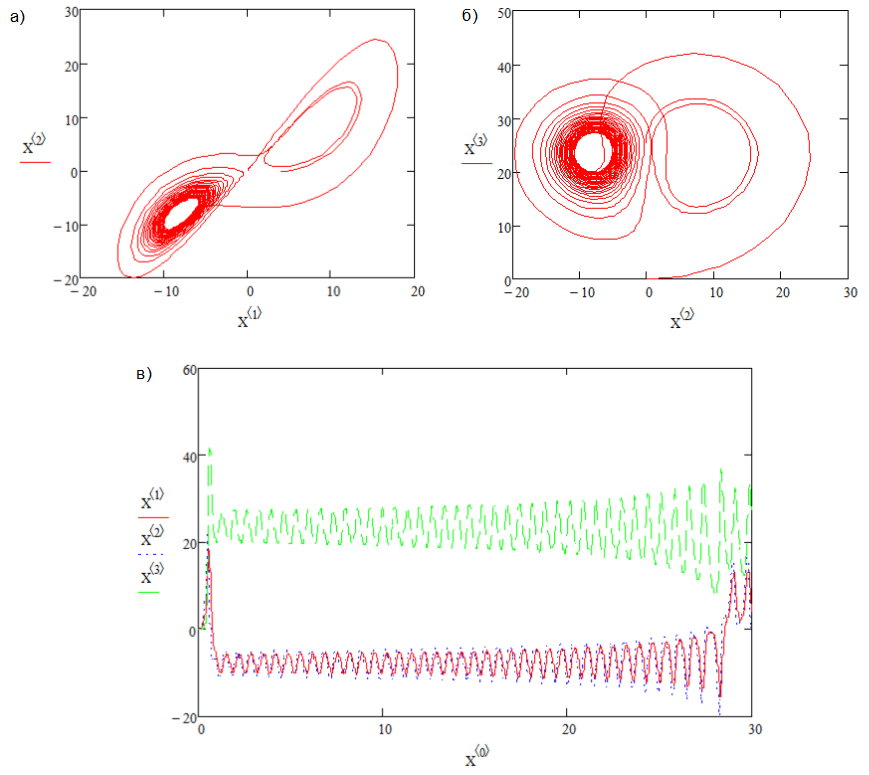 wikipedia.org
wikipedia.org Приведенный выше расчет повторяется много раз, что дает ряд…
Приведенный выше расчет повторяется много раз, что дает ряд…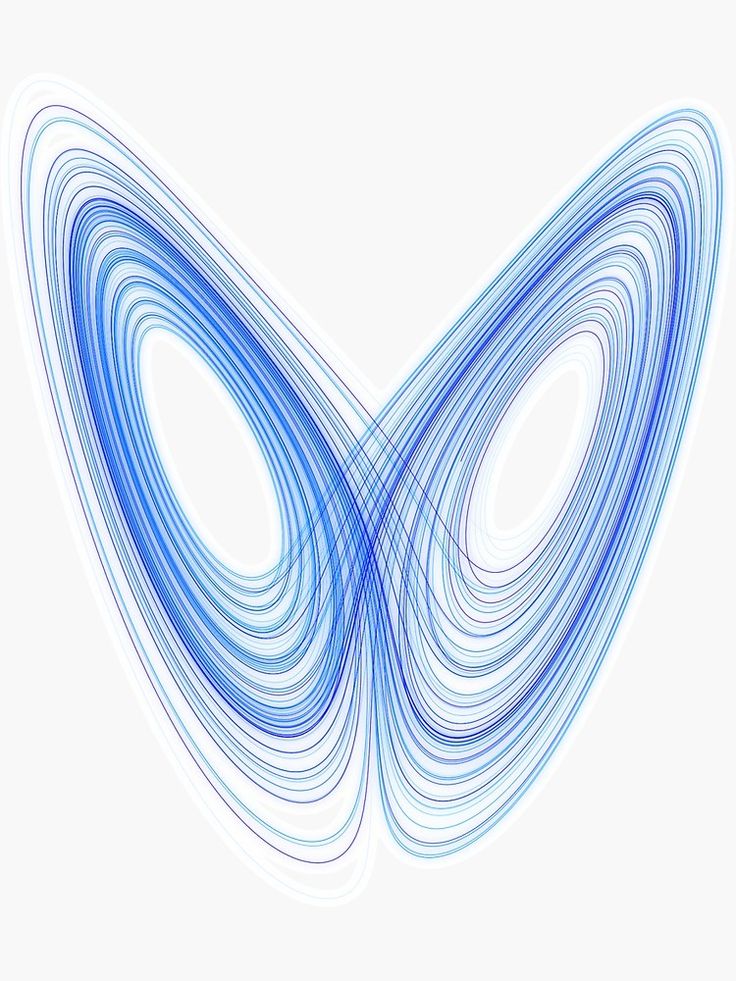 veritasium.com
veritasium.com