Вебер величина: HTTP status 402 — payment required, требуется оплата

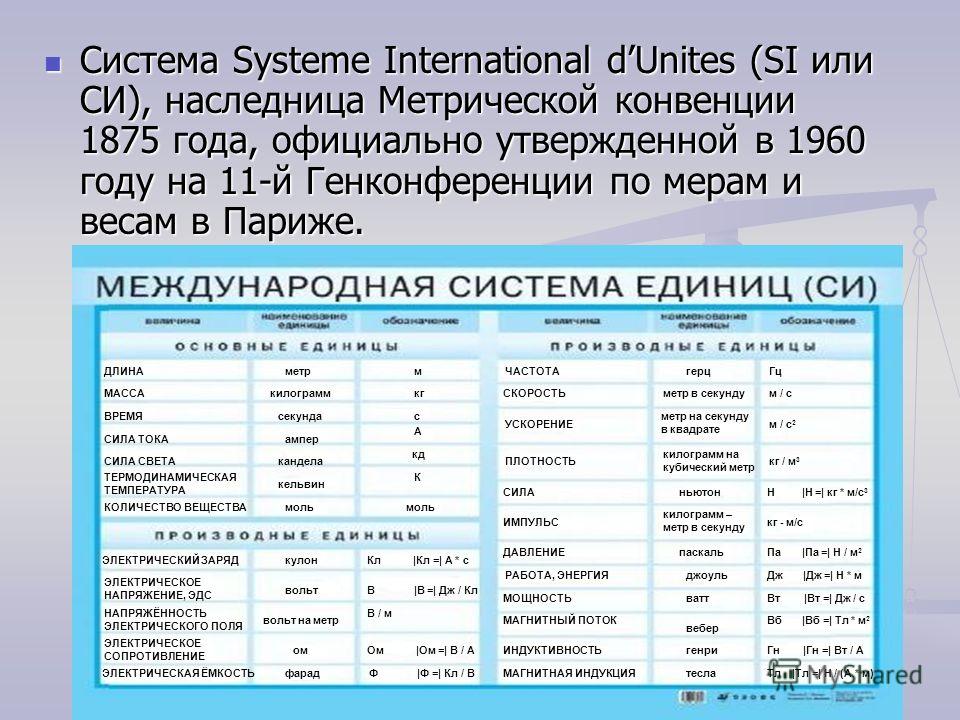
Единица измерения магнитного потока, теория и онлайн калькуляторы

Единица измерения магнитного потока, теория и онлайн калькуляторы

Определение

Элементарный магнитный поток ($dФ$) сквозь малую поверхность $dS$ равен произведению проекции вектора магнитной индукции ($B_n$) на нормаль к элементарной площадке $dS$ на величину этой площадки:

\[dФ=B_ndS\ \left(1\right).\]

Полный поток сквозь всю поверхность $S$ будет равен:

\[Ф=\int\limits_S{B_ndS\ \left(2\right).}\]

Если поверхность $S$ является плоской, находится она в однородном магнитном поле, причем перпендикулярно линиям индукции поля, то магнитный поток можно найти как:

\[Ф=BS\ \left(3\right).\]

Вебер — единица измерения магнитного потока в системе СИ

Единицу измерения магнитного потока можно определить исходя из выражения (3), как:

\[\left[Ф\right]=Тл\cdot м^2=Вб. 5Мкс$

Читать дальше: единица измерения магнитной индукции.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Предложение Вебера | Наука и жизнь

Отрывок из книги М. Бертолотти «История лазера» (журнальный вариант). — Долгопрудный: ИД «Интеллект», 2015.

Наука и жизнь // Иллюстрации

Американский физик Джозеф Вебер (Joseph Weber) прочёл первую публичную лекцию о принципах работы мазеров и лазеров. Известен также тем, что первым попытался детектировать гравитационные волны.Фото: National Institute of Biomedical Imaging and Bioengineering (NIBIB)/Wikimedia Commons/PD.

‹

›

Открыть в полном размере

Первое изложение на публике основного принципа, на котором может работать мазер (однако без самого работающего устройства), сделал Джозеф Вебер (1919—2000) в Оттаве (Канада) в 1952 году на конференции по электронным лампам (Electron Tube Research Conference). Это была престижная конференция, в которой участвовали лишь по приглашениям и на которой часто представляли идеи новых устройств.

Вебер был тогда молодым профессором электротехники университета Мэриленда и консультантом Военно-морской лаборатории США. Он получил диплом в Аннаполисе и стал первым квалифицированным инженером в области микроволн в отделе электронного противодействия флота. Здесь он имел возможность оценить технологическую важность усилителей с высокой чувствительностью к микроволновым и миллиметровым волнам, способных обнаруживать слабые волны от радаров. Информация о длинах волн, на которых работает радар, и их источнике позволяла затем посылать сигналы, ослепляющие вражеские приёмники, тем самым не позволяя врагу определять цели.

Идея мазера появилась у Вебера после лекции Карла Герцфельда (1892—1978) о вынужденном излучении. В 1951 году Вебер получил докторскую степень по физике, работая в области микроволновой спектроскопии, и стал профессором в университете Мэриленда. Здесь он продолжал работы по микроволновой спектроскопии.

Механизм процессов поглощения и испускания, которые возникают, когда излучение взаимодействует с газом, всегда интересовал учёного. В типичном эксперименте микроволновой спектроскопии микроволны от некоторого источника попадают на приёмник. Если между источником и приёмником располагается газ, то можно наблюдать поглощение некоторой части падающего излучения. Какова природа этого поглощения? Оно происходит, если молекулы газа обладают парой уровней и разность энергий между ними, делённая на постоянную Планка, приблизительно равна частоте микроволн.

Чтобы лучше понять, как это происходит, Вебер рассматривал систему только с двумя энергетическими уровнями, E₁ и Е₂ (причём Е₂ > E₁), на каждом из которых имеется число атомов или молекул соответственно n₁ и n₂ (мы будем называть n₁ и n₂ населённостями энергетических уровней E₁ и Е₂ соответственно). Когда микроволновая частота имеет правильное значение, поглощённая мощность пропорциональна населённости первого уровня, то есть n₁. Частицы, находящиеся на верхнем уровне 2, в свою очередь, испускают вынужденное излучение на той же частоте, мощность которого пропорциональна n₂. Итоговая мощность равна разности между поглощённой и испущенной мощностью, то есть пропорциональна n₁–n₂. Поскольку при термическом равновесии n₁ всегда больше, чем n₂, Вебер заключил, что «эта итоговая мощность всегда положительная величина. Поэтому в обычных условиях мы получаем поглощение излучения». Однако, добавлял он, «мы можем получить усиление, если каким-нибудь способом сделаем число осцилляторов в верхнем состоянии бoльшим, чем число их в нижнем состоянии», и заключал, что «способ осуществить это предложен в эксперименте Парселла по отрицательной температуре».

Эти рассуждения Вебер представил на конференции в 1952 году. Позднее он объяснял, что намеревался опубликовать свои результаты в широко читаемом журнале. Но профессор Г. Рейх из Йельского университета написал ему, что он, будучи председателем конференции в 1952 году, является также редактором журнала (не широко читаемого, по мнению Вебера) и предполагает опубликовать в нём материалы конференции. В результате краткое сообщение в виде аннотации к докладу было опубликовано в июньском номере 1953 года «Transaction of the Institute of Radio Engineers Professional Group on Electron Devices».

В докладе Вебер подчёркивал, что усиление является когерентным. Метод, который он предлагал для получения инверсной населённости, фактически никогда не был осуществлён на практике. И даже казалось маловероятным, чтобы его можно было реализовать. Более того, Вебера интересовал только усилитель. Идея обратной связи, столь существенная в мазере Таунса, как мы увидим, не представляла важности для Вебера, и он не обсуждал её.

Вебер даже оценил количественно возможности усилителя, но расчёты, полученные им, показали столь слабые характеристики, что он решил оставить эту затею и не пытался построить что-либо. Однако идея вызвала определённый интерес, и после представления работы на конференции Вебер был приглашён RCA провести семинар по своей идее, за который получил гонорар $50. После того семинара Чарлз Таунс написал ему письмо с просьбой прислать копию статьи. Однако Таунс не ссылался на работу Вебера в своих первых работах, хотя сделал это позже.

Попытки Вебера отмечены IRE (Institute of Radio Engineers) в 1958 году за «его раннее установление концепции, приводящей к мазеру».

От редакции. В 1964 году Нобелевская премия по физике «за фундаментальные работы в области квантовой электроники, которые привели к созданию излучателей и усилителей на лазерно-мазерном принципе» была присуждена Ч. Таунсу, Н. Г. Басову и А. М. Прохорову.

Информация о книгах Издательского дома «Интеллект» — на сайте www.id-intellect.ru

Вебер Эрнст Генрих



	Вебер Эрнст Генрих
1795-1878	БИОГРАФИЧЕСКИЙ УКАЗАТЕЛЬ
 XPOHOC ВВЕДЕНИЕ В ПРОЕКТ ФОРУМ ХРОНОСА НОВОСТИ ХРОНОСА БИБЛИОТЕКА ХРОНОСА ИСТОРИЧЕСКИЕ ИСТОЧНИКИ БИОГРАФИЧЕСКИЙ УКАЗАТЕЛЬ ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ ГЕНЕАЛОГИЧЕСКИЕ ТАБЛИЦЫ СТРАНЫ И ГОСУДАРСТВА ЭТНОНИМЫ РЕЛИГИИ МИРА СТАТЬИ НА ИСТОРИЧЕСКИЕ ТЕМЫ МЕТОДИКА ПРЕПОДАВАНИЯ КАРТА САЙТА АВТОРЫ ХРОНОСА Родственные проекты: РУМЯНЦЕВСКИЙ МУЗЕЙ ДОКУМЕНТЫ XX ВЕКА ИСТОРИЧЕСКАЯ ГЕОГРАФИЯ ПРАВИТЕЛИ МИРА ВОЙНА 1812 ГОДА ПЕРВАЯ МИРОВАЯ СЛАВЯНСТВО ЭТНОЦИКЛОПЕДИЯ АПСУАРА РУССКОЕ ПОЛЕ	Эрнст Генрих Вебер Вебер (Weber) Эрнст Генрих (1795-1878) — немецкий анатом и физиолог, один из основоположников научной психологии, внесший в нее идею измерения. Биография. С 1818 г. — профессор анатомии, с 1840 г. — профессор физиологии Лейпцигского университета; изучал тормозящее влияние блуждающего нерва на деятельность сердца (1845). Иностранный член-корреспондент Петербургской академии наук (1869). Исследования. Проводил исследования в области физиологии органов чувств: слуха, зрения, кожной чувствительности. Исследовал эффект температурной адаптации: если сначала поместить одну руку в прохладную воду, а другую — в горячую, то теплая вода после этого будет казаться для первой руки более теплой, чем для второй. Анализ осязания («Об осязании») позволил ему выделить три вида кожных ощущений: ощущение давления или прикосновения, температурные ощущения, ощущения локализации. Разработал схему экспериментального исследования осязания, для чего сконструировал по типу циркуля особый прибор («эстезиометр», или «циркуль Вебера»), при помощи которого оценивал расстояние, достаточное для того, чтобы два прикосновения к поверхности кожи не сливались в одном ощущении. В этих исследованиях Вебер определил, что данное расстояние различно для различных участков кожи (так называемые «круги ощущения») и, следовательно, кожа обладает разной чувствительностью. В 1834 г. провел свои всемирно известные исследования соотношений ощущений и раздражителей, показавшие, что новый раздражитель, чтобы восприниматься как отличающийся, должен в действительности отличаться на определенную величину от исходного и что эта величина представляет собой постоянную про-порцию от исходного раздражителя. Это было отражено им в следующей формуле: ΔJ /J = К, где J — исходный раздражитель, ΔJ — отличие нового раздражителя от исходного, К— константа, зависящая от типа рецептора. Так, в частности, чтобы два чистых звука воспринимались как различные, новый звук должен отличаться от исходного на 1/10 величины, в случае разных весов новый вес должен отличаться на 1/30,  а для световых раздражителен эта пропорция — 1/100. На основе данных исследований Г. Фехнером была выведена формула основного закона психофизики: ощущение изменяется пропорционально логарифму раздражителя (закон Вебера—Фехнера). Кроме того, Вебер высказывал интересные соображения по поводу сензитивности раннего детского возраста для билатерального переноса двигательных навыков (сам он обладал способностью рисовать зеркальные изображения одновременно обеими руками). Кондаков И.М. Психология. Иллюстрированный словарь. // И.М. Кондаков. – 2-е изд. доп. И перераб. – СПб., 2007, с. 90-91. Далее читайте: Исторические лица Германии (биографический справочник). Сочинения: De aure et auditu hominis ct animalum. 1820; De pulsu. resorplione. auditu ct tactu. Leipzig, 1834. Der Tastsinn und Gemeindegefuhl. 1846; Uber den Raunisimi und die Empfindungskreise in der Haut und die Auge. 1952. Литература: Ярошевскии M. Г. История психологии. 3-е над. М, 1985; Э. Г. Вебер// Психология: Биографический библиографический словарь / Под ред. Н. Шихи, Э. Дж. Ченмана У. А. Конроя. СПб.: Евразия, 1999.
	ХРОНОС: ВСЕМИРНАЯ ИСТОРИЯ В ИНТЕРНЕТЕ
	ХРОНОС существует с 20 января 2000 года, Редактор Вячеслав Румянцев При цитировании давайте ссылку на ХРОНОС

Глава 23.

Закон электромагнитной индукции

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

(23. 1)

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м² однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

(23.2)

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле.

Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

(23.3)

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

(23.4)

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

(23.5)

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3).

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23. 2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).

Вебер Фехнер

Закон фехнером закон, согласно коему величина ощущения прямопропорциональна логарифму интенсивности раздражителя — то есть возрастание силы раздражения вгеометрической прогрессии соответствует росту ощущения в арифметической прогрессии.  Эта формулаизмерения ощущений была выведена на основе исследований Вебера, где было показано постоянствоотносительной величины приращения раздражителя, вызывающего ощущение едва заметного различия.При этом был введен его собственный постулат о том, что едва заметный прирост ощущения являетсявеличиной постоянной и его можно применять использовать как единицу измерения ощущения.

Ключевую роль в точной формулировке второй интересующей нас закономерности сыграл тот самый Густав Фехнер, основатель психофизиологии, об опытах которого мы говорили в предыдущем Прологе. Эта закономерность — её сегодня называют законом Вебера-Фехнера — связывает физическую интенсивность какого-либо стимула с субъективной реакцией на этот стимул. Например, стимулом может быть громкий звук или вспышка света меняющейся интенсивности. Реакция на стимул — субъективная оценка его интенсивности или сила реакции организма на него.

Закон Вебера-Фехнера записывается так:

тут S — физическая или объективная интенсивность стимула, S_min — пороговая интенсивность, обозначающая нижний предел чувствительности органов чувств, R — интенсивность субъективной или органической реакции на стимул (о том, как она измеряется, чуть дальше), k — некоторый коэффициент, величина которого зависит от индивидуума и канала восприятия. Отметим, что интенсивность реакции зависит от отношения S/S_min, которое можно понимать как интенсивность стимула, рассчитанная в минимальных значимых единицах.

Легко заметить, что по своей форме этот закон в точности соответствует уравнению субъективной ценности Бернулли. На это сходство обратил внимание ещё сам Фехнер, цитируя Бернулли. Сегодня принято считать, что это не просто сходство, а выражение одной и той же закономерности человеческого восприятия — ведь количество товара в уравнении Бернулли можно трактовать как интенсивность стимула, а его субъективную ценность — как интенсивность реакции на стимул.

Любопытно, что Фехнер вывел своё уравнение отнюдь не исходя из общих соображений, как Бернулли (хотя, в принципе, мог бы). Он проанализировал результаты, полученные другим немецким физиологом, Эрнстом Вебером. В середине 19-го века этот ученый изучал особенности человеческого восприятия веса различных грузов, и обнаружил интересную закономерность. Отвлекаясь от конкретных цифр Вебера, она такова: если испытуемый держал в руке груз весом в 100 гр., он не замечал прибавки в 5 гр., но замечал прибавку в 10 гр. Однако, если испытуемый держал в руке груз весом в 200 гр., он не замечал прибавки в 10 гр., а лишь прибавку в 20 гр. Иными словами, минимальная заметная прибавка к весу груза оказалась прямо пропорциональной его исходному весу. Вебер выяснил, что эта закономерность действует довольно в широких пределах в восприятии веса, силы звука, яркости и т.д. Серьезные отклонения от неё наблюдались лишь при очень слабых и очень сильных интенсивностях стимулов. Математический анализ результатов Вебера и привёл Фехнера к выражению, один-в-один похожему на уравнение Бернулли.

Обратим внимание, что Вебер не просил своих испытуемых как-то субъективно оценивать вес грузов, он просил лишь отмечать тот момент, когда они фиксируют изменение веса. Это значит, что выделенная закономерность относится не к каким-то высокоуровневым психологическим особенностям восприятия и мышления — как это можно счесть исходя из закона Бернулли — а характеризует довольно низкоуровневые, первичные процессы восприятия. Более того, закон Вебера-Фехнера действует даже там, где наше восприятие, вроде бы, вообще ни причем. В частности, если в качестве стимула используется инъекция гормона, то интенсивность физиологической реакции организма на инъекцию также подчиняется этому закону. То есть, возможно, что закон Вебера-Фехнера относится не к особенностям восприятия органами чувств, а вообщеописывает реакцию человека и его организма на любого рода внешние воздействия.

Но закон Вебера-Фехнера действует не только на человека. Ещё в 20-х годах прошлого века были получены свидетельства , что ему подчиняются и насекомые. В частности, двигательная активность жуков Popillia Japonica увеличивается с увеличением интенсивности светового стимула в соответствии с законом Вебера-Фехнера.

У нас достаточно оснований, чтобы выдвинуть довольно смелую гипотезу:закономерность вида закона Вебера-Фехнера описывает интенсивность реакции любой сложной когнитивной системы на внешние стимулы — будь это организм человека или любая другая органическая или социальная система.

Может быть, этому закону подчиняются не только когнитивные или органические системы. Характеризуя интенсивность землятресений, обычно используют не линейную, а логарифмическую шкалу, шкалу Рихтера. Если интенсивность землетрясения сопоставлять с амплитудой максимальных колебаний поверхности земли A_max, то магнитуда землетрясения по Рихтеру вычисляется так:

Как минимум, шкала Рихтера гораздо лучше отражает субъективную силу землетрясений, лучше описывая масштаб разрушений и другие последствия стихии. Но причина может заключаться не столько в нашем восприятии, сколько в объективной мере масштаба разрушений, которая зависит не от интенсивности толчков, а от логарифма их интенсивности. В этом случае среда реагирует на толчки точно также, как и человек на внешние стимулы — в соответствии с законом Вебера-Фехнера.

+

7.1.2. Проблема измерения ощущений. Психофизика

Каждое ощущение независимо от его принадлежности к

определенной сенсорной системе, например зрению, слуху, осязанию и т.д.,

обладает свойствами интенсивности, длительности и

пространственной локализации.

Проблеме измерения соотношения объективной и субъективной

интенсивности стимула посвящен особый раздел психологии —

психофизика. Основателем психофизики считается Г.Т. Фехнер A801—

1887), опубликовавший в 1860 г. фундаментальный труд

«Элементы психофизики». В дальнейшем установлением количественной

меры ощущений занимались многие ученые.

Психофизика основывается на ряде эмпирических фактов. Во-

первых, легко видеть, что не всякий объективно воздействующий

физический раздражитель вызывает у нас ощущение. Во-вторых, мы

обладаем очень ограниченной способностью различать ощущения,

в то время как технический прибор точно показывает, что их

источники по физическим характеристикам отличаются. Например,

неподготовленному слушателю ноты «си» и «до» могут показаться

одинаковыми, хотя на самом деле они отличаются на целый тон. В-

третьих, даже в том случае, когда мы способны сказать, что одно

ощущение отличается по интенсивности от другого (свет свечи мы

видим как более слабый, чем свет настольной лампы), нам трудно

судить о конкретной величине этого различия. Так, мы не можем

сказать, что звук громкостью в 10 Дб (шорох листьев) в два раза

тише, чем звук громкостью в 20 Дб (шепот), а тот, в свою очередь, в

три раза тише, чем звук громкостью в 60 Дб (нормальный разговор).

Другими словами, объективная (физическая) шкала изменения

раздражителя не совпадает с субъективной шкалой изменения

ощущения. Поэтому возникает вопрос о психологических правилах

(законах) приведения в соответствие шкалы изменения раздражителя и

шкалы изменения ощущения. Фехнер и его последователи были

уверены, что данные соотношения носят не случайный характер, и

попытались описать эти закономерности математически.

Первая проблема, с которой приходится сталкиваться

исследователям, связана с фактом существования порога ощущений.

Выделяют абсолютный нижний и абсолютный верхний пороги

ощущений. Абсолютный нижний порог ощущения определяется

минимальной интенсивностью раздражителя, при котором возникает

соответствующее ощущение. Для установления значения нижнего

абсолютного порога (который различен для каждой модальности,

зависим от свойств анализатора и психологического состояния

человека) пользуются следующими приемами:

246 Глава 7. Познавательные процессы. Ощущение и восприятие

• постепенно увеличивая интенсивность стимула (например

громкость звука) от неощущаемой зоны до момента возникновения

ощущения (испытуемый сообщает, что «появился чуть слышный

звук»), экспериментатор фиксирует эту критическую точку, замеры

производятся несколько раз и вычисляется среднее значение;

• постепенно уменьшая интенсивность стимула (например,

громкость звука), двигаясь из отчетливо ощущаемой зоны к моменту

исчезновения ощущения (испытуемый сообщает «звук пропал»),

экспериментатор фиксирует это критическое значение, замеры

также производятся несколько раз и вычисляется среднее;

• вычисляют среднюю интенсивность раздражителя, в ответ на

который в 50% случаев фиксируется наличие ощущения, при этом

предъявление дискретных стимулов разной интенсивности

(близкой к зоне порога) осуществляется в случайном порядке с разными

интервалами, а испытуемый должен сообщать о каждом замеченным

им раздражителе.

Данные замеров, полученных разными методами, как правило,

несколько отличаются, что объясняется явлением адаптации и

эффектом ожидания.

Абсолютный верхний порог ощущения — это максимальная

интенсивность раздражителя, при котором ощущение теряет свою

модальную специфичность (часто переходя в боль). Так, для

слуховой чувствительности нижним абсолютным порогом будет

громкость примерно в 0,3 Дб (тиканье ручных часов в полной тишине на

расстоянии 6 м), а верхним абсолютным порогом — громкость в

150 Дб (шум взлетающего самолета). Следует заметить, что даже

для одного и того же человека величина абсолютного порога носит

непостоянный характер: он оказывается то выше, то ниже. Еще

И. Мюллер в середине XIX в. отмечал, что по мере накопления

опыта (тренировки) величина нижнего абсолютного порога

понижается, а по мере утомления — повышается. Влияние фактора

«тренированности» испытуемого на порог чувствительности его

сенсорных систем связано с тем, что человек начинает предвосхищать

нужные стимулы и поэтому легче находит их (в процесс ощущения

включаются механизмы восприятия).

Еще в большей степени эта неразрывность процессов ощущения

и восприятия проявилась в концепции «обнаружения сигнала»

Д. Грина и Дж. Светса A966). Они предположили, что вероятность

обнаружения слабого раздражителя, близкого по своему значению

к пороговому, зависит от «цены» ответа. Грин и Свете разделили два

типа ошибок — «ошибки пропуска» и «ложные тревоги».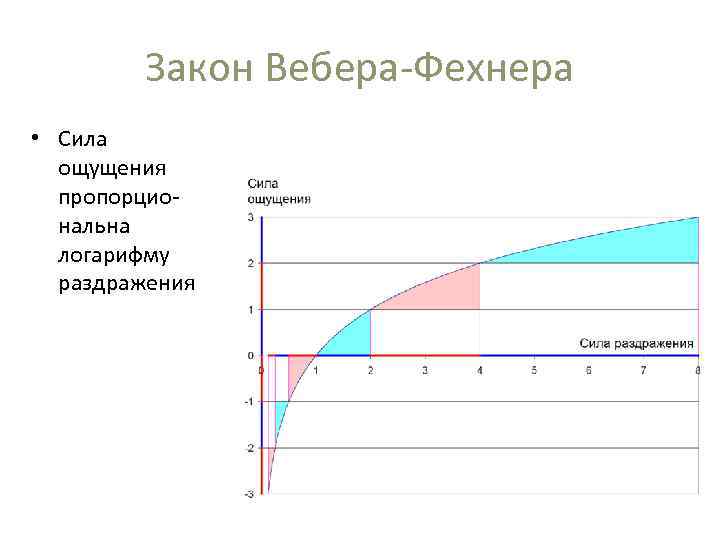 Первый

тип ошибки означает, что слабое ощущение присутствует в сознании

7.1. Ощущение

247

субъекта, но он не обнаруживает его и не дает реакции. Второй тип

ошибки проявляется в том, что субъект реагирует на ощущение,

которого объективно нет. Для иллюстрации концепции Грина и

Светса представим себе врача-диагноста. Он рассматривает

рентгенограмму больного и должен определить, свидетельствует ли она о

наличии опухоли. Если он пропустит тревожный сигнал, расплатой

может стать жизнь пациента. А если поднимет ложную тревогу,

пациенту придется всего лишь пройти процедуру повторного

обследования. Очевидно, что в такой ситуации врач скорее будет «замечать»

признаки опухоли в недостаточно определенном изображении, чем

игнорировать их (Дж. Лофтус (G. Loftus), 2002). Аналогичный

пример можно привести из области обоняния. Например, запах какого-

то блюда кажется вам немного подозрительным. Если вы заботитесь

о своем здоровье, вы не станете есть такое блюдо: лучше остаться

голодным (ошибка ложной тревоги), чем отравиться (ошибка

пропуска). Обратная тенденция будет наблюдаться, если цена ложной

тревоги высока. Например, влюбленный упорно не хочет замечать

недостатки характера предмета своего обожания, которые

очевидны для всех окружающих. Ведь в противном случае он рискует

потерять прекрасное чувство.

Другим понятием, связанным с проблемой порогов, является

дифференциальный порог, или порог различения.

Дифференциальный порог — это минимальное различие в интенсивности двух

раздражителей, при которой возникают отличные друг от друга

ощущения. Измерение дифференциального порога связано с

упомянутым уже нами эмпирическим фактом — нашей ограниченной

способностью к различению стимулов. Изучение

дифференциальных порогов оказывается очень важным для решения широкого

круга практических задач. Насколько автомобилист может превысить

допустимую скорость, чтобы его нарушение визуально не было

замечено регулировщиком движения? Не покажется ли вам, что

чемодан стал намного тяжелее, если положить в него еще одно платье?

Почувствуют ли гости, что блюдо пересолено, если хозяйка

положила в кастрюлю на 1 г больше соли, чем было указано в рецепте?

Ответ на эти вопросы дает психофизический закон Э. Вебера A795—

1878). Вебер поставил перед собой цель установить величину едва

заметного различия, т. е. наименьшего различия между двумя

физическими раздражителями, которое может определить человек. Он

экспериментировал со способностью различения веса. Оказалось,

что различительная способность зависит не от абсолютной, а от

относительной величины изменения. Так, испытуемому казались

разными грузы весом 40 г и 41 г, но грузы весом 80 г и 81 г оценивались

248 Глава 7 Познавательные процессы Ощущение и восприятие

как равные. Таким образом, Вебер установил, что величина едва

заметного различия составляет 1/40 от первоначального веса и

является константой. Одновременно с Вебером вел исследования и дру.

гой ученый — П. Бугер, поэтому этот психофизический закон

получил название по именам обоих авторов. Закон Вебера — Бугера

выражается формулой

AI/1= const. , где I — интенсивность стимула, Д/ — приращение

стимула.

Впоследствии были получены данные о величине едва

заметного различия относительно других модальностей (табл. 14)

Таблица 14

Дифференциальные пороги для ощущений различных модальностей

Вид ощущения

Ощущение изменения высоты звука 0,3

Ощущение изменения яркости света 1,7

Ощущение изменения веса предметов 2,5

Ощущение изменения громкости звука 1

Ощущения изменения давления на поверхность кожи 3,4

Ощущение изменения вкуса соляного раствора 20

Величина едва

заметного различия

(константа Вебера —

Бугера), %

Последующие исследования, правда, показали, что закон

Вебера — Бугера действителен только для средней части диапазона

чувствительности сенсорной системы. При приближении к пороговым

величинам в закон должна быть внесена поправка, отражающая

величину ощущения от деятельности самой системы (например,

биения сердца в слуховой модальности или собственного свечения

сетчатки в зрительной модальности).

Таким образом, в окончательном виде этот закон имеет

следующий вид. А//1′ + Р= const., где Р — поправка на «шум» от работы

сенсорной системы.

Эмпирический факт несовпадения объективной шкалы

изменения раздражителя и субъективной шкалы изменения ощущения был

описан основным психофизическим законом, установленным Фех-

нером и впоследствии модифицированным Стивенсом. Фехнер,

используя математические преобразования соотношения Вебера —

Бугера, пришел к выводу, что изменение силы ощущения

пропорционально десятичному логарифму изменения силы воздействующего

раздражителя. Другими словами, когда раздражитель растет в гео-

метрической прогрессии (увеличивается в N раз), ощущение

вырастает лишь в арифметической прогрессии (увеличивается на N).

Основной психофизический закон Фехнера выражается формулой

R = С (lg I — lg /о), где R — интенсивность ощущения, / —

интенсивность действующего стимула, /0 — интенсивность стимула,

соответствующая нижнему абсолютному порогу, а С — константа Вебе-

па — Бугера, специфичная для каждой модальности.

форма психофизической кривой для ощущения громкости

звука условно отражена на рис. 41.

Рис. 41. Логарифмическая кривая зависимости интенсивности

ощущения громкости от силы звука

При выведении этого закона Фехнер исходил из

невозможности непосредственной оценки испытуемым интенсивности

возникающего у него ощущения. Поэтому в его формуле единицами

измерения выступают физические величины. В 1941 г. С. Стивене из

Гарвардского университета выдвинул идею о возможности прямой

оценки человеком своих ощущений.

Х. Шиффман. Закон (отношение) Вебера. Закон Фехнера: Psychology OnLine.Net

Х. Шиффман. Закон (отношение) Вебера. Закон Фехнера
Добавлено Psychology OnLine.Net
1.03.2010 (Правка 1.03.2010)

Закон (отношение) Вебера

Изучение дифференциального порога занимает заметное место в истории измерения ощущений (психофизики). В 1834 г. Эрнст Вебер, немецкий психолог, изучал способность наблюдателей выполнять задания, связанные с необходимостью различать сигналы. Он определил, что количественные изменения сигнала — увеличение или уменьшение его интенсивности, необходимое для того, чтобы второй сигнал был воспринят как отличный от первого, — пропорциональны абсолютной величине сигнала. Иными словами, он заметил, что определение разницы между интенсивностями двух сигналов — вопрос скорее относительного восприятия, нежели абсолютного. Так, Вебер нашел, что добавление одной свечи к шестидесяти горящим свечам приводит к обнаруживаемому увеличению яркости, а добавление одной свечи к ста двадцати горящим свечам — нет. Для достижения ЕРР при ста двадцати свечах нужны как минимум две свечи. Продолжив разбирать этот пример, мы найдем, что для заметного увеличения освещенности при трехстах горящих свечах понадобятся пять или больше свечей, если горят шестьсот свечей — десять и т. д.

Следовательно, вывод, к которому Вебер пришел более ста пятидесяти лет тому назад, заключается в следующем: чтобы два сигнала — независимо от их абсолютной величины или интенсивности — можно было отличить друг от друга, разница между ними должна быть пропорциональна их абсолютной величине. Интуиция подсказывает, что этот общий принцип относительности сенсорного опыта — зависимость обнаружения разницы между сигналами от их абсолютной величины, действительно имеет смысл. Так, хотя две капли воды будут без труда обнаружены, если их добавят к содержимому маленькой пробирки, те же самые две капли, скорее всего, не вызовут никакого сенсорного эффекта, если их добавят к галлону воды. Точно так же мы легко обнаружим разницу между одним фунтом и двумя, но разницу между пятьюдесятью одним фунтом и пятьюдесятью двумя фунтами уловим с трудом, хотя разница между этими парами весов одна и та же — один фунт. Мы рассказали о фундаментальном принципе относительной сенситивности чувствительности), известном как закон, или отношение, Вебера, который(ое) выражается следующей формулой:

ΔI/I=k,

гдe I — интенсивность сигнала, соответствующая порогу чувствительности, ΔI — величина дифференциального порога, или инкремент интенсивности, который, будучи добавлен к интенсивности сигнала I, вызывает ЕРР (т. е. инкремент изменения чувствительности), и k — константа, зависящая от того, чувствительность такой сенсорной системы определяется.

Это уравнение свидетельствует о том, что отношение (k) минимально обнаруживаемого инкремента интенсивности (А/) (в бесконечном ряду разных значений интенсивности) к интенсивности исходного сигнала (I) постоянно. Следовательно, закон Вебера отражает соотношение, в соответствии с которым должна измениться интенсивность стимула, чтобы это изменение можно было обнаружить чтобы оно вызвало ЕРР), a k — константа для сигналов определенного рода, таких как яркость, громкость и вес. В примере с яркостью свечей значение дельта I для 60, 20, 300 и 600 зажженных свечей будет равно 1, 2, 5 и 10, и отношения Вебера будут соответственно равны 1/60, 2/120, 5/300 и 10/600, т. е. все они равны между собой и равны 1/60. Следовательно, в общем виде, определение значения k — это определение соотношения интенсивности сигналов, вызывающего ЕРР.

В табл. 2.8 представлены типичные отношения Вебера для разных сенсорных систем.

Таблица 2.8 Типичные отношения Вебера для разных сенсорных систем

Вкус (соль)	0,083
Яркость	0,079
Громкость	0,048
Вибрация (ощущаемая кончиками пальцев)	0,036
Длина линии	0,029
Тяжесть	0,020
Электрический ток	0,013

---

Примечание: для упрощения отношения Вебера выражаются десятичными дробями. Например, «тяжесть», 0,020, выраженная в виде отношения, равна 1/50 (или 2 %). Чем меньше отношение Вебера, тем меньше изменение интенсивности сигнала, воспринимаемое как ЕРР. Источник: Teghtsoonian (1971).

---

Обратите внимание на то, что отношение Вебера изменяется в широких пределах: для соленого вкуса оно высоко и равно 0,083 (8,3 %), а для электрического тока — всего лишь 0,013 (1,3 %). В случае ощущения веса отношение Вебера равно 0,02, или 2/100, а это значит, что для получения ЕРР необходимо увеличить исходный вес на 2 %. Следовательно, чтобы разница стала ощутимой, к стограммовому весу нужно добавить 2 г, к двухсотграммовому — 4 г, а к килограммовому — 20 г.

Величина отношения Вебера характеризует общую чувствительность данной сенсорной системы к сигналам разной интенсивности. Вспомните, что чем меньше отношение, тем меньше едва различимая разница между сигналами, следовательно, тем больше чувствительность к разнице в интенсивности сигналов. Данные, представленные в табл. 2.8, свидетельствуют о том, что люди менее чувствительны к разнице во вкусовых ощущениях и в освещенности (изменение — 8,3 % и 7,9 %) и наиболее чувствительны к разнице электрических разрядах и тяжести (изменение 1,3 % и 2 % соответственно).

Насколько точным показателем является отношение Вебера? Вообще оно достаточно валидно для сигналов, интенсивность которых варьирует в широких пределах, включая большинство из тех сигналов, с которыми мы сталкиваемся в повседневности, однако для очень слабых и очень интенсивных сигналов оно уже значительно менее валидно, и последнее утверждение справедливо для всех сенсорных систем. Мы полагаем, что в широком интервале средних значений интенсивности отношение Вебера является полезным критерием способности различать два сигнала. Однако оно имеет не только чисто прикладное значение; закон Вебера сыграл важную роль в измерении ощущений и является одним из самых широких эмпирических обобщений в истории экспериментальной психологии. Более того, он явился основой для количественной оценки связи между физическим раздражителем и сенсорным опытом (ощущением), и в первую очередь — для анализа, выполненного Г. Т. Фехнером.

Закон Фехнера

В 1860 г. Густав Теодор Фехнер опубликовал свой труд «Элементы психофизики» (G. N. Fechner, The Elements of Psychophysics) — работу, которой было суждено оказать огромное влияние на количественную оценку ощущений и восприятия. Основная мысль Фехнера заключалась в том, что между ментальным опытом — ощущением — и физическим раздражителем существует количественная связь. Он пытался вывести формулу, связывающую эти две величины, разработав численную шкалу ощущений, характеризующую данную сенсорную систему. Работа Фехнера завершилась созданием важного уравнения, отражающего зависимость интенсивности ощущения от величины физического сигнала. Он предположил, что дифференциальный порог (ΔI), вызывающий ЕРР, может быть использован в качестве стандартной единицы измерения для величины субъективного ощущения. (Вспомните, что дифференциальный порог характеризует дифференциальное изменение интенсивности раздражителя, соответствующее ЕРР.) Фехнер попытался создать шкалу, связывающую субъективный опыт — ощущения — (в единицах ЕРР) с изменениями интенсивности сигнала (в единицах ΔI). Он начал с предположения, что для данной сенсорной системы все ЕРР являются субъективно равными единицами ощущения. Это значит, что субъективные впечатления о разнице между двумя сигналами, отделенными друг от друга одной ЕРР, одинаковы для двух сигналов любой интенсивности. Следовательно, если взять два сигнала, расположенных на участке низкой интенсивности шкалы интенсивности и отделенных друг от друга одной ЕРР, ощущение разницы между ними будет точно таким же, как ощущение от разницы между двумя сигналами, расположенными на той же шкале на участке высокой интенсивности и тоже разделенными одной ЕРР. Иными словами, в соответствии с представлениями Фехнера каждая ЕРР независимо от места расположения на шкале интенсивности равна любой другой ЕРР.

Вспомните, что в соответствии с отношением Вебера данная ЕРР увеличивается пропорционально увеличению интенсивности сигнала (т. е. поскольку ΔI/I — константа, по мере увеличения I соответственно должна увеличиваться и ΔI). Это значит, что если базовая интенсивность низка, дифференциал, необходимый для того, чтобы возникла ЕРР, соответствует ей и тоже мал. Напротив, если начальная интенсивность высока, дифференциал, необходимый для возникновения ЕРР, относительно велик. Иными словами, в начале шкалы интенсивности два сигнала, разделенные одной ЕРР, будут располагаться рядом и их интенсивности будут различаться мало, в конце шкалы два сигнала, разделенные одной ЕРР, будут весьма существенно отличаться друг от друга по интенсивности. Эта взаимосвязь между ощущением и стимуляцией графически представлена на рис. 2.9.

Рис. 2.9. Связь между ощущением и стимуляцией, как ее трактует закон Фехнера Обратите внимание на то, что по мере увеличения интенсивности сигнала для того, чтобы разницы между единицами измерения ощущений (S) оставались равными, требуется все более значительная разница между единицами измерения интенсивности (I). Иными словами, в то время как ощущение увеличивается равномерно (в арифметической прогрессии), соответствующее увеличение интенсивности сигнала происходит физически неравномерно, но пропорционально (в геометрической прогрессии). Связь между величинами, одна из которых изменяется в арифметической прогрессии, а вторая — в геометрической, выражается логарифмической функцией. Следовательно, S = k logI. (Источник: J. P. Guilford, Psechometric Methods, New York: McGraw-Hill, 1954)

Если справедливо, что все ЕРР психологически равны, то из этого следует, что по мере равномерного увеличения шкалы ощущений (каждое последующее значение больше предыдущего на одну и ту же величину) расстояние между точками на шкале интенсивности сигнала увеличивается на неравные, но пропорциональные отрезки. Как следует из рис. 2.9, для получения соответствующего ощущения требуется все более и более интенсивный сигнал. Пользуясь количественными терминами, можно сказать, что в то время как количество единиц ощущения (т. е. ЕРР) возрастает в арифметической прогрессии (ордината), интенсивность сигналов возрастает в геометрической прогресии (абсцисса).

Связь между двумя переменными, одна из которых изменяется в арифметической прогрессии (ощущение), а вторая — в геометрической (интенсивность сигнала), выражается логарифмическим уравнением. Связь между ощущением, изменяющимся в арифметической прогрессии, и интенсивностью, изменяющейся в геометрической прогрессии, выражается логарифмическим уравнением, известным под названием закона Фехнера. Иными словами, величина ощущения является логарифмической функцией сигнала, или

S=klogI,

где S — величина ощущения, logI — логарифм физической интенсивности сигнала и k — константа, отражающая отношение Вебера для данного сенсорного параметра.

Эта логарифмическая зависимость показывает, что ощущение увеличивается медленнее, чем интенсивность сигнала; по мере увеличения интенсивности сигнала для достижения одного и того же сенсорного эффекта требуется все большая и большая его интенсивность. Иными словами, для достижения равных сенсорных эффектов требуются все более и более значительные увеличения интенсивности сигнала.

Насколько применим закон Фехнера для описания связи между ощущением и интенсивностью сигнала? Так же как и закон Вебера, на котором он основан, закон Фехнера достаточно надежен при многих условиях, но его действие ограничено, и он лучше всего служит для аппроксимации связи между величиной ощущения и интенсивностью сигнала. Основное допущение закона Фехнера о том, что все ЕРР равны, не бесспорно. Например, в соответствии с этим допущением звук, интенсивность которого на 20 ЕРР превышает абсолютный порог, должен быть в два раза громче того звука, интенсивность которого превышает звуковой порог на 10 ЕРР (ибо один содержит в два раза больше единиц ЕРР, чем другой). В действительности, однако, звук, интенсивность которого превышает порог на 20 ЕРР единиц, не в два раза, а гораздо громче того звука, интенсивность которого превышает порог на 10 ЕРР единиц. Следовательно, нельзя говорить о том, что эффект всех ЕРР для данного сенсорного параметра одинаков.

Некоторые мысли о Максе Вебере и социологии, свободной от ценностей | by ObjectPetitU

Может ли что-то действительно существовать вне системы ценностей? Можно ли быть «объективным» и полностью устранить «субъективность» в своих взглядах? В своем предыдущем посте я описал метод Верстехена, качественный подход в социальных науках к пониманию причин действий, подход, который Макс Вебер использовал в своей работе.

Продолжая тему написания о Максе Вебере, в этом посте я обсуждаю концепцию социологии без ценностей, мотивацию использования такого метода в историческом контексте для Макса Вебера, а также то, имеет ли этот подход какую-либо ценность. цена.

Почему свободная от ценностей социология важна для Макса Вебера?

Проще говоря, социология без ценностей определяется как исследователь, отбрасывающий свои собственные ценности и приближающийся к проблеме «без ценностей».

Прежде чем мы углубимся в детали определения и реальности бесценностного подхода, нам нужно понять, почему это произошло. Хотя Макс Вебер не был тем, кто выдвинул эту концепцию, очевидно, что он был тем, кто больше всего к ней привязался. [2]

По Веберу, социолога «

интересует то, что есть, а не то, что должно быть» [1]

Макс Вебер занимался исследованиями во времена потрясений, которые отражались в политике и просачивались во все ее учреждений, в том числе академических. Известно, что правительство различными способами вмешивалось в деятельность университетов. Лица, получающие докторскую степень, не получали докторскую степень из-за антисемитизма. Академикам, которых называли «приват-доцентами», платили в зависимости от количества учеников, посетивших их лекции. Из-за этого некоторые лекторы также были более популярны, чем другие, например, те, кто был антисемитом и поддерживал Бисмарка[1]. Для Вебера это представляло проблему. С его общей целью разработать современные рациональные методы’ в Германии, для преодоления этих проблем он считал следующее:

1. Государство не должно вмешиваться в университеты.
2. Лекторы должны проявлять сдержанность в продвижении своих ценностей.

Вебер считал, что, ограничивая государственное вмешательство, а также продвигая личные ценности, люди могут использовать рациональные научные методы для решения проблем.

ПРИМЕЧАНИЕ. Общая тема, разработанная в Allen et al. , заключается в том, что Вебер хотел, чтобы Германия стала колониальной сверхдержавой, и для достижения этого использовались современные научные методы. В то время другие европейские страны были на пути к [1] ​​

Немецкая колониальная империя

Принимая во внимание вышеизложенное Вебера, становится понятно, к чему он стремится. Он видит проблему и хочет ее преодолеть, но жизнеспособно ли решение? Во-первых, процесс социального исследования требует изучения определенной темы. Затем, в рамках этой темы, исследователь может взять из этой темы то, что он считает ценным, что он считает достойным дальнейшего разъяснения. То, что они считают ценным, исходит из их собственной системы ценностей, поэтому мы видим, что ничто не может быть полностью «объективным». Вебер пытается разделить идеи:

1. Свобода ценностей: Отложите в сторону все оценочные суждения, когда будете участвовать в процессе анализа.
2. Актуальность ценности: Исследователь выбирает конкретные проблемы для решения на основе своей собственной системы ценностей.

Мы можем видеть это в собственной работе Вебера, Протестантская этика. Проблема «Как зародился западный капитализм?» рассматривалась через призму его происхождения, протестантизма.

Здесь нужно сделать несколько замечаний:

1. Таким образом, принимая во внимание понятие релевантности ценностей, он заключает, что рациональные подходы нежизнеспособны/невозможны, и, следовательно, никакой критики быть не может.
2. Таким образом, ученые могут выбирать проблемы на основе своей системы ценностей, но только один раз. ведется расследование, им необходимо отказаться от своих собственных убеждений.[1]

К первому пункту: Это несколько опасно. Учитывая концепцию значимости ценности, поскольку мы допускаем некоторые личные предубеждения, наша критика не имеет ценности. Подход, который предполагает, что из-за этого ограничения никакая критика не допускается, заключается в том, чтобы обеспечить сохранение статус-кво, каким бы он ни был. Если нет критики, может ли быть прогресс? Если вы не можете критиковать, как могут произойти изменения? Вопрос, который имеет непосредственное отношение (который мы не будем здесь обсуждать) к этому, заключается в том, кто устанавливает стандарты для текущего режима работы? И не перестанут ли люди вдруг формировать мнение/Критику?

Я думаю, что интересным отражением этого является нынешнее время, в котором мы живем. Культура «пробуждения» — это то, что преобладает, «культура отмены», люди отменяются, потому что они придерживаются определенного мнения. В этих сценариях аргумент заключается в политике идентичности и в том, что людям не разрешается/проецировать определенное мнение, потому что оно оскорбляет других.

Причина, по которой я поднимаю этот вопрос, потому что проснувшаяся культура кажется интересной. Это некая форма, инверсия мышления Вебера. Проснувшаяся культура также «отменяет» научные открытия. Дело не в том, что оно ограничено мнениями или социальным порядком. Если научные открытия представляют что-то «гнетущее», то ими также пренебрегают.

Учитывая, что мы живем в постпросвещенном мире, Вебер кажется более разумным, чем культура «пробуждение/отмена». Учитывая, что Просвещение поддерживало подход научного мышления, наблюдения, эмпиризма, мы видим здесь, что, возможно, мир видит его пределы. Если мы живем в обществе, которое не является христианским одиночкой или находится в тени христианства, и все мы живем со светским мышлением, тогда, конечно, идея Вебера имеет какой-то смысл? Я думаю, что в достижении этой точки есть логика, однако, если мы заглянем немного глубже, я думаю, мы найдем кое-что еще.

Ко второму пункту: Что значит отказаться от своих убеждений? Значит ли это, что мы ни во что не верим? Означает ли это, что мы также отказываемся от нашей веры в науку? Я думаю, что здесь имеет место парадокс.

Наука — это метод (множество аргументов по определению науки, которые мы оставим для следующего поста). Есть так много вещей, которые существуют в реальности, в обществе, которых мы знаем внутри себя, которые не могут поддаться эмпирической форме. На самом деле это довольно забавно, потому что социология, социальные науки, являются предметами, которые заполнены больше, чем другие области изучения, в которых мы знаем, что происходят вещи, которые нам трудно эмпирически доказать, или мы можем доказать, но только на определенных уровнях (например, коллективно). ).

Если мы сможем анализировать эмпирические данные, то даже подход к анализу может измениться. Разве это не включает систему убеждений? У всех нас есть подходы при проведении определенного анализа, на самом деле, во многих ситуациях может быть более одного «научного» подхода к проведению анализа. Во-вторых, если существует более одного подхода и использование более чем одного дает разные ответы, мы исследуем несоответствие.

Заключительные замечания

Бесценностная социология в мысли Вебера — интересная концепция. Идея свободы ценностей и значимости ценностей имеет большой смысл, но, безусловно, сдерживание критики или научного процесса из-за релевантности ценностей кажется несколько недальновидным.

Достаточно сказать, что идея Вебера просто непрактична, и, что наиболее важно, он сам становится ее жертвой (что мы МНОГО видим в работах Вебера).

Думая об этом шире, придание слишком большой силы научному методу означает, что мы всегда находимся в подвешенном состоянии, мы всегда узнаем. Я думаю, что использование научного метода великолепна, и мы смогли так много продвинуться в науках, но как насчет обычных людей? Они движутся с наукой? Можем ли мы идти в ногу с его прогрессом? Менять нашу жизнь каждые несколько лет. Думаю, нет. Я думаю, что для большинства из нас мы знаем некоторые вещи, мы растем определенным образом, мы принимаем некоторые идеалы, но постоянное изменение нашего мировоззрения было бы чрезвычайно утомительно.

Я, конечно, еще не все понял. Эта статья представляет собой исследование некоторых идей, о которых я думаю, и их отношения к миру, в котором я живу.

Библиография

[1]: Аллен, К. (2004). Макс Вебер: критическое введение . ЛОНДОН; ЭНН-АРБОР, Мичиган: Pluto Press. Получено с www.jstor.org/stable/j.ctt18fs592

[2]: МАКС ВЕБЕР И ПРОИСХОЖДЕНИЕ ИДЕИ СОЦИАЛЬНОЙ НАУКИ, БЕЗ ЦЕННОСТЕЙ. АЛЛАН Н. ШАРЛИН. Европейский журнал социологии. Том. 15, №2, с. 337–353

Макс Вебер – Грэм Скамблер

Макса Вебера долгое время называли «социологом социолога», главным образом в знак признания не только широкого охвата его научных исследований и его общего анализа общественного развития и изменений, а также конкретных существенных вопросов, но его работы по философии и методам исследования. Однажды я выступал в Мюнхене прямо под бюстом Вебера и был должным образом запуган.

Он считается «методологическим индивидуалистом». Это отличает его как от Маркса, так и от Дюркгейма, которые оба, хотя и по-разному, рассматривают такие понятия, как социальный класс и органическая солидарность, как несущие смысл за пределами мыслей и действий тех индивидуумов, которых они включают. Для Вебера подобные понятия имеют смысл только в том случае, если они могут быть укоренены в том, что люди думают и делают, и порождены ими.

Давайте немного остановимся на философии и методах. Одно различие, которое сделал Вебер, касалось «отсылки к ценности» и «оценочного суждения». Первый признает, что социологи — неизбежно и неизбежно — принимают решения о том, что исследовать: решить исследовать один вопрос — значит признать его личную значимость, а также отвергнуть конкурирующие возможности. В этом смысле исследовательские проекты отражают личные ценности исследователей, а также, во все большей степени, источников институционального финансирования. Мы должны относиться к этому рефлексивно. Однако, выбрав область, явление или тему, крайне важно, чтобы социологи избегали оценочных суждений, то есть вторжения в проведение своих исследований личных или институциональных «предубеждений». В этом смысле исследования должны быть нейтральными по отношению к ценностям.

Вебер мог многое сказать о методологии. Он был сосредоточен на причинном объяснении. Его приверженность заключалась в «интерпретации действия в его субъективном значении». От имени социологии он искал объективную оценку субъективных миров . Жизненно важным компонентом социологического исследования, утверждал он, является verstehen , или эмпатическое понимание: важно, чтобы исследователи ставили себя на роли и «головы» других. Одним из средств достижения этой цели было его понятие «идеальных типов». Они развернуты, чтобы предложить логически и формально точные утверждения о возможных причинно-следственных связях. Классический пример — выдвинутая им гипотеза о причинно-следственной связи между «протестантской этикой» и «духом капитализма». Что значит «быть кальвинистом» и «быть капиталистом»? Вебер сконструировал идеальные типы протестантской этики и духа капитализма (что он имел в виду), а затем приступил к эмпирическому исследованию, чтобы увидеть, ведет ли первое ко второму. Важно отметить, что идеальные типы определяют, что социологи «подразумевают под ними»; они не должны иметь эмпирических референтов, т. е. отражать реально существующие положения дел. Вывод Вебера в этом конкретном исследовании часто понимают неправильно. Он нашел «избирательную близость» между протестантской этикой и духом капитализма. Он сделал , а не утверждают, что протестантская этика привела к взлету капитализма на Западе, то есть что идеи превзошли материальные условия (Маркса). Скорее он утверждал, что отколовшийся кальвинистский акцент на доктрине предопределения (чье-то спасение или иное было «предопределено») косвенно привел к мнению, что духовное предназначение человека подразумевается «его» материальными обстоятельствами: другими словами, накопление капитала и отказ от гедонизма указывали на спасение. Для ясности: Вебер утверждал, что структурные/материальные обстоятельства появления капитализма существовали до его появления на Западе (например, в Китае)9.0013, но именно протестантизм/кальванизм послужил «спусковым крючком» для преобразования структурных/материальных обстоятельств в новую экономическую систему и новую эпоху. В этом смысле капитализм был непреднамеренным следствием протестантской этики. Идеи не обязательно должны быть каузально определяющими, чтобы быть каузально релевантными. Вебер дополнил и исправил, а не вытеснил марксова трактовка истоков капитализма.

При этом ориентация Вебера на социальную стратификацию отличалась от ориентации Маркса. Он не столько оторвался от последней концепции класса, сколько переосмыслил ее. Для Вебера существует три измерения стратификации: класс, конечно, но также статус/честь и партия (или политическая организация/принадлежность). В то время как статус и партия, как правило, следуют классу, они не обязательно делают это и иногда расходятся . Короче говоря, социальная стратификация многомерна, более сложна и менее социологически прямолинейна, чем утверждал Маркс.

В основе большей части социологии Вебера лежит понятие «рационализации». Он утверждал, что современные, западные, сложные и сильно дифференцированные общества свидетельствуют о распространении одной из различных форм власти. Он различал три типа «авторитета». Он упомянул, во-первых, инструментальную рационализацию или рационализацию средств и целей. Деннис Вронг пишет:

, под «рационализацией» Вебер понимал процесс, посредством которого явные, абстрактные, интеллектуально исчисляемые правила и процедуры все больше заменяют чувства, традиции и эмпирические правила во всех сферах деятельности. Рационализация ведет к вытеснению специальной наукой основного источника интеллектуального авторитета; замена культурного литератора обученным специалистом; вытеснение квалифицированного ручного труда машинной технологией; замена судебной мудрости абстрактными, систематизированными сводами законов. Рационализация демистифицирует и инструментализирует жизнь. Это означает, что… нет никаких таинственных, неисчислимых сил, которые вступают в игру, а скорее, что можно, в принципе, управлять всем с помощью расчета. Это означает, что мир расколдован. (курсив мой). ’

Вебер противопоставляет: (а) традиционный авторитет и (б) харизматическую рациональность неумолимому подъему этой инструментальной или средств-целей рациональности. Первый обозначает в значительной степени досовременную форму власти, хотя и сохранившуюся до настоящего времени, в то время как последний признает и в конечном итоге верит в появление личностей с жизненно важным, нестандартным (таким образом, «харизматичным») обращаться. Гитлер, к сожалению, является наиболее очевидным кандидатом, равно как и Трамп и, что ближе к дому, популист и преуспевающий бывший брокер UKIP Фарадж. Итак, намекает Вебер, харизма может, и, может быть, это и есть оптимальная ставка на будущее, вывести людей из железной клетки.          

Обнажая незапланированное вмешательство харизматической личности, в благоприятных социально-экономических и социально-политических эффективные расчеты и практика, воплощенные в науках. Он утверждал, что это функция возникновения современных, сложных, высокодифференцированных обществ, будь то капиталистические или иные (например, коммунистические). Будущее бюрократично.

 

Вот так:

Нравится Загрузка. ..

Внутреннее значение Weber: DCF (на основе FCF) | WEBR

: -41,64 доллара США (на сегодняшний день)

Просмотрите и экспортируйте эти данные начиная с 2021 года. Начните бесплатную пробную версию

Модель денежного потока: $-41,64 .

Примечание. Модель дисконтированных денежных потоков подходит только для предсказуемых компаний (рейтинг предсказуемости бизнеса выше 1 звезды). Если рейтинг предсказуемости компании равен 1 звезде или рейтингу нет, результат может быть неточным из-за низкой предсказуемости бизнеса, и данные не будут храниться в нашей базе данных.

Ранг Вебера по предсказуемости: Без рейтинга . Таким образом, эта страница используется только в демонстрационных целях, и результаты, связанные с DCF, в скринере и портфолио будут отображаться как нулевые.

Запас прочности (на основе FCF) с использованием модели дисконтированных денежных потоков для Weber составляет Н/Д.

Отраслевой рейтинг внутренней стоимости Weber: DCF (на основе FCF) или связанный с ним термин показан ниже:

---

Внутренняя стоимость Weber: DCF (на основе FCF) Исторические данные

Тенденция исторических данных для внутренней стоимости Weber: DCF ( На основе FCF) можно увидеть ниже:

* Для раздела «Операционные данные»: все числа указаны единицами измерения после каждого термина, а все суммы, связанные с валютой, указаны в долларах США.
* Для других разделов: Все числа указаны в миллионах, за исключением данных на акцию, коэффициента и процента. Все суммы, связанные с валютой, указаны в соответствующей валюте фондовой биржи компании.

* Только премиум-члены.

Ежегодные данные Weber
	Тренд	Сентябрь 18	Сентябрь 19	20 сентября	21 сентября
Внутренняя стоимость: DCF (на основе FCF)		—	—	—	—

Ежеквартальные данные Weber
	Сентябрь 18	Сентябрь 19	20 марта	20 июня	20 сентября	20 декабря	21 марта	21 июня	21 сентября	21 декабря	22 марта	22 июня
Внутренняя стоимость: DCF (на основе FCF)								—	—	—	—	—

---

Weber Внутренняя стоимость: расчет DCF (на основе FCF)

Это внутренняя стоимость, рассчитанная на основе модели дисконтированных денежных потоков с параметрами по умолчанию. В модели дисконтированных денежных потоков будущий денежный поток оценивается на основе темпа роста денежного потока и ставки дисконтирования. Денежный поток будущего дисконтируется до его текущей стоимости по ставке дисконтирования. Все дисконтированные будущие денежные потоки суммируются, чтобы получить текущую внутреннюю стоимость компании.

Обычно двухэтапная модель используется при расчете внутренней стоимости акций с использованием модели дисконтированных денежных потоков. Первая стадия называется стадией роста; вторая называется терминальной стадией. На стадии роста компания растет более быстрыми темпами. Поскольку он не может расти с такой скоростью вечно, для терминальной стадии используется более низкая скорость.

Калькулятор GuruFocus DCF представляет собой двухступенчатую модель. Значения по умолчанию определены следующим образом:

1. Ставка дисконтирования: d = 10%
Разумное допущение в отношении ставки дисконтирования должно быть, по крайней мере, долгосрочной средней доходностью фондового рынка, которая может быть оценена на основе безрисковой ставки плюс премия за риск в размере фондовый рынок.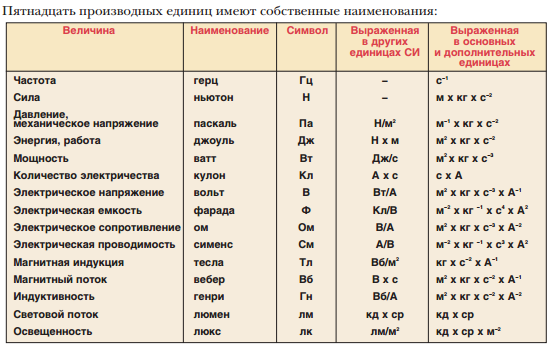 Мы использовали 10-летнюю постоянную ставку погашения казначейских облигаций в качестве безрисковой ставки и округлили до ближайшего целого числа, а затем добавили премию за риск в размере 6%, чтобы получить расчетную ставку дисконтирования. Некоторые инвесторы используют ожидаемую норму прибыли, что также разумно. Типичная ставка дисконтирования может составлять от 6% до 20%.

2. Темп роста на стадии роста: g1 = 5%
Темп роста на стадии роста = средний темп роста свободного денежного потока за последние 10 лет. Если он выше 20%, мы используем 20%. Если он меньше 5%, вместо этого мы используем 5%. => Для компаний со средним темпом роста свободного денежного потока за последние 10 лет менее 5% GuruFocus по умолчанию => Темп роста: 5%

3. Годы стадии роста: y1 = 10

4. Скорость конечного роста: g2 = 4%

5. Годы конечного роста: y2 = 10

6. Свободный денежный поток на акцию: fcf = -3,335 доллара США.
Однако калькулятор GuruFocus DCF на самом деле является калькулятором дисконтированных доходов, по умолчанию используется EPS без NRI. Причина, по которой мы это делаем, заключается в том, что мы обнаружили, что исторически цены на акции больше коррелируют с прибылью, чем со свободным денежным потоком.

Все настройки по умолчанию можно изменить, и результаты рассчитываются автоматически.

Внутренняя стоимость Weber: DCF (на основе FCF) для сегодня рассчитывается как 910) / (1-й)] = -3,335 * 12,485 = -41,64

Маржа безопасности (на основе FCF)	=	(внутреннее значение: DCF (FCF)	—	.
	=	(-41,64	—	6,47)	/	-41,64
	=	Н/Д

* Для раздела «Операционные данные»: все числа указаны в единицах измерения после каждого термина, а все суммы, связанные с валютой, указаны в долларах США.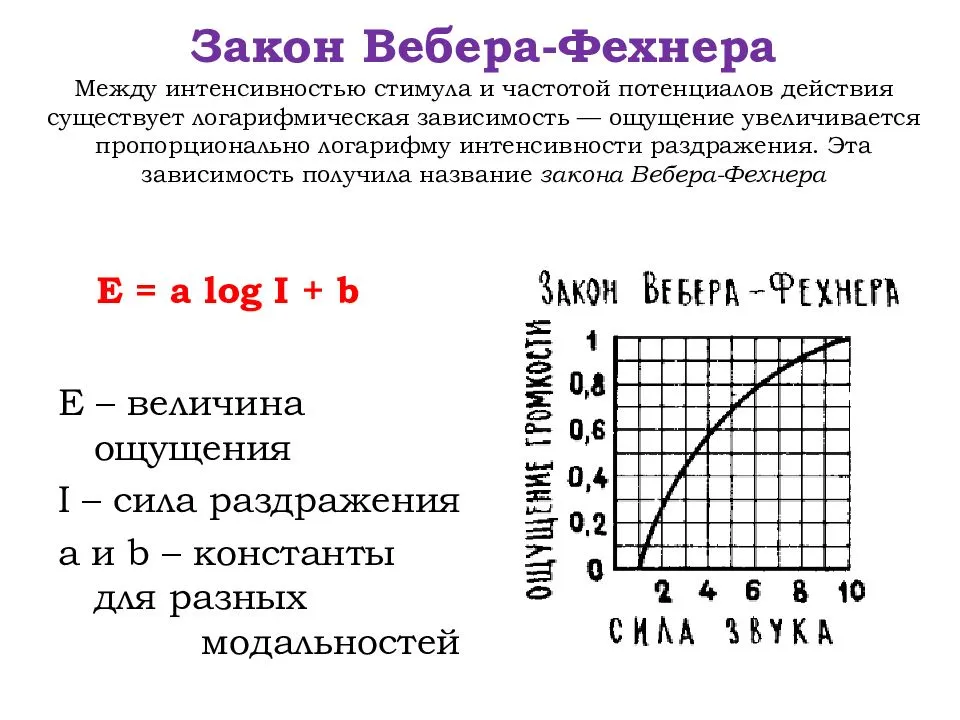
* Для других разделов: Все числа указаны в миллионах, за исключением данных на акцию, коэффициента и процента. Все суммы, связанные с валютой, указаны в соответствующей валюте фондовой биржи компании.

---

Weber  (NYSE:WEBR) Внутренняя стоимость: DCF (на основе FCF) Объяснение

В отличие от таких методов оценки, как стоимость чистых текущих активов, материальная балансовая стоимость на акцию, число Грэма, медианная стоимость PS и т. д., модель дисконтированных денежных потоков оценивает компании на основе их будущей доходной способности, а не их активов.

---

Будьте в курсе

Что нужно знать о модели DCF:

1. Модель DCF оценивает компанию на основе ее будущей прибыли
2. Учитывается рост; поэтому быстрорастущая компания стоит больше, если все остальное остается прежним.
3. Поскольку мы прогнозируем будущий рост, предполагается, что компания будет расти такими же темпами, как и в течение последних 10 лет. Поэтому эта модель лучше работает для компаний с относительно стабильной производительностью.
4. Модель DCF плохо работает для непостоянных исполнителей, таких как циклические акции.
5. Какую ставку дисконтирования следует использовать? Ваш ожидаемый доход от инвестиций является хорошим предположением о ставке дисконтирования.
6. Больший запас прочности должен требоваться для компаний с менее предсказуемым бизнесом.

С помощью многофункционального скринера GuruFocus вы можете отслеживать акции, торгующиеся ниже их внутренней стоимости: DCF (на основе FCF) и внутренней стоимости: DCF (на основе доходов). Компании с высоким рейтингом предсказуемости, которые торгуются со скидкой к их внутренней стоимости: DCF (на основе FCF) и внутренней стоимости: DCF (на основе прибыли), можно найти на экране недооцененных предсказуемых компаний.

---

Внутренняя стоимость Weber: DCF (на основе FCF) Связанные термины

Благодарим вас за просмотр подробного обзора внутренней стоимости Weber: DCF (на основе FCF), предоставленного GuruFocus.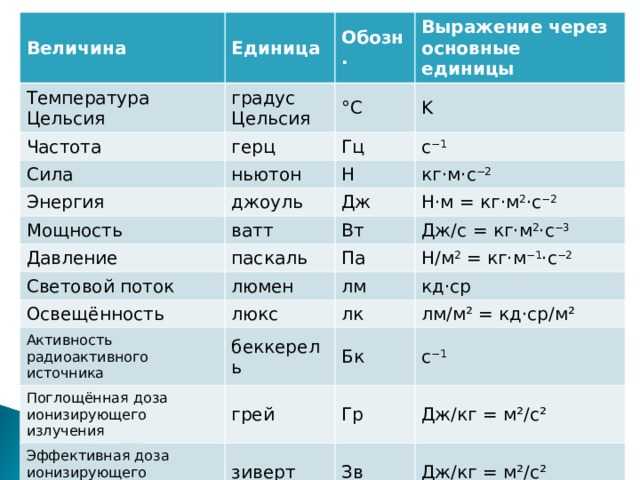 com. Пожалуйста, нажмите на следующие ссылки, чтобы увидеть соответствующие страницы терминов.

---

Описание деятельности Weber

Сопоставимые компании

NAS:PRPL НАС:КБАЛ НАС:ЛЮБОВЬ NAS: LCUT NYSE:КУК NAS:ATER NAS:ХОФТ Нью-йоркская фондовая биржа: ETD NAS:BSET Нью-йоркская фондовая биржа: HBB СЗСЕ: 000333 ШСЭ: 600690 СЗСЕ: 000651 ШСЭ: 603833 Нью-Йоркская фондовая биржа:WHR Нью-йоркская фондовая биржа: FBHS Нью-йоркская фондовая биржа: МХК ШСЭ: 603486 СЗСЕ: 002032 SHSE:605117

Торгуется на других биржах

N/A

Адрес

1415 S. Roselle Road, Palatine, IL, USA, 60067

3 9006 Веб-сайт0066

https://www.weber.com

Weber Inc — компания, занимающаяся приготовлением пищи на открытом воздухе, предлагает разнообразный портфель продуктов, включающий типы топлива, ценовые категории, а также широкий спектр аксессуаров, расходных материалов и услуг. Он получает доход от продажи грилей и сопутствующих аксессуаров.

Руководители

Сотрудник Сотрудник Сотрудник

Уоррен Бо	: Президент, Weber Americas	1415 S. ROSELLE ROAD ПАЛАТИН IL 60067
Хан Штеффен	сотрудник: Президент, Weber EMEA	1415 S. ROSELLE ROAD ПАЛАТИН IL 60067
Тротт Байрон Д	директор, 10-процентный владелец	71 SOUTH WACKER DRIVE, 12 ЭТАЖ ЧИКАГО IL 60606
БДТ Капитал Партнерс, ООО	директор, 10-процентный владелец	401 NORTH MICHIGAN AVENUE SUITE 3100 CHICAGO IL 60611
Бдтцп Гп И, ООО	директор, 10% владелец	401 NORTH MICHIGAN AVENUE SUITE 3100 CHICAGO IL 60611
БДТП ГП, ООО	директор, 10-процентный владелец	401 NORTH MICHIGAN AVENUE SUITE 3100 CHICAGO IL 60611
Bdt Capital Partners I-a Holdings, Llc	директор, 10-процентный владелец	C/O BDT CAPITAL PARTNERS 401 NORTH MICHIGAN AVENUE, SUITE 3100 CHICAGO IL 60611
Wsp Investment LLC	10-процентный владелец	14 СЕВЕРНАЯ ПЕОРИЯ СТРИТ, НОМЕР 2E ЧИКАГО IL 60607
Бдт Всп Холдингс, ООО	директор, 10-процентный владелец	C/O BDT CAPITAL PARTNERS 401 NORTH MICHIGAN AVENUE, SUITE 3100 CHICAGO IL 60611
Mad Private Family Trust Co Ltd	10-процентный владелец	8805 TAMIAMI TRAIL N STE 356 NAPLES FL 34108
Weber-stephen Management Pool LLC	10-процентный владелец	C/O BDT CAPITAL PARTNERS 401 NORTH MICHIGAN AVENUE, SUITE 3100 CHICAGO IL 60611
Маккорт Мартин	директор	1415 С. РОЗЕЛЬ РОУД ПАЛАТИН, Иллинойс 60067
Стивен Джеймс К.	директор	1415 S. ROSELLE ROAD ПАЛАТИН IL 60067
Килпатрик Марла Ивонн	: глобальный контролер и CAO	1415 S. ROSELLE ROAD ПАЛАТИН IL 60067
Сагрипанти Мэри А.	: Директор по маркетингу	1415 С. РОЗЕЛЬ РОУД ПАЛАТИН, Иллинойс 60067

---

Weber Headlines

От GuruFocus

Bdt Capital Partners, Llc покупает Weber Inc, Krispy Kreme Inc, продает Keurig Dr Pepper Inc

Инсайдер 16.11.2021

Weber Inc. запускает 1952 Ventures LLC и объявляет о назначениях и продвижении по службе высшего руководства

По деловой проводке 18.11.2021

Weber объявляет ежеквартальные денежные дивиденды

По деловой проводке 03. 11.2021

Weber Inc. преобразует приготовление пищи на открытом воздухе с помощью инновационного портфолио продуктов 2022 года

По деловой проводке 18.01.2022

Weber Inc. представляет новую лимитированную коллекцию чайников в ознаменование 70-летия оригинального чайника Weber

По деловой проводке 24-02-2022

Weber Inc. официально открывает свой новый европейский производственно-дистрибьюторский центр

По деловой проводке 07.10.2021

Weber объявляет ежеквартальные денежные дивиденды

По деловой проводке 03-02-2022

Weber Inc. объявит результаты за третий финансовый квартал 2021 года 15 сентября 2021 года

По деловой проводке 09-08-2021

Weber Inc. объявит результаты за четвертый финансовый квартал и 2021 год за весь 2021 год 8 декабря 2021 года

По деловой проводке 01.12.2021

Weber Inc. объявит финансовые результаты за первый квартал 2022 финансового года 14 февраля 2022 г.

По деловой проводке 02-04-2022

Другие источники

$WEBR — Weber сообщил о сильном квартальном импульсе и выглядит недооцененным. Сильный квартальный импульс Weber кажется недооцененным

By Seekingalpha 2022-02-19

Стоит ли вам делать ставку на приготовление гриля на открытом воздухе?

Дурак 2021-09-14

Является ли Weber Stock хорошей покупкой для долгосрочных инвесторов?

Дурак 2021-12-11

$WEBR — Генеральный директор Weber Inc. (WEBR) Крис Шерзингер о результатах за четвертый квартал 2021 года — расшифровка отчета о доходах.…

By Seekingalpha 2021-12-08

$WEBR — Weber: Приносим тепло на улицу. Weber Webr приносит тепло на улицу

By Seekingalpha 2021-10-21

$WEBR — Генеральный директор Weber Inc. (WEBR) Крис Шерзингер о результатах за третий квартал 2021 года — стенограмма телефонного разговора о доходах.…

By Seekingalpha 2021-09-15

Вебер сообщает о плохих результатах первого квартала; Промахи оценки

Автор: tipranks. com 15 февраля 2022 г.

$WEBR — Если мне нужно купить одного игрока на рынке кулинарии на открытом воздухе, это Weber Inc. — Вот почему.…

By Seekingalpha 2021-12-30

$WEBR — Генеральный директор Weber Inc. (WEBR) Крис Шерзингер о результатах за четвертый квартал 2021 года — стенограмма телефонного разговора о доходах.…

By Seekingalpha 2021-12-08

Временная основа закона Вебера при восприятии ценности (Dehaene and Brannon, 2011; Droit-Volet, 2013; Akre and Johnsen, 2014), яркость (Rovamo et al., 19).95), количество (Whalen et al., 1999; Cordes et al., 2001; Nieder and Miller, 2003; Cantlon and Brannon, 2006; Beran, 2007; Gallistel, 2011; Droit-Volet, 2013), величина вознаграждения (Killeen et al., 1993; Bateson et al., 1995; Kacelnik and Bateson, 1996), время (Gibbon, 1977; Gibbon et al., 1984; Matell and Meck, 2000; Buhusi and Meck, 2005), громкость (Forrest, 1994; Bee et al., 2012) и др. (Akre and Johnsen, 2014). Он утверждает, что способность воспринимать изменение количества уменьшается пропорционально его величине.

Тот факт, что наша способность воспринимать изменение раздражителя часто уменьшается по мере увеличения его величины, становится очевидным; например, труднее ощутить увеличение на 1 г при измерении 100 г, а не при измерении 2 г. Закон Вебера, однако, гласит, что это снижение способности оценивать величину пропорционально величине стимула, т. е. что воспринять данное изменение в пределах 100 g в 50 раз труднее, чем воспринять такое же изменение в пределах 2 грамм. Несмотря на значительное экспериментальное подтверждение этого закона, его нервное или эволюционное происхождение неясно (Walsh, 2003; Bueti and Walsh, 2009).; Акре и Йонсен, 2014). Кроме того, поскольку часто считается, что животные принимают решения, чтобы максимизировать уровень вознаграждения (что требует восприятия величины вознаграждения и задержки) (Stephens and Krebs, 1986; Balci et al., 2011; Blanchard et al., 2013; Namboodiri et al. ., 2014b), закон Вебера в восприятии величины вознаграждения и задержки должен влиять на такие решения. Однако математические свойства такого воздействия на решения животных неясны.

Ранее мы представили теорию принятия решений и восприятия времени, которая постулирует, что решение животных относительно отсроченных результатов является следствием максимизации уровня вознаграждения в ограниченном временном окне, включающем прошлый интервал интеграции (в течение которого опытная норма вознаграждения оценивается) и задержкой данного вознаграждения (TIMERR) (Namboodiri et al., 2014b). Мы показали, что алгоритм принятия решений, вытекающий из этого постулата, автоматически включает оценку альтернативной стоимости и явную стоимость времени. Далее мы показали, что это может объяснить широту поведенческих наблюдений за межвременным принятием решений. Теория также постулирует, что время представлено субъективно таким образом, что субъективная ставка вознаграждения равна объективному изменению ставки вознаграждения, т. е. оценка субъектом субъективной ценности в единицу субъективного времени точно представляет, насколько ставка вознаграждения за текущее предложение превышает пережитое. ставка вознаграждения. Используя эту теорию, мы исследуем происхождение закона Вебера в отношении величины вознаграждения в этой статье и показываем, что восприятие величины вознаграждения коррелирует с восприятием времени и что субъективное изменение ценности отсроченного вознаграждения также должно приблизительно подчиняться закону Вебера. . Мы также представляем новую накопительную модель сенсорного восприятия, которая предсказывает приблизительный закон Вебера для величин (таких как величина вознаграждения), которые измеряются в течение конечных сенсорных интервалов.

Результаты

Наша главная цель в этой статье — изучить, как ошибки в субъективном представлении интервала соответственно влияют на субъективную ценность этого вознаграждения. С этой целью мы сначала выразим субъективную ценность отсроченного вознаграждения в терминах субъективного представления об отсрочке.

Субъективная ценность вознаграждения величиной r , отложенная на интервал t , рассчитанная в TIMERR (рис. 1), составляет:

SV(r,t)=r−aestt1+tTime    (1)

, где T _ime представляет прошлый интервал интегрирования, т. е. интервал, в течение которого оценивается прошлый коэффициент вознаграждения ( a _est ). Важно отметить, что T _ime — это не воспринимаемый временной интервал, а просто эффективный интервал, в течение которого оценивается прошлый уровень вознаграждения (например, с использованием экспоненциального фильтра памяти, как в Namboodiri et al., 2014a).

Рисунок 1. Субъективная ценность отсроченного вознаграждения ( r ) рассчитывается как немедленное вознаграждение, которое дает одинаковую общую ставку вознаграждения за окно, включая интервал прошлой интеграции ( T _ime ) (по которому рассчитывается опытная ставка вознаграждения, a _est ) и ожидаемая задержка ( t ) до будущего вознаграждения . На рисунке показано готовое средство для визуального отображения субъективной ценности отсроченного вознаграждения, показанное фиолетовой полосой в нулевое время («сейчас»). Изменено из Namboodiri et al. (2014а).

В приведенном выше уравнении r можно рассматривать как величину предлагаемого вознаграждения. Но более строгое определение 90 846 r 90 847 — это субъективная ценность немедленно предложенного вознаграждения, т. е. 90 846 r 90 847 = 90 846 SV 90 847 (90 846 r 90 847, 0).

Соответственно, субъективное представление задержки t , выраженное в TIMERR, равно:

ST(t)=t1+tTime    (2)

-линейность контролируется прошлым интервалом интегрирования. Важно подчеркнуть, что субъективное представление о задержке, выраженное выше, не является субъективным (вербальным) отчетом об интервале; его можно рассматривать как нелинейное нейронное представление интервала.

Уравнение (1) теперь можно переформулировать в терминах субъективного представления времени, как показано в уравнении (2), как

SV(r,t)=r1+tTime-aestST(t)=rST(t) t−aestST(t)             =rST(t)ST(t)1−ST(t)Time-aestST(t)    (3)

Следовательно,

SV(r,t)=r−(rTime+aest) ST(t)    (4)

Таким образом, дисконтирование отложенного вознаграждения является линейным по отношению к субъективному представлению об этой задержке. Здесь мы предполагаем, что субъективная ценность отсроченного вознаграждения рассчитывается путем сначала измерения субъективного представления о задержке, а затем линейного дисконтирования с использованием формы, выраженной в уравнении (4). Это линейное дисконтирование по отношению к субъективному представлению о времени является прямым результатом постулата нашей теории о том, что животные максимизируют уровень вознаграждения в течение ограниченного временного окна, включая прошлый интервал интеграции и задержку будущего вознаграждения.

Вклад ошибки измерения времени в ошибку субъективной оценки

Теперь из этого соотношения мы можем рассчитать ошибку субъективной ценности отсроченного вознаграждения в результате ошибки в представлении субъективного времени (рис. 2). С этой целью обозначим, что едва заметное различие (JND) в субъективном представлении ST(t) задержки t на δ ST(t) , и что ошибка в соответствующем субъективном представлении значение обозначается δ СВ ( р, т ). Для целей этого раздела мы предполагаем, что измерение величины вознаграждения бесшумно. Затем, когда субъективное представление задержки t увеличивается на ее JND, субъективное значение будет увеличиваться на соответствующую ошибку. Математически это можно выразить следующим образом:

SV(r,t)+δSV(r,t)=r−(rTime+aest)(ST(t)+δST(t))    (5)

Рисунок 2. Ошибки в измерении задержки будущего вознаграждения приводят к соответствующей ошибке в субъективной ценности . Если задержка с вознаграждением воспринимается как более ранняя по едва заметной разнице (JND), субъективная ценность воспринимается как большая. Эта ошибка субъективного значения показана на красной полосе и рассчитывается аналитически в разделе «Вклад ошибки измерения времени в ошибку субъективного значения».

Из уравнений (4, 5) теперь мы можем рассчитать JND в субъективном значении как по мере увеличения задержки субъективная ценность уменьшается, т. е. ценность дисконтируется.

Ранее мы показали, что ошибка в субъективном представлении времени примерно линейно связана с субъективным представлением времени в модели накопителя (Namboodiri et al., 2014b), т. е. δ ST(t) = kST (т) + с . Вклад из-за постоянного члена c можно рассматривать как постоянную ошибку считывания, и он довольно мал, за исключением предела ST(t) , приближающегося к нулю. Подставляя это соотношение в уравнение (6), получаем

δSV(r,t)=−(rTime+aest)(kST(t)+c)    (7)

Уравнение (7) можно также переписать с использованием уравнения (4) в виде

δSV(r,t) =−c(rTime+aest)−k(r−SV(r,t))    (8)

Из приведенного выше уравнения видно, что ошибка в субъективной ценности отсроченного вознаграждения линейно связана с падением в субъективной ценности с нулевого времени по прошествии времени. Следовательно, закон Вебера применяется для снижения субъективной ценности отсроченного вознаграждения из-за задержки, т. е. до г − СВ ( р, т ). Другими словами, по мере увеличения задержки и уменьшения субъективной ценности ошибка в изменении субъективной ценности из-за задержки пропорциональна изменению субъективной ценности. В дальнейшем мы будем называть это законом Вебера в ценностном восприятии.

Теперь рассмотрим эффект уменьшения задержки до нуля. Поскольку отрицательный знак в приведенных выше уравнениях указывает только направление изменения, мы опускаем этот знак здесь и далее для расчета шума. Таким образом, когда t = 0, оба уравнения (7, 8) принимают вид

δSV(r,0)=c(rTime+aest)    (9)

величина вознаграждения. Это закон Вебера в восприятии величины, возникающий исключительно из-за ошибки в восприятии бесконечно малой непосредственной задержки, а не исключительно из-за ошибки измерения величины, как это обычно считается. Интересно, что прошлый интервал интегрирования ( T _ime ) увеличивается, что приводит к повышению точности восприятия времени (Namboodiri et al. , 2014b), а также точность восприятия величины вознаграждения. Это новое, непроверенное предсказание представленной здесь версии. Эта временная основа закона Вебера для восприятия величины вознаграждения также предсказывает, что точность представления величины снижается, когда уровень вознаграждения в прошлом высок. Это тоже новое, поддающееся проверке предсказание, которое согласуется с идеей о том, что при высоком уровне вознаграждения снижается потребность в точном представлении вознаграждения (что приводит к увеличению метаболических затрат). Вышеприведенные два прогноза относительно зависимости ошибок в субъективной ценности от предыдущего интервала интегрирования и прошлой ставки вознаграждения изображены на рисунке 3.9.0003

Рис. 3. (A) Доля ошибки Вебера в субъективном значении уменьшается с увеличением предыдущего интервала интегрирования. Это математически представлено в уравнении (8). По сравнению с рисунком 2 (представленным как T _ime на графике справа) прошлый интервал интегрирования на этой панели больше, что уменьшает ошибку субъективного значения при увеличении субъективного значения. Таким образом, дробь Вебера меньше. (B) Доля ошибки Вебера в субъективной ценности увеличивается с увеличением прошлой ставки вознаграждения. Это математически представлено в уравнении (8). По сравнению с рисунком 2 (представленным как низкий уровень a _est на графике справа), прошлый коэффициент вознаграждения на этой панели выше, что увеличивает ошибку в субъективной ценности при уменьшении субъективной ценности. Таким образом, доля Вебера больше.

Приведенная выше трактовка показывает, что шум в восприятии времени приводит к восприятию величины вознаграждения, которое подчиняется закону Вебера. Однако обратите внимание, что для вычисления ошибки субъективной величины (возникающей исключительно из-за шума при измерении бесконечно малой задержки до немедленного вознаграждения) мы до сих пор игнорировали вклад шума в измерение самой величины вознаграждения. Поскольку мы не знаем относительных вкладов этих источников шума, возможно, что источник, связанный со временем, может внести минимальный вклад в общую ошибку восприятия величины вознаграждения. Поэтому в следующем разделе мы представляем модель сенсорного восприятия для величины вознаграждения, а затем вычисляем результирующую ошибку восприятия.

Ошибка сенсорного измерения величины вознаграждения из-за накопления доказательств

В этом разделе мы вычисляем сенсорную ошибку измерения величины вознаграждения (например, ошибка измерения объема водного вознаграждения). Считается, что в некоторых модальностях сенсорный рецептор сам производит скалярный шум (Matthews et al., 1990; Donner et al., 1998; Nieder and Miller, 2003). Хотя это возможно при измерении величины вознаграждения, мы не рассматриваем это простое решение здесь, поскольку нейронные элементы в центральной нервной системе обычно рассматриваются как аппроксимирующие процессы Пуассона, которые имеют шум квадратного корня, а не линейный шум (Rieke et al. , 1999). Скорее, мы рассматриваем ошибки в приписывании ценности данной величине вознаграждения как результат центральных, а не периферийных процессов. Хотя существуют и другие модели закона Вебера в ощущениях (Treisman, 1966; Dehaene, 2003; Deco and Rolls, 2006; Shouval et al., 2013), наша основана на том факте, что измерение любой сенсорной величины должно осуществляться выходит со временем.

С этой целью мы предполагаем, что сенсорный процесс измерения величины осуществляется во времени в небольшом временном окне ощущений. Это сенсорное окно определяется как время, в течение которого существует постоянная скорость сенсорного ввода. Следовательно, мы предполагаем, что величина чистого воспринимаемого вознаграждения пропорциональна времени, которое требуется для интеграции сенсорной информации (например, при питье воды с постоянной скоростью количество получаемой воды пропорционально продолжительности потребления). Альтернативную модель сенсорной интеграции см. в Приложении A1 в дополнительных материалах. Чтобы оценить шум в измерениях, мы предполагаем, что эта сенсорная интеграция может быть описана моделью накопления, аналогичной предыдущим моделям принятия решений, используемым для накопления доказательств (например, Simen et al. , 2011; Brunton et al., 2013). . Далее мы предполагаем, что величина вознаграждения представлена ​​линейно и не подвергается логарифмическому преобразованию, как это было предложено для числового представления (Dehaene, 2003). В оставшейся части этого раздела мы формализуем эту модель накопителя с помощью стохастического дифференциального уравнения, а затем аналитически рассчитаем временную зависимость ее среднего значения и дисперсии.

Если бы нейронная система, осуществляющая эту сенсорную интеграцию, была совершенно бесшумной, мы можем описать модель накопителя следующим дифференциальным уравнением

drt=adt; 0≤t≤tsensory    (10)

Здесь r _t представляет интегрированную величину вознаграждения в данный момент времени. Таким образом, измеренная величина вознаграждения r будет интегральной величиной в конце сенсорного окна, t _{сенсорной} , т. е. r = r _{t сенсорный} . Скорость сенсорного ввода обозначается от до .

Теперь мы ослабим предположение, что сенсорная интеграция бесшумна. Шум в такой накопительной системе может быть вызван двумя источниками: шумом на сенсорном входе и шумом обратной связи в накопителе. Мы предполагаем, что обратная связь представляет собой шум с нулевым средним значением, возникающий в результате сбалансированных возбуждающих/тормозных связей, как и во многих предыдущих работах (например, Simen et al., 2011; Brunton et al., 2013), и что нейроны, выполняющие эти вычисления, могут все можно описать как точечные процессы Пуассона, т. е. дисперсия каждого источника шума будет пропорциональна соответствующему сигналу. Таким образом, дисперсия сенсорного входа будет пропорциональна входу ( a ), а шум обратной связи будет пропорционален r _t . Обозначим константы пропорциональности как b и σ соответственно.

Для простоты сначала предположим, что эти два источника шума независимы и аддитивны. Поскольку дисперсия суммы двух независимых источников суммируется, чистая дисперсия может быть выражена как σ ² r _t + b ² a . Если мы рассматриваем дисперсию шумового члена как постоянную в течение всего интегрирования, ее можно представить, введя дополнительный диффузионный член, который аппроксимирует броуновское движение с бесконечно малой дисперсией σ ² r _t + b ² a в уравнение (10). Таким образом, введение этих источников шума может быть формально описано следующим стохастическим дифференциальным уравнением

drt=adt+σ2rt+b2a  dWt; 0≤t≤tsensory    (11)

W _t представляет собой стандартный винеровский процесс (броуновское движение).

Мы аналитически решим зависимость от времени для первого и второго моментов вышеупомянутого аккумулятора [показанного в уравнении (11)], чтобы вычислить среднее значение и дисперсию в конце сенсорного окна.

Взяв ожидаемые значения с обеих сторон уравнения (11), мы получим

d = adt; 0≤t≤tsensory    (12)

, где < r _t > представляет ожидаемое значение r _t . Поскольку < r ₀ > = 0, мы можем записать решение, полученное путем интегрирования от 0 до t , как

=at    (13)

Уравнение эволюции во времени для < r ² _t > can similarly be calculated by applying Ito’s product rule as

drt2=2rtdrt+(drt)2=2artdt+2rtσ2rt+b2a dWt          +(adt+σ2rt+b2a dWt)20≤t ≤tsensory (14)

с использованием DT ² = 0, DW _T DT = 0 и DW ²

7 = 0 и DW 2

7 = 0 и DW 2 2

7 = 0 и DW 2 2 7 = 0 и DW 2 2 7 = 0 и DW 9036 2 2 2 7 = 0. ожидания обеих сторон, получаем

d=(2+<σ2rt+b2a . σ2rt+b2a>)dt; 0≤t≤tсенсоры    (15)

Упрощая, получаем

d=((σ2+2a)+b2a)dt; 0≤t≤tsensory    (16)

Подставляя из уравнения (13) и интегрируя от 0 до t с граничным условием < r ² _{t = 0 0} > 9 0 = 90 856 получаем

=a(σ2+2a)t22+b2at;0≤t≤tsensory    (17)

Таким образом, дисперсию r _t можно вычислить как

var(rt)=< rt2>−2=aσ2t22+b2at; 0​≤t​≤tсенсоры    (18)

Таким образом, коэффициент вариации r _t равен

CV(rt)=σ22a+b2at; 0

Поскольку измеренная величина вознаграждения представляет собой интегрированную величину после сенсорного окна, CV измерения можно записать как

CV(r)=σ22a+b2atsensory    (20)

или

CV(r)=σ22a+b2r    (21)

Если предположить, что скорость сенсорного ввода постоянна, приведенное выше уравнение показывает, что, за исключением низких величин вознаграждения, CV постоянна, т. е. закон Вебера выполняется примерно для восприятия величины вознаграждения. Если о ² / a велико по сравнению с b ² , постоянный член будет преобладать, и CV будет почти точно постоянным. Эти аналитические результаты подтверждаются численным моделированием, как показано на рисунке 4.

Рисунок 4. Подтверждающее моделирование (см. Методы) аналитического решения модели накопителя, в которой сенсорный шум и шум обратной связи аддитивно комбинируются . Красная линия показывает результат аналитического расчета, выраженного в уравнении (21), где сенсорный сигнал ( a ), величина сенсорного шума ( b ) и величина шума обратной связи (σ) варьируются. Черными точками показаны результаты численного моделирования. Результаты хорошо аппроксимируют закон Вебера, но для низких величин вознаграждения и высокого сенсорного шума ( b ).

Математика аккумулятора, показанная в уравнении (11), очень похожа на уравнение (9) в (Simen et al. , 2011). Но есть и существенные различия в значении терминов. Во-первых, наша модель предназначена для восприятия величины вознаграждения, тогда как их модель предназначена для производства временных интервалов. Во-вторых, как следствие, в то время как в нашей модели предполагается, что скорость сенсорного ввода является постоянной, они предполагают, что скорость накопления настроена на интервал, который нужно отсчитывать. По этой причине их модель может давать скалярную синхронизацию только для производства временных интервалов, а не для измерения/восприятия временных интервалов, где коэффициент вариации уменьшается обратно пропорционально квадратному корню из интервала [аналогично второму члену в уравнении (21) ].

Уравнения (11–21) предполагают, что сенсорный входной шум является аддитивным по отношению к шуму обратной связи. Вместо этого, если бы этот шум действительно был мультипликативным, уравнение (11) изменилось бы на

drt=adt+σb2art dWt; 0≤t≤tsensory    (22)

В этом случае CV можно рассчитать аналогично (показано в Приложении A2 в дополнительных материалах)

CV(r)=σb2    (23)

Таким образом, когда сенсорная и обратная связь шумы умножаются, коэффициент вариации не зависит от величины сенсорного сигнала ( и ).

Опять же, мы выполнили подтверждающее численное моделирование уравнения (22), результаты которого показаны на рисунке 5. Следовательно, если сенсорный входной шум является мультипликативным, коэффициент вариации точно постоянен, что делает закон Вебера точным. Вместо этого, если сенсорный входной шум является аддитивным, коэффициент вариации показывает отклонения от точного закона Вебера при низких величинах вознаграждения.

Рис. 5. Подтверждающее моделирование (см. Методы) аналитического решения модели накопителя, в которой сенсорный шум и шум обратной связи комбинируются мультипликативно . Красная линия показывает результат аналитического расчета, выраженного в уравнении (23), в котором изменяются сенсорный сигнал ( a ), величина сенсорного шума ( b ) и величина шума обратной связи (σ). Черными точками показаны результаты численного моделирования. Здесь закон Вебера точен.

Рассмотренная выше накопительная модель аналогична той, которую мы ранее предложили для представления субъективного времени (Namboodiri et al. , 2014b), с двумя отличиями. Самое важное отличие заключается в том, что, хотя субъективное время считается нелинейным преобразованием реального времени, предполагается, что субъективное вознаграждение линейно пропорционально реальному вознаграждению. Из-за этой разницы накопитель величины вознаграждения поддается анализу, в отличие от накопителя субъективного времени, для которого аналитическое решение было приблизительным (Namboodiri et al., 2014b). Другое отличие заключается в том, что, поскольку накопитель величины вознаграждения работает на сенсорном входе (в отличие от накопителя субъективного времени), вклад этого сенсорного шума также был включен.

Комбинированная ошибка измерения субъективной ценности из-за времени и величины

Теперь у нас есть все элементы для расчета ошибки субъективной ценности отсроченного вознаграждения, возникающей из-за ошибок измерения величины и времени (рис. 6).

Рисунок 6. На ошибку субъективного значения влияют ошибки измерения как задержки (как показано на рисунке 2), так и величины вознаграждения . Эта комбинированная ошибка рассчитывается аналитически в разделе «Комбинированная ошибка из-за измерения времени и величины субъективного значения».

Возвращаясь к уравнению (4), если мы рассмотрим эффект добавления JND как r , так и ST(t) , мы увидим, что добавление JND r приводит к увеличению SV ( r, t ), добавление JND ST(t) приводит к уменьшению (из-за временного дисконтирования). Поскольку нас интересует только чистая ошибка, то для согласования направления изменения мы рассмотрим влияние ошибки как на r , так и на ST(t) , добавив JND r и вычтя JND ST(t) . Таким образом, мы получаем следующее уравнение Таким образом, используя уравнение (4), ошибка субъективного значения δ SV ( r, t ) может быть записана как

δSV(r,t)=δr(1−ST(t)Time)+(rTime +aest)δST(t)                  + δrδST(t)Time    (25)

Из уравнения (4), (1−ST(t)Time)=SV(r,t)+aestST(t)r. Следовательно, уравнение (25) принимает вид

δSV(r,t)=δrr(SV(r,t)+aestST(t))+(rTime+aest)δST(t)                   + δrδST(t)Time    (26)

Для простоты рассмотрим точная форма закона Вебера для сенсорного измерения r . Поэтому пишем δrr=l, где l — дробь Вебера.

Из уравнений (6), (8) второй член в RHS равен c(rTime+aest)+k(r−SV(r,t)), где δ ST ( t ) = кСТ ( т ) + с .

Перед вычислением ошибки субъективной ценности при любой задержке мы сначала вычислим ее значение для немедленного вознаграждения, где t = 0 и ST ( t ) = 0. Из уравнения (26) это может быть записывается как

δSV(r,0)=lr+c(rTime+aest)+lcrTime    (27)

Упрощая, получаем

δSV(r,0)=r(l(1+cTime)+cTime) +caest    (28)

Приведенное выше уравнение подчиняется закону Вебера для восприятия величины вознаграждения, являющемуся результатом ошибок как в измерении величины, так и в измерении бесконечно малой задержки до немедленного вознаграждения. Как видно, дробь Вебера [наклон δ SV(r, 0) по отношению к r ] зависит от T _ime , прошедшего интервала интегрирования. Таким образом, мы прогнозируем, что даже внутри индивидуума доля Вебера в восприятии величины вознаграждения (субъективная ценность немедленного вознаграждения) может меняться в зависимости от контекста по мере изменения прошедшего интервала интегрирования. Направление этого изменения будет таким, что чем лучше восприятие времени, тем лучше восприятие величины вознаграждения. Кроме того, как упоминалось ранее после уравнения (9), приведенное выше уравнение также предсказывает, что чем больше опытная норма вознаграждения, тем больше ошибка в восприятии величины вознаграждения. Таковы сильные фальсифицируемые предсказания нашего описания.

Теперь мы вычисляем ошибку субъективной ценности при заданной задержке t из-за ошибок измерения как времени, так и величины вознаграждения. Из уравнения (26) получаем +lr(kST(t)+c)Время    (29)

Упрощая, получаем

δSV(r,t)=(l−k)SV(r,t)+(laest+lrkTime)ST(t)                        + c+ +l)cest(1+l)rest (30)

Поскольку нас интересует шум в субъективной ценности постоянной величины вознаграждения, задержанной на различные величины, если мы рассматриваем r как константу (на данный момент), мы можем написать [используя уравнение (4)] ST (t)=r−SV(r,t)rTime + aest. Группируя члены, которые пропорциональны SV ( r, t ) отдельно от других членов, приведенное выше уравнение становится

δSV(r,t)=(l−k−laestTime+rkaestTime+r)SV(r,t)                        +(r((1+l)cTime+k+laestTime+rkaestTime+r)+caest3) )

Приведенное выше уравнение также подчиняется закону Вебера. Таким образом, мы показали, что ошибка в субъективной ценности данного вознаграждения, отсроченного на разные суммы, пропорциональна субъективной ценности при каждой данной задержке. Опять же, доля Вебера зависит от среды вознаграждения животного, поскольку она зависит от r , a _est и T _име .

Аналогичным образом мы можем рассчитать субъективную ошибку значения при заданной задержке для различных величин вознаграждения. Для этого мы заменяем r на [используя уравнение (4)] r=SV(r,t)+aestST(t)1−ST(t)Time в переписанной версии уравнения (25), как показано ниже.

δSV(r,t)=lr(1−ST(t)Time)+c(rTime+aest)                         + k(rTime+aest)ST(t)+lr(kST)2 3 3 3 )

Таким образом,

δSV(r,t)=l(SV(r,t)+aestST(t))+r(1+l)c+kST(t)Time                                       ))    (33)

Или,

t)(1+l)c+kST(t)Time−ST(t)+c+kST(t))    (34)

, где ST(t)=t1+tTime.

Это тоже соответствует закону Вебера. Таким образом, мы также показали, что ошибка в субъективной ценности при заданной задержке для различных величин вознаграждения пропорциональна субъективной ценности.

Обсуждение

Ранее мы представили общую теорию межвременного принятия решений и восприятия времени (TIMERR), которая объясняет многие хорошо зарекомендовавшие себя наблюдения в этих областях (Namboodiri et al., 2014b). Наша теория утверждает, что решения животных являются следствием максимизации уровня вознаграждения в ограниченном временном окне, включая прошлый интервал интеграции и задержку текущего вознаграждения. Интересно, что мы показали, что репрезентация времени также связана с прошлым интервалом интеграции в нашей структуре, и что у импульсивных (низкая терпимость к задержкам вознаграждения) людей нарушено восприятие времени. Затем мы продемонстрировали, что ошибка в восприятии времени приблизительно скалярна, а отклонение от точного закона Вебера зависит от прошедшего интервала интегрирования.

В этой статье мы расширяем результаты нашей предыдущей работы, чтобы рассмотреть роль ошибки в восприятии времени на восприятие величин вознаграждения и субъективных значений отложенных вознаграждений. Мы показали, что ошибка в восприятии бесконечно малой задержки немедленного вознаграждения влияет на восприятие величины вознаграждения в соответствии с законом Вебера. Поскольку сенсорное измерение вознаграждения должно проводиться во времени, мы вывели закон Вебера для ощущения величины вознаграждения, приняв модель накопителя (для этой сенсорной интеграции) с обратной связью Пуассона со сбалансированным возбуждением/торможением. Это может быть основной причиной соблюдения закона Вебера при восприятии величины вознаграждения животными. Впоследствии мы показали, что в TIMERR сочетание ошибок измерения времени и величины вознаграждения при субъективном изменении значения отсроченного вознаграждения также соответствует закону Вебера. Важно отметить, что доли Вебера, по прогнозам, зависят от истории вознаграждения животного, что обеспечивает сильное, опровержимое предсказание нашей теории, наряду с предсказанной корреляцией между ошибками в восприятии времени и оценкой величины вознаграждения.

На первый взгляд, можно предположить, что поскольку восприятие величины вознаграждения подчиняется закону Вебера, то же самое должно происходить и с субъективной ценностью отсроченного вознаграждения. На самом деле такое утверждение уже делалось ранее (Cui, 2011) без признания того, что для этого требуется конкретное отношение между субъективной ценностью, величиной вознаграждения, задержкой вознаграждения и восприятием задержки. Из нашего аналитического вывода, представленного выше, очевидно, что закон Вебера в изменении субъективной ценности является следствием особых форм функции дисконтирования (субъективная ценность отсроченного вознаграждения, деленная на субъективную ценность этого вознаграждения при немедленном предъявлении) и субъективной репрезентации времени. которые вытекают из нашей теории. На самом деле, если сделать стандартные предположения о (1) законе Вебера в измерении величины вознаграждения, (2) гиперболической функции дисконтирования (Эйнсли, 1974; Фредерик и др., 2002; Каленшер и Пеннарц, 2008 г.; Cui, 2011) и (3) линейное субъективное представление времени, которое подчиняется закону Вебера (Gibbon, 1977; Gibbon et al., 1984), результирующая ошибка в субъективной ценности отсроченного вознаграждения далеко не пропорциональна субъективной ценности , как показано в Приложении A3 в дополнительных материалах.

Недавние эксперименты показали, что представление величины или ценности вознаграждения зависит не только от рассматриваемого вознаграждения, но и от других доступных вариантов (Huber et al. , 19).82; Бейтсон и др., 2003 г.; Луи и др., 2013). Недавняя нейроэкономическая модель (Louie et al., 2013), использующая разделяющую схему нормализации, в которой каждое отдельное вознаграждение сравнивается с другими доступными вариантами, может привести к такой зависимости от контекста. В свете этих результатов можно поставить под сомнение наше предположение об абсолютном коде величины вознаграждения, то есть наше предположение о том, что величина вознаграждения представлена ​​только на основе величины интересующего вознаграждения. Таким образом, важно отметить, что наша теория предсказывает контекстно-зависимый выбор даже в предположении, что представление величины вознаграждения не зависит от других доступных вариантов. Это связано с тем, что на субъективную ценность вознаграждения (поскольку каждое вознаграждение фактически представляет собой отсроченное вознаграждение) влияет оценка животным его прошлой степени вознаграждения [уравнение (1)]. Таким образом, наличие отвлекающих факторов влияет на субъективную ценность награды из-за влияния на прошлую норму вознаграждения в экспериментах с последовательным выбором. Кроме того, текущие варианты могут повлиять на оценку вознаграждения за опыт (Namboodiri et al., 2014a). Далее, как показано в уравнениях (9, 28), чем больше значение прошлой ставки вознаграждения, тем больше ошибка (доля Вебера) в представлении вознаграждения. Таким образом, наша теория предсказывает, что чем больше значение отвлекающего фактора (тем самым увеличивая прошлую норму вознаграждения), тем выше ошибки при выборе между двумя вознаграждениями, в соответствии с экспериментальными наблюдениями, показанными в Louie et al. (2013). Ключевое различие между нашей учетной записью и учетной записью нормализации с разногласиями (Louie et al., 2013) заключается в том, что в нашей учетной записи зависимость от контекста связана с оценкой уровня вознаграждения в прошлом, тогда как при нормализации с разногласиями контекстная зависимость основана только на доступные на данный момент опции.

Ранее существовали модели того, как закон Вебера в отношении величины вознаграждения и восприятия времени влияет на решения животных в контексте внешней изменчивости по этим двум измерениям (см. Kacelnik and Bateson, 1996; Kacelnik and Brito e Abreu, 1998). Эти модели успешно объясняют, почему животные предпочитают изменчивость во времени, а не в величине вознаграждения, по сравнению с фиксированными вариантами того же среднего (см. Kacelnik and Bateson, 1996; Kacelnik and Brito e Abreu, 19).98). Однако они не предлагают происхождение закона Вебера для величины вознаграждения или времени, а также не рассчитывают чистую ошибку из-за обоих источников шума. Уникально для нашей теории, мы предсказываем систематическую связь между историей вознаграждения животных и их восприятием этих величин.

Методы

Подтверждающее моделирование, выполненное для рисунков 4, 5, интегрированных уравнений (11, 22) соответственно с использованием метода Эйлера-Маруямы. Таким образом, версия уравнения с дискретным временем, используемая для рисунка 4, была

rt+Δt=rt+aΔt+σ2rt+b2aΔtN(0,1)

и для рисунка 5 было

rt+Δt=rt+aΔt+σbartΔtN(0,1)

где 1) — стандартное нормальное распределение. Размер шага интегрирования Δt был установлен равным 0,001 единицы. Параметры были изменены, как показано в легенде рисунка. В каждом случае для инициализации моделирования использовалось одно и то же случайное начальное число.

Заявление о конфликте интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Благодарности

Эта работа была профинансирована NIMH (R01 MH084911 и R01 MH093665) для Marshall G. Hussain Shuler.

Дополнительный материал

Дополнительный материал к этой статье можно найти в Интернете по адресу: http://www.frontiersin.org/journal/10.3389/fnint.2014.00079/abstract

Ссылки

Ainslie, G.W. (1974). Импульсный контроль у голубей. Дж. Экспл. Анальный. Поведение . 21, 485–489. doi: 10.1901/jeab.1974.21-485

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Акре, К. Л., и Джонсен, С. (2014). Психофизика и эволюция поведения. Тренды Экол. Эвол . 29, 291–300. doi: 10.1016/j.tree.2014.03.007

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Балчи Ф., Фристоун Д., Саймен П., Десуза Л., Коэн Дж. Д. и Холмс П. (2011). Оптимальная временная оценка риска. Перед. интегр. Нейроски . 5:56. doi: 10.3389/fnint.2011.00056

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Бейтсон, М., Хили, С. Д., и Херли, Т. А. (2003). Контекстно-зависимые решения о кормлении у рыжих колибри. Проц. биол. Наука . 270, 1271–1276. doi: 10.1098/rspb.2003.2365

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Бейтсон М., Касельник А., Роуд С. П. и Окс О. (1995). Точность запоминания количества кормового скворца Sturnus vulgaris . Аним. Поведение . 50, 431–443. дои: 10.1006/anbe.1995.0257

CrossRef Полный текст | Google Scholar

Би, Массачусетс, Велес, А., и Форестер, Дж. Д. (2012). Различение уровня звука серыми древесными лягушками при наличии и отсутствии хорового шума. J. Акустический. соц. Я . 131, 4188–4195. doi: 10.1121/1.3699271

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Беран, MJ (2007). Обезьяны-резусы ( Macaca mulatta ) перечисляют большие и маленькие последовательно предъявляемые наборы предметов, используя аналоговые числовые представления. Дж. Эксп. Психол. Аним. Поведение Процесс . 33, 42–54. doi: 10.1037/0097-7403.33.1.42

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Бланшар, Т. С., Пирсон, Дж. М., и Хейден, Б. Я. (2013). Задержки после вознаграждения и систематические погрешности в измерениях временного дисконтирования животных. Проц. Натл. акад. науч. США . 110, 15491–15496. doi: 10.1073/pnas.1310446110

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Брантон, Б.В., Ботвиник, М.М., и Броди, К.Д. (2013). Крысы и люди могут оптимально накапливать данные для принятия решений. Наука 340, 95–98. doi: 10.1126/science.1233912

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Буэти, Д., и Уолш, В. (2009). Теменная кора и представление времени, пространства, числа и других величин. Филос. Транс. Р. Соц. Лонд. Б биол. Наука . 364, 1831–1840 гг. дои: 10.1098/rstb.2009.0028

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Buhusi, CV, and Meck, WH (2005). Что заставляет нас тикать? Функциональные и нейронные механизмы интервальной синхронизации. Нац. Преподобный Нейроски . 6, 755–765. doi: 10. 1038/nrn1764

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Кантлон, Дж. Ф., и Браннон, Э. М. (2006). Общая система заказа малых и больших чисел у обезьян и людей. Психология. Наука . 17, 401–406. doi: 10.1111/j.1467-9280.2006.01719.x

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Кордес С., Гельман Р., Галлистел С. Р. и Уэлен Дж. (2001). Сигнатуры изменчивости отличают вербальный счет от невербального как для больших, так и для малых чисел. Психон. Бык. Версия . 8, 698–707. doi: 10.3758/BF03196206

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Цуй, Х. (2011). Гиперболическое дисконтирование возникает из скалярного свойства временных интервалов. Перед. интегр. Нейроски . 5:24. doi: 10.3389/fnint.2011.00024

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Деко, Г. , и Роллс, Э. Т. (2006). Принятие решений и закон Вебера: нейрофизиологическая модель. евро. Дж. Нейроски . 24, 901–916. doi: 10.1111/j.1460-9568.2006.04940.x

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Дехане, С. (2003). Нейронная основа закона Вебера-Фехнера: логарифмическая мысленная числовая линия. Познание тенденций. Наука . 7, 145–147. doi: 10.1016/S1364-6613(03)00055-X

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Дехане С. и Брэннон Э. (ред.). (2011). Пространство, время и число в мозгу, 1-е изд. . Сан-Диего, Калифорния: Academic Press; Elsevier Inc.

Доннер К., Хемила С. и Коскелайнен А. (1998). Световая адаптация фотоответов колбочек изучалась на уровне фоторецепторов и ганглиозных клеток в сетчатке лягушки. Виз. Рез . 38, 19–36. doi: 10.1016/S0042-6989(97)00144-2

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Друа-Воле, С. (2013). Восприятие эмоций и величин: число и длина пополам. Перед. Нейроробот . 7:24. doi: 10.3389/fnbot.2013.00024

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Форрест, Т. Г. (1994). От отправителя к получателю: распространение и влияние окружающей среды на акустические сигналы. утра. Зоол . 34, 644–654. doi: 10.1093/icb/34.6.644

Полный текст CrossRef | Google Scholar

Фредерик С., Левенштейн Г., Донохью Т.О. и Донохью Т.Э.Д.О. (2002). Дисконтирование времени и временные предпочтения: критический обзор. Ж. эконом. Лит . 40, 351–401. doi: 10.1257/jel.40.2.351

CrossRef Полный текст | Академия Google

Gallistel, CR (2011). «Ментальные величины», в Space, Time and Number in the Brain , eds S. Dehaene and E. Brannon (Сан-Диего, Калифорния: Academic Press; Elsevier Inc.), 3–12. doi: 10.1016/B978-0-12-385948-8.00001-3

CrossRef Полный текст | Google Scholar

Гиббон, Дж. (1977). Теория скалярного ожидания и закон Вебера в хронометраже животных. Психология. Версия . 84, 279–325. doi: 10.1037/0033-295X.84.3.279

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Гиббон, Дж., Черч, Р.М., и Мек, У.Х. (1984). «Скалярная синхронизация в памяти», в Timing and Time Perception , eds J. Gibbon and L. Allan (Нью-Йорк, штат Нью-Йорк: Нью-Йоркская академия наук), 52–77.

Опубликован Аннотация | Опубликован полный текст | Google Scholar

Хубер Дж., Пейн Дж. В. и Путо К. (1982). Добавление асимметрично доминируемых альтернатив: нарушение регулярности и гипотеза подобия. Дж. Консум. Рез . 9, 90–98. дои: 10.1086/208899

Полнотекстовая перекрестная ссылка | Google Scholar

Касельник А. и Бейтсон М. (1996). Рискованные теории — влияние дисперсии на решения о кормлении. Интегр. Комп. Биол . 36, 402–434. doi: 10.1093/icb/36.4.402

Полный текст CrossRef | Google Scholar

Касельник А. и Брито и Абреу Ф. (1998). Рискованный выбор и закон Вебера. Ж. Теор. Биол . 194, 289–298. doi: 10.1006/jtbi.1998.0763

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Академия Google

Каленшер, Т., и Пеннарц, К.М.А. (2008). Стоит ли синица в руке двух в будущем? Нейроэкономика межвременного принятия решений. Прог. Нейробиол . 84, 284–315. doi: 10.1016/j.pneurobio.2007.11.004

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Киллин П.Р., Кейт Х. и Тран Т. (1993). Выбор корма для голубей: чем больше, тем лучше. Дж. Экспл. Анальный. Поведение . 60, 203–217. дои: 10.1901/jeab.1993.60-203

Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Луи К., Хау М. В. и Глимчер П. В. (2013). Нормализация — это общий нейронный механизм для контекстно-зависимого принятия решений. Проц. Натл. акад. науч. США . 110, 6139–6144. doi: 10.1073/pnas.1217854110

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Мателл, М.С., и Мек, У.Х. (2000). Нейропсихологические механизмы интервального временного поведения. Bioessays 22, 94–103. doi: 10.1002/(SICI)1521-1878(200001)22:1%3C94::AID-BIES14%3E3.0.CO;2-E

Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Мэтьюз Х. Р., Фейн Г. Л., Мерфи Р. Л. и Лэмб Т. Д. (1990). Световая адаптация фоторецепторов колбочек саламандры: роль цитоплазматического кальция. Дж. Физиол . 420, 447–469.

Опубликован Аннотация | Опубликован полный текст | Google Scholar

Намбудири В.М.К., Михалас С. и Хуссейн Шулер М.Г. (2014a). Рационализация принятия решений: понимание стоимости и восприятия времени. Время восприятия времени. Версия . 1.

Намбудири, В.М.К., Михалас, С., Мартон, Т.М., и Хуссейн Шулер, М. Г. (2014b). Общая теория межвременного принятия решений и восприятия времени. Перед. Поведение Нейроски . 8:61. doi: 10.3389/fnbeh.2014.00061

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Нидер А. и Миллер Э. К. (2003). Кодирование когнитивной величины: сжатое масштабирование числовой информации в префронтальной коре приматов. Нейрон 37, 149–157. doi: 10.1016/S0896-6273(02)01144-3

Опубликовано Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Рике Ф., Варланд Д., ван Стивенинк Р. и Биалек В. (1999). Шипы: изучение нейронного кода . Кембридж, Массачусетс: MIT Press.

Ровамо, Дж., Мустонен, Дж., и Нясанен, Р. (1995). Передаточная функция нейронной модуляции зрительной системы человека при различных эксцентриситетах. Виз. Рез . 35, 767–774. дои: 10.1016/0042-6989(94)00171-H

Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Шоувал Х. , Агарвал А. и Гаворник Дж. (2013). Масштабирование ошибок восприятия может предсказать форму кривых настройки нейронов. Физ. Преподобный Письмо . 110:168102. doi: 10.1103/PhysRevLett.110.168102

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Симен П., Балчи Ф., де Соуза Л., Коэн Дж. Д. и Холмс П. (2011). Модель интервального времени с помощью нейронной интеграции. Дж. Нейроски . 31, 9238–9253. doi: 10.1523/JNEUROSCI.3121-10.2011

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Стивенс Д. В. и Кребс Дж. Р. (1986). Теория собирательства . Принстон, Нью-Джерси: Издательство Принстонского университета.

Google Scholar

Трейсман, М. (1966). Статистическая модель принятия решений для сенсорной дискриминации, которая предсказывает закон Вебера и другие сенсорные законы: некоторые результаты работы компьютера. Восприятие. Психофиз . 1, 203–230. doi: 10.3758/BF03215786

Полный текст CrossRef | Google Scholar

Уолш, В. (2003). Теория величины: общие корковые метрики времени, пространства и количества. Познание тенденций. Наука . 7, 483–488. doi: 10.1016/j.tics.2003.09.002

Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar

Вебер, Э. Х. (1978). Осязание, 1-е издание . Лондон: Академическая пресса.

Уэлен, Дж., Галлистел, К.Р., и Гельман, Р. (1999). Невербальный счет у людей: психофизика представления чисел. Психология. Наука . 10, 130–137. doi: 10.1111/1467-9280.00120

Полный текст CrossRef | Google Scholar

Макс Вебер | Биография, образование, теория, социология, книги и факты

Макс Вебер

Смотреть все медиа

Дата рождения:

21 апреля 1864 г. Эрфурт Пруссия

Умер:

14 июня 1920 г. (56 лет) Мюнхен Германия

Известные работы:

«Протестантская этика и дух капитализма»

Объекты исследования:

кальвинизм протестантская этика капитализм

Просмотреть весь связанный контент →

Популярные вопросы

Когда родился Макс Вебер?

Макс Вебер родился 21 апреля 1864 года.

Когда умер Макс Вебер?

Что написал Макс Вебер?

Макс Вебер написал Протестантская этика и дух капитализма (1904–05), Экономика и общество (1922), Всеобщая экономическая история (1923) и другие работы.

Чем известен Макс Вебер?

Макс Вебер известен своим тезисом о том, что «протестантская этика» (предположительно протестантские ценности трудолюбия, бережливости, эффективности и аккуратности) способствовала экономическому успеху протестантских групп на ранних стадиях европейского капитализма.

Сводка

Прочтите краткий обзор этой темы

Макс Вебер (родился 21 апреля 1864, Эрфурт, Пруссия [Германия] — умер 14 июня 1920, Мюнхен, Германия), немецкий социолог и политический экономист, наиболее известный своей диссертацией о «протестантской этике», касающейся протестантизма к капитализму и за его идеи о бюрократии.

Молодость и семейные отношения

Вебер был старшим сыном Макса и Элен Вебер. Его отец был честолюбивым либеральным политиком, который вскоре присоединился к более послушным, пробисмарковским «национал-либералам» и перевез семью из Эрфурта в Берлин, где стал членом прусской палаты депутатов (1868–1899 гг.).7) и Рейхстаг (1872–84). Вебер-старший зарекомендовал себя как неотъемлемая часть берлинской социальной среды и принимал видных политиков и ученых в доме Вебера.

Мать социолога выросла в кальвинистской ортодоксальности. Хотя она постепенно приняла более терпимое богословие, ее пуританская мораль никогда не уменьшалась. В результате общественная деятельность ее мужа отдалила ее от него, особенно когда он отверг ее продолжительное горе после смерти двух их детей. Он, в свою очередь, принял дома традиционно авторитарные манеры и требовал от жены и детей абсолютного послушания. Считается, что эта унылая домашняя обстановка, отмеченная конфликтами между родителями Вебера, способствовала внутренней агонии, преследовавшей Вебера во взрослой жизни.

Вебер ушел из дома, чтобы поступить в Гейдельбергский университет в 1882 году, прервав учебу через два года, чтобы отработать год военной службы в Страсбурге. За это время он очень сблизился с семьей сестры своей матери Иды Баумгартен и с ее мужем, историком Германом Баумгартеном, оказавшим глубокое влияние на интеллектуальное развитие Вебера.

Однако после увольнения из армии отец попросил Вебера закончить учебу в Берлинском университете, чтобы он мог жить дома, изучая юридическую и экономическую историю. Возможно, это произошло потому, что его отец считал влияние Баумгартенов подрывным. С 1884 г. до женитьбы в 189 г.3 Вебер покинул семейный дом только на один семестр учебы в Геттингене в 1885 году и на несколько коротких периодов в составе своего военного резерва.

Ранняя карьера

Таким образом, большую часть академических лет своего становления Вебер провел в доме своего детства, где он постоянно подвергался конфликту интересов своих родителей. Поскольку в середине и конце 20-летнего возраста он работал одновременно на двух неоплачиваемых стажировках — помощником юриста и университетским ассистентом, — он не мог позволить себе жить самостоятельно до осени 189 года.3. В то время он получил временную должность преподавателя юриспруденции в Берлинском университете и женился на Марианне Шнитгер, троюродной сестре, которая стала его биографом и редактором его собрания сочинений. Марианна Вебер также была выдающимся социологом и одной из первых фигур в области феминистской социологии.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

После женитьбы Вебер следовал принудительному режиму работы, который он начал после своего возвращения в Берлин в 1884 году. Вебер полагал, что только благодаря такому дисциплинированному труду он мог предотвратить естественную склонность к баловству и лени, которые могли привести к эмоциональному и духовному кризису.

Огромная способность Вебера к дисциплинированному интеллектуальному усилию в сочетании с его бесспорным талантом привели к его стремительному профессиональному росту. Через год после своего назначения в Берлине он стал профессором политической экономии во Фрайбурге, а в следующем году (1896 г.) он получил эту должность в Гейдельберге. Защитив докторскую и постдокторскую диссертации по аграрной истории Древнего Рима и эволюции средневековых торговых обществ соответственно, Вебер написал всесторонний анализ аграрных проблем Восточной Германии для одного из важнейших академических обществ страны — Союза социальной политики. (1890). Он также написал важные эссе о немецкой фондовой бирже и социальном упадке латинской античности. В эти годы он был политически активен, работая с леволиберальным Протестантским социальным союзом.

Фрайбургский адрес

Кульминацией его ранней научной карьеры стала его инаугурационная речь во Фрайбурге в 1895 году, в которой он объединил около пяти лет изучения аграрных проблем Германии к востоку от Эльбы в сокрушительный обвинительный акт против правящей юнкерской аристократии как исторически устаревшей. Однако, по мнению Вебера, существующие либеральные партии были не в состоянии бросить вызов юнкерам и заменить их. Рабочий класс также не был готов взять на себя ответственность за власть. Только нация в целом, доведенная до политической зрелости сознательной политикой заморской имперской экспансии, могла довести Германию до уровня политической зрелости, достигнутого французами в революционную и наполеоновскую эпохи и британцами в ходе их имперской экспансии. в 19век. Фрайбургское выступление Вебера, таким образом, продвигало идеологию «либерального империализма», привлекая к своей поддержке таких видных либеральных публицистов, как Фридрих Науманн и Ганс Дельбрюк.

В течение нескольких месяцев после смерти отца в августе 1897 года молодого ученого одолевала растущая нервозность. Его возвращение к преподаванию осенью принесло короткую передышку, которая закончилась в начале 1898 г. первыми признаками нервного срыва, который вывел его из строя между серединой 1898 и 1903 гг. В течение пяти лет он периодически помещался в лечебницу, страдая от внезапных рецидивов после медленного выздоровления. и тщетные попытки разорвать такие циклы путешествиями. Он оставил свою профессуру в Гейдельберге в разгар болезни.

Мюнхен | Германия, история, население, Октоберфест и факты

Популярные вопросы

Где находится Мюнхен?

Мюнхен расположен на юге Германии и является столицей земли Бавария. Он расположен примерно в 30 милях (50 км) к северу от края Альп и вдоль реки Изар, которая протекает через центр города.

Как называется Мюнхен в Германии?

Мюнхен в Германии называется München, что означает «Дом монахов» и относится к его происхождению в бенедиктинском монастыре в Тегернзее, который, вероятно, был основан в 750 году нашей эры.

Какие основные музеи и художественные галереи Мюнхена?

Мюнхен уже давно является центром искусства и имеет выдающиеся музеи и художественные галереи. Примерами могут служить Глиптотека, Старая пинакотека и Новая (Новая) пинакотека. Бывший городской арсенал на Якобсплац теперь является муниципальным музеем. В дополнение к ним находятся Музей-резиденция и Немецкий музей.

Какой знаменитый праздник отмечается в Мюнхене?

Мюнхен известен своим пивом и ежегодным празднованием Октоберфеста.

Сводка

Прочтите краткий обзор этой темы

Мюнхен , Германия Мюнхен , город, столица Баварии Земля (земля), южная Германия. Это крупнейший город Баварии и третий по величине город Германии (после Берлина и Гамбурга). Мюнхен, безусловно, самый большой город на юге Германии, находится примерно в 30 милях (50 км) к северу от края Альп и вдоль реки Изар, которая протекает через центр города. Поп. (2011) 1 348 335; (оценка 2021 г.) 1 487 708.

История

Мюнхен, или Мюнхен («Дом монахов»), ведет свое происхождение от бенедиктинского монастыря в Тегернзее, который, вероятно, был основан в 750 г. н.э. В 1157 году Генрих Лев, герцог Баварии, предоставил монахам право основать рынок там, где дорога из Зальцбурга пересекалась с рекой Изар. В следующем году был построен мост через Изар и укреплена рыночная площадь.

В 1255 году Мюнхен стал домом для рода Виттельсбахов, унаследовавших герцогство Баварское в 1180 году. Более 700 лет Виттельсбахи были тесно связаны с судьбой города. В начале 14 века первый из династии Виттельсбахов императоров Священной Римской империи Людовик IV (Людовик Баварский) расширил город до размеров, в которых он оставался до конца 18 века. При баварском курфюрсте Максимилиане I (159 г.7–1651), могущественного и эффективного правителя, Мюнхен рос в богатстве и размерах и процветал до Тридцатилетней войны. Он был оккупирован шведами при Густаве II Адольфе (Gustavus Adolphus) в 1632 году, а в 1634 году эпидемия чумы унесла жизни около трети его населения.

Третьим Виттельсбахом, оставившим свой след в сообществе, был Людовик I, король Баварии с 1825 по 1848 год. Людовик спланировал и создал современный Мюнхен, а его архитекторы воплотили характерный облик города в спроектированных ими общественных зданиях. 19Век был величайшим периодом роста и развития Мюнхена. Протестанты впервые стали гражданами города, который до этого был чисто римско-католическим. Население города со 100 000 человек в 1854 году выросло до 500 000 к 1900 году. Культурное значение Мюнхена в Европе возросло, когда Людовик II, защищая композитора Рихарда Вагнера, возродил его славу города музыки и сцены.

Правление династии Виттельсбахов окончательно закончилось добровольным изгнанием Людовика III 19 ноября18, а после Первой мировой войны Мюнхен стал рассадником правого политического брожения. Именно в Мюнхене Адольф Гитлер вступил в нацистскую партию и стал ее лидером. Пивной погреб, где он проводил собрания, приведшие к Пивному путчу («восстанию») против баварских властей в ноябре 1923 года, все еще можно увидеть. Во время Второй мировой войны Мюнхен сильно пострадал от бомбардировок союзников, в результате которых было разрушено более 40 процентов его зданий.

Современный город

Посетите Мюнхен, чтобы познакомиться с красивыми площадями города, продовольственным рынком, Английским садом и величественной пивоварней Хофбройхаус

Посмотреть все видео к этой статье

В прошлом Мюнхен экономически страдал из-за удаленности от морских портов и угольных шахт Рурской области. Но эта ситуация улучшилась, когда стали широко использоваться другие виды топлива, помимо угля. Мюнхен перешел от тяжелой промышленности к легкой, к производству, например, точных приборов, оптических и электрических приборов, аэрокосмической и другой высокотехнологичной продукции, а также к производству продуктов питания, косметики и одежды. В городе есть несколько крупнейших пивоварен в Германии, он славится своим пивом и ежегодным празднованием Октоберфеста. Мюнхен является крупным туристическим центром и конференц-центром. Большое значение имеют книгоиздание, полиграфия и телевизионная продукция. Город является центром банковской и финансовой индустрии и имеет один из крупнейших оптовых рынков в Европе для фруктов, овощей и продуктов животного происхождения.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Посмотрите, как строится тоннель метро, ​​чтобы расширить мюнхенскую подземную железнодорожную систему

Посмотреть все видео к этой статье

Мюнхен связан железной дорогой со всеми основными городами Германии и и европейская высокоскоростная пассажирская железнодорожная система. Автобанен (скоростные автомагистрали) из Штутгарта, Нюрнберга и Зальцбурга сходятся в городе. Аэропорт Франца-Иосифа Штрауса, расположенный в 17 милях (27 км) к северо-востоку от Мюнхена, открылся в 1992. В городе построено современное метро.

Старый город, сгруппированный вокруг древнего перекрестка рыночной площади на Мариенплац, все больше становится деловым центром и утратил большую часть своего древнего характера. Среди старых зданий, которые все еще стоят, трое из семи городских ворот — Карловы, Зендлингерские и Изарские, все датируются 14 веком. Другие средневековые здания включают мюнхенский собор, Фрауэнкирхе (церковь Богоматери, построенная в 1468–1488 гг.), чьи массивные башни с куполами являются заметными достопримечательностями; и Старая ратуша (1470–80) на Мариенплац. Рядом находится Петерскирхе (1169 г.), старейшая церковь Мюнхена, которая была полностью разрушена во время Второй мировой войны, но впоследствии восстановлена ​​в своем первоначальном виде. Бывший городской арсенал на Якобсплац теперь является муниципальным музеем.

Самая старая из резиденций Виттельсбахов, Старый двор, сохранила свой средневековый облик. Нынешняя резиденция датируется 16 веком, но стиль каждого периода до 19 века был опробован на ней с превосходным эффектом; здание было разрушено во время Второй мировой войны, но было реконструировано. Еще одним пережитком этого раннего периода является Михаэльскирхе (1583–1599 гг. ).7), которая считается самой важной церковью эпохи Возрождения в Германии и одной из самых красивых в Центральной Европе.

Несмотря на эти старые здания, в старом городе преобладают барокко и рококо. Итальянские модели вдохновили Theatinerkirche конца 17-го века (церковь Theatine), Dreifaltigkeitskirche начала 18-го века (церковь Троицы) и марианскую церковь 18-го века, Bürgersaal. Михаэльскирхе в Берг-ам-Лайме, Асамкирхе (также называемая церковью Св. Иоанна Непомуцкого) и Театр Кувилье в Резиденции были построены между 1746 и 1777 годами. Последняя постройка, великолепный театр в стиле рококо, построенный для двора Виттельсбахов, был разрушен во время Великой Отечественной войны, но большая часть его внутреннего убранства была сохранена, а театр реконструирован. Среди летних замков, построенных за пределами городских стен, можно выделить Шлайсхайм и Нимфенбург. Охотничий домик последнего, Амалиенбургский павильон, является шедевром рококо. Сохранилось также несколько дворцов, построенных одновременно баварской помещичьей и придворной знатью. Новая ратуша (построена в 1867—74) расширена в начале 20 в.

Мюнхен получил первый большой толчок к расширению за пределы старого города благодаря великолепной программе строительства, предпринятой Людовиком I в 19 веке. Между Воротами Победы и Залом генералов он построил монументальную Людвигштрассе, вдоль которой он построил государственную библиотеку, Людвигскирхе и Мюнхенский университет. Другими проектами, заказанными Луи, были Кенигсплац с Глиптотекой («Галерея скульптур»), музеем, в котором хранится коллекция древней и современной скульптуры; Пропилены, великолепные ворота в стиле Пропилей в Афинах; и Старая (Старая) Пинакотека, в которой хранится одна из величайших коллекций картин в Европе. Сын Людовика Максимилиан II (правил в 1848–1864 гг.) построил широкую Максимилиенштрассе и Максимилианеум, в котором сейчас находится баварский парламент (9).0013 Ландтаг ).

Мюнхенский университет был перенесен из Ландсхута в Мюнхен в 1826 году Людовиком I. Среди других важных учебных заведений города Мюнхенский технический университет (основан в 1868 году) и академии искусства, музыки, философии, военных исследований, кино и телевидение. В Мюнхене также находится штаб-квартира Общества содействия развитию науки им. Макса Планка, официальной научно-исследовательской организации Германии.

Мюнхен уже давно является центром искусства. Музыка, особенно опера, процветала. Помимо Баварской государственной оперы, Мюнхенской филармонии и других оркестров существуют Баварская государственная драматическая труппа и многочисленные частные театры. Важные библиотеки включают Баварскую государственную библиотеку и Университетскую библиотеку.

Посмотрите, как серферы занимаются серфингом на реке Айсбах в Мюнхене

Посмотрите все видео к этой статье

Узнайте о мюнхенской резне 1972 года

Посмотрите все видео к этой статье

В Мюнхене есть несколько выдающихся музеев и художественных галерей. В Старой пинакотеке, входящей в состав Баварских государственных картинных галерей, хранятся художественные сокровища, накопленные семьей Виттельсбахов с 16 века. Его коллекции немецких и голландских картин эпохи Возрождения и картин фламандского барокко особенно сильны, со многими шедеврами Альбрехта Дюрера, Питера Пауля Рубенса и Антониса ван Дейка.